Квалиметрия. Контрольная работа по дисциплине Квалиметрия
 Скачать 160 Kb. Скачать 160 Kb.
|
|
Уральский государственный экономический университет Контрольная работа по дисциплине « Квалиметрия » 8 вариант Выполнил: студент гр.УК-10 Ом Огнистов А.Г. Проверила: Михеева С.В ОМСК 2011 Содержание
8 Вариант. Охарактрезуйте требования к эталонным образцам. Методика расчета коэффициэнта конкордации. 1.1Требования к эталонному образцу В общую систему сертификации как на предприятии, так и непосредственно у заказчика могут входить дополнительные требования к эталонному образцу или образцу продукции, с которым впоследствии будут проводиться все сравнения. Цветовой стандарт должен быть тем «идеальным» цветом, к которому мы должны стремиться. Нередки ситуации, когда заказчик передает в типографию образец (оригинал), а затем типография пытается воспроизвести свой собственный «оригинал» с установленными на предприятиями допусками, используя материал, который был на складе. В итоге у заказчика на руках появляются два «эталонных образца», которые близки друг к другу, но не идентичны! Какими же свойствами должен обладать «идеальный оригинал» — эталонный образец? несколько основных свойств: стабильность — то есть реакция оригинала на свет, температуру, время и другие параметры окружающей среды; воспроизводимость — возможно ли воспроизведение эталонного образца каким-либо полиграфическим способом? Подчас эталонный цвет, отпечатанный на немелованной бумаге, пытаются воспроизвести на металлизированной поверхности без наложения кроющих белил, при этом контроль ведется с помощью простых денситометров или спектрофотометров с так называемой линейной оптикой; доступность — если стандартный образец будет утерян, возможна ли его замена и насколько дублер будет приближаться к первому; повторяемость — устойчив ли эталонный цвет от тиража к тиражу, то есть насколько возможно воспроизвести тот же цвет в условиях другой типографии; единообразность — равномерность запечатывания плашки, или на сколько равномерно краска распределилась по поверхности материала — при неравномерном запечатывании речи об инструментальном или даже визуальном контроле быть не может; репрезентативность — насколько цветовой эталон подходит к материалу и структуре материала будущего образца. Выполнение совокупности этих требований будет для заказчика гарантией выпуска качественной продукции на различных предприятиях. 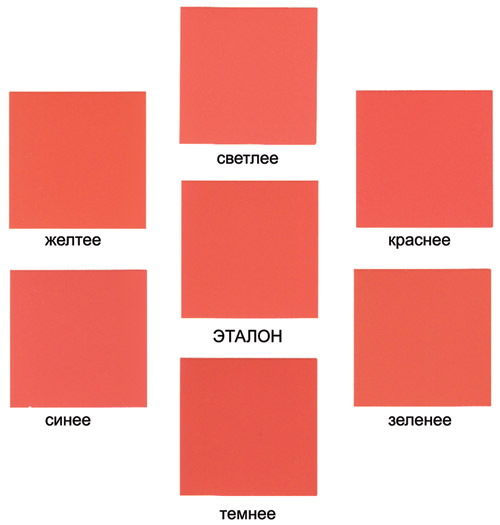 Рис. 2. Физический эталон с возможными цветовыми отклонениями Показательным примером может служить приведенный на рис. 2 некий цветовой стандарт, который, на наш взгляд, наиболее полно определяет совокупность допустимых отклонений при воспроизводстве. Он представляет собой физический образец с возможностью визуального и приборного контроля, отвечающий всем перечисленным выше требованиям. 1.2 Методика расчета коэффициентта конкордации В нечисловой статистике часто возникает необходимость установления степени взаимосвязи (корреляции), или сходства двух, или более объектов. При этом традиционные подходы, основанные на формулах Пирсона, Спирмена и ранговой конкордации Кендалла, часто не дают нужного результата при недостаточной согласованности объектов по одному из измерений и малом объеме исходной выборки (см., например, [1] и [2]). Кроме того, данные формулы требуют предварительной обработки при равенстве рангов объектов. Для решения данной проблемы предлагается использовать модифицированный коэффициент конкордации: 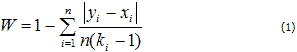 где n - объем выборки, ki - количество признаков по i-му элементу выборки. В случае, когда 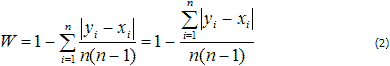 Формула (2) является аналогом коэффициента конкордации Кендалла: но не имеет ограничений, налагаемых на формулу (3). Например, для определения корреляции между результатами, полученными студентами при сдаче экзамена в традиционной форме и в форме компьютерного теста (см. таблицу 1), формула Кендалла требует рангового преобразования пятибалльной (фактически, четырехбалльной, так как оценка 1 не ставится) шкалы оценок с последующим усреднением показателей для равных рангов (см. таблицу 2). Исходные данные. (Таблица 1).
Входные данные для формул Спирмена и Кендалла. (Таблица 1).Студенты 1
Подобные преобразования требуют дополнительных временных затрат, как за счет собственно затрат на преобразования, так и за счет перевода исходных данных в вещественное представление. Модифицированный коэффициент конкордации (1) может работать непосредственно по исходным данным. При этом необходимо либо уменьшить все значения в таблице 1 на единицу, так как мы имеем дело с четырехбалльной шкалой, либо привести (1) к виду: 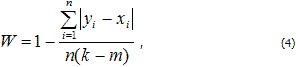 где n - объем выборки, k - максимально возможное значение признака (в нашем случае k=5), m - минимально возможное значение признака (в нашем случае m=2). При этом выполняется интуитивно понятное требование, по которому значение коэффициента конкордации должно быть не меньше, чем 0.8, так как в исходной таблице различаются значения только в двух столбцах из десяти - в первом и пятом (модифицированный коэффициент конкордации, рассчитанный по формуле (4) будет равен 0.9). В то же время, коэффициент конкордации Кендалла, рассчитанный по таблице 2 и формуле (3), будет приблизительно равен 0.64, что, с точки зрения статистики, является достаточно плохим результатом, практически говорящим об отсутствии связи между данными, полученными с помощью тестирования и экзамена. Литература 1.Красильников В.В. Статистика объектов нечисловой природы. Набережные Челны, изд-во Камского политехнического института, 2001 г., 144 с. 2.Орлов А.И. Нечисловая статистика. М.: "МЗ-Пресс", 2004 г., 516 с. |
