контольная работа по матзадачи. Матзадачи и компмоделиров в ЭЭ. Контрольная работа по дисциплине Математические задачи и компьютерное моделирование в электроэнергетике
 Скачать 110.42 Kb.
|
|
Министерство образования и науки Республики Казахстан южно-казахстанский университет им.м.ауЭзова Кафедра «Энергетика и нетрадиционные энергетические системы»  Контрольная работапо дисциплине «Математические задачи и компьютерное моделирование в электроэнергетике» Выполнил: студент группы ЗИП-20-4ру Каримов Ш.К. Принял: Файз Н.С. Шымкент, 2021 Задание №1 1.Вычислить определитель квадратной матрицы A 3 порядка 2 способами: Дано: A= 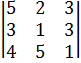 .1 Классический способ: 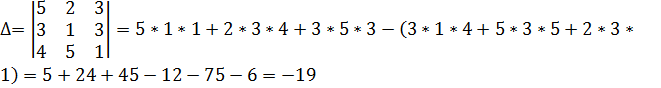 .2 Путем разложения определителя по столбцу или строке: Расчет проводим по разложению 1-ой строки. 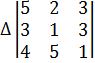 = 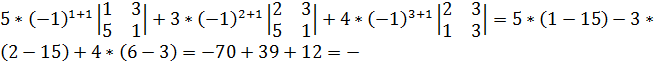19. Найти определитель матрицы А в системе MATLAB. >> a=[5 2 3; 3 1 3; 4 5 1]= 2 3 1 3 5 1 >> det(a) ans = -19 . Найти обратную матрицу матрицы A классическим способом. A= 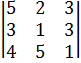;  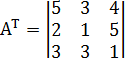Заменим каждый элемент определителем, полученным при вычеркивании соответствующей строки и столбца: 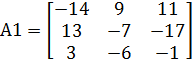  15= - 13        Поменяем знаки у элементов с нечетной суммой индексов: 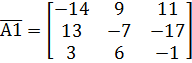 Разделим все элементы матрицы 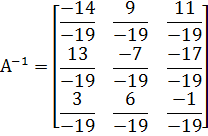 на определитель ∆= - 19. В результате получим обратную матрицу: .Вычислить обратную матрицу матрицы А в системе MATLAB: >> a= [5 2 3; 3 1 3; 4 5 1]= 2 3 1 3 5 1 >> inv(a)= .7368 -0.6842 -0.1579 .4737 0.3684 0.3158 .5789 0.8947 0.0526 Задание №2 Для схемы представленной на рисунке 2 найти токи в ветвях разомкнутой электрической сети, используя матричную форму записи 1-го закона Кирхгофа. 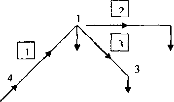 Рис. 2 Токи нагрузки узлов равны: 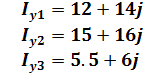 Матрица задающих токов принимает вид: 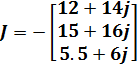 Матрица токов равна матрице токов нагрузок, взятой с противоположным знаком. Выберем в качестве балансирующего узла- узел 4. 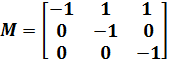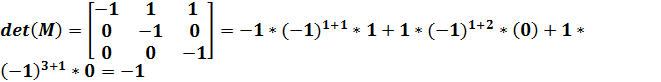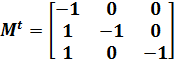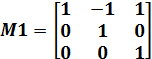Обозначим через М матрицу инциденций без балансирующего узла:  , вычисли обратную матрицу классическим методом:Определитель матрицы   , заменим каждый элемент определителем, полученным при вычеркивании соответствующей строки и столбца:          Поменяем знаки у элементов с нечетной суммой индексов: 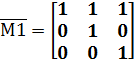 Разделим все элементы матрицы 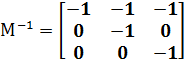на определитель ∆=-1. В результате получим обратную матрицу: Из обобщенного уравнения состояния, токи в ветвях: 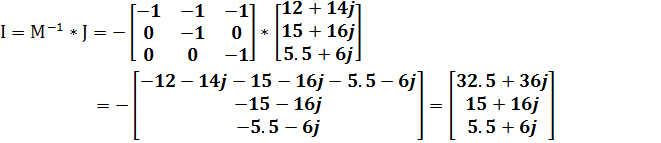 Проделаем то же самое с помощью MATLAB: Первая матрица инциденций: >> M=[-1 1 1;0 -1 0;0 0 -1]= 1 1 -1 0 0 -1 Обратная матрица матрицы М: >> inv(M)= -1 -1 -1 0 0 -1 Матрица задающих токов: >> J=-[12+14i;15+16i;5.5+6i] = .0000 -14.0000i .0000 -16.0000i .5000 - 6.0000i Токи в ветвях: >> I=inv(M)*J I = .5000 +36.0000i .0000 +16.0000i .5000 + 6.0000i Ответ: Токи в ветвях вычисленные аналитически равны I 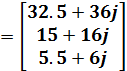 ,с помощью MATLAB I = 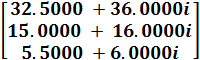 |