Контрольная работа по дисциплине Методы оптимальных решений часть 1 (название дисциплины)
 Скачать 392.5 Kb. Скачать 392.5 Kb.
|
|
Оптимальный план двойственной задачи равен: y1 = 15, y2 = 5, y3 = 0 Z(Y) = 4800*15+2400*5+1500*0 = 84000 Задание 3 Решить транспортную задачу с использованием вычислительных средств Excel. Имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i- го пункта производства в j-й центр распределения Сij приведена в таблице, где под строкой понимается пункт производства, а под столбцом - пункт распределения. Кроме того, в этой таблице в i-й строке указан объем производства в i- м пункте производства, а в j-м столбце указан спрос в j-м центре распределения. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы. 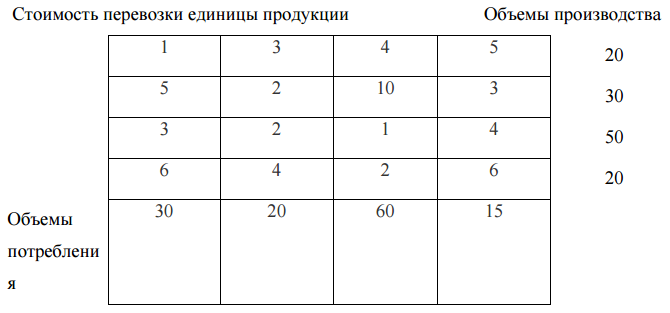 Решение  Решение 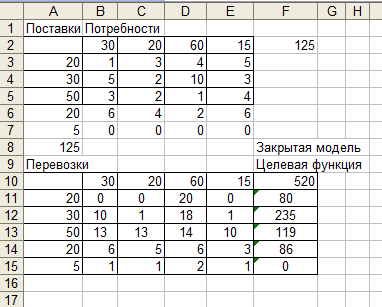 Задание 4 Решить задачу о назначениях преподавателей на проведение занятий в соответствии с заданной таблицей. 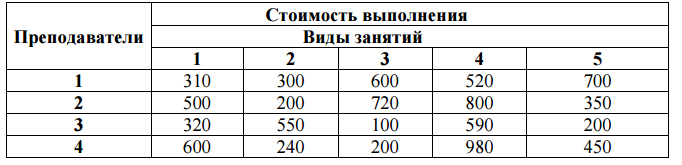 Решение Для устранения дисбаланса добавляем дополнительные строки. 1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.
Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент.
После вычитания минимальных элементов получаем полностью редуцированную матрицу. 2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость. Фиксируем нулевое значение в клетке (1, 2). Другие нули в строке 1 и столбце 2 вычеркиваем. Для данной клетки вычеркиваем нули в клетках (2; 2), (5; 2) В итоге получаем следующую матрицу:
Поскольку расположение нулевых элементов в матрице не позволяет образовать систему из 5-х независимых нулей (в матрице их только 1), то решение недопустимое. 3. Проводим модификацию матрицы. Вычеркиваем строки и столбцы с возможно большим количеством нулевых элементов: строку 5, столбец 2, столбец 3 Получаем сокращенную матрицу (элементы выделены):
Минимальный элемент сокращенной матрицы (min(10, 220, 400, 300, 600, 150, 220, 490, 100, 400, 780, 250) = 10) вычитаем из всех ее элементов:
Затем складываем минимальный элемент с элементами, расположенными на пересечениях вычеркнутых строк и столбцов:
1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль. Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент. После вычитания минимальных элементов получаем полностью редуцированную матрицу. 2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость. Фиксируем нулевое значение в клетке (1, 2). Другие нули в строке 1 и столбце 2 вычеркиваем. Для данной клетки вычеркиваем нули в клетках (2; 2), (1; 1). В итоге получаем следующую матрицу:
Поскольку расположение нулевых элементов в матрице не позволяет образовать систему из 5-х независимых нулей (в матрице их только 1), то решение недопустимое. 3. Проводим модификацию матрицы. Вычеркиваем строки и столбцы с возможно большим количеством нулевых элементов: строку 5, столбец 2, столбец 3, строку 1 Получаем сокращенную матрицу (элементы выделены):
|
