Контрольная работа по дисциплине Методы оптимальных решений часть 1 (название дисциплины)

• Название: Контрольная работа по дисциплине Методы оптимальных решений часть 1 (название дисциплины)
• Дата: 02.11.2018
• Размер: 392.5 Kb.
• Имя файла: zadachi_1.doc
• Тип: Контрольная работа; #55227
• страница: 2 из 4

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x₃, так как это наибольший коэффициент по модулю.
Вычислим значения D_i по строкам как частное от деления: b_i / a_i3
и из них выберем наименьшее:
min (8⁴/₁₃ : ³/₁₃ , 86¹²/₁₃ : 1⁹/₁₃ , 7⁹/₁₃ : ¹⁰/₁₃ ) = 10
Следовательно, 3-ая строка является ведущей.
Разрешающий элемент равен (¹⁰/₁₃) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	x7	min
x5	108/13	9/13	7/13	3/13	0	1	0	-1/13	36
x6	1130/13	66/13	47/13	22/13	0	0	1	-3/13	565/11
x4	100/13	4/13	6/13	10/13	1	0	0	1/13	10
F(X2)	1000	-20	-10	-20	0	0	0	10

Формируем следующую часть симплексной таблицы. Вместо переменной x₄ в план 2 войдет переменная x₃.
Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7
x5	6	3/5	2/5	0	-3/10	1	0	-1/10
x6	70	22/5	13/5	0	-11/5	0	1	-2/5
x3	10	2/5	3/5	1	13/10	0	0	1/10
F(X2)	1200	-12	2	0	26	0	0	12

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.
Вычислим значения D_i по строкам как частное от деления: b_i / a_i1
и из них выберем наименьшее:
min (6 : ³/₅ , 70 : 4²/₅ , 10 : ²/₅ ) = 10
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (³/₅) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	x7	min
x5	6	3/5	2/5	0	-3/10	1	0	-1/10	10
x6	70	22/5	13/5	0	-11/5	0	1	-2/5	175/11
x3	10	2/5	3/5	1	13/10	0	0	1/10	25
F(X3)	1200	-12	2	0	26	0	0	12

Формируем следующую часть симплексной таблицы. Вместо переменной x₅ в план 3 войдет переменная x₁.
Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6	x7
x1	10	1	2/3	0	-1/2	5/3	0	-1/6
x6	26	0	-1/3	0	0	-22/3	1	1/3
x3	6	0	1/3	1	3/2	-2/3	0	1/6
F(X3)	1320	0	10	0	20	20	0	10

Конец итераций: индексная строка не содержит отрицательных элементов - найден оптимальный план
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5	x6	x7
x1	10	1	2/3	0	-1/2	5/3	0	-1/6
x6	26	0	-1/3	0	0	-22/3	1	1/3
x3	6	0	1/3	1	3/2	-2/3	0	1/6
F(X4)	1320	0	10	0	20	20	0	10

Оптимальный план можно записать так:

x₁ = 10, x₂ = 0, x₃ = 6, x₄ = 0

F(X) = 60•10 + 70•0 + 120•6 + 130•0 = 1320

Задание 2

Построить математическую модель задачи. Составить задачу, двойственную к исходной. Исходя из специализации и своих технологических возможностей, предприятие может выпускать 4 вида продукции. Сбыт любого количества обеспечен. Для изготовления этой продукции используется трудовые ресурсы, полуфабрикаты и станочное оборудование. Общий объем ресурсов (в расчете на трудовую неделю), расход каждого ресурса на единицу выпускаемой продукции и цена, полученная за единицу продукции, приведены в таблице. Требуется определить план выпуска, доставляющий предприятию максимум выручки.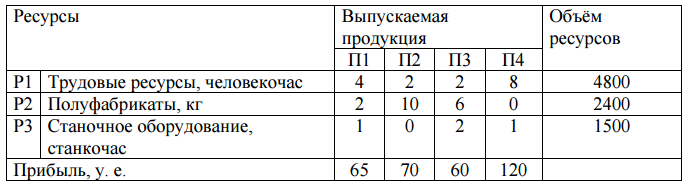



Решение

Определим максимальное значение целевой функции F(X) = 65x1+70x2+60x3+120x4 при следующих условиях-ограничений.

4x1+2x2+2x3+8x4≤4800

2x1+10x2+6x3≤2400

x1+2x3+x4≤1500

Неравенства, соединенные стрелочками (↔), называются сопряженными.
4y₁+2y₂+y₃≥65
2y₁+10y₂≥70
2y₁+6y₂+2y₃≥60
8y₁+y₃≥120
4800y₁+2400y₂+1500y₃ → min
y₁ ≥ 0
y₂ ≥ 0
y₃ ≥ 0

Исходная задача I		Двойственная задача II
x1 ≥ 0	↔	4y1+2y2+y3≥65
x2 ≥ 0	↔	2y1+10y2≥70
x3 ≥ 0	↔	2y1+6y2+2y3≥60
x4 ≥ 0	↔	8y1+y3≥120
65x1+70x2+60x3+120x4 → max	↔	4800y1+2400y2+1500y3 → min
4x1+2x2+2x3+8x4≤4800	↔	y1 ≥ 0
2x1+10x2+6x3≤2400	↔	y2 ≥ 0
x1+2x3+x4≤1500	↔	y3 ≥ 0

Решение двойственной задачи дает оптимальную систему оценок ресурсов.
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
Из теоремы двойственности следует, что Y = C*A^-1.
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

A = (A4, A3, A7) =

8 2 0 0 6 0 1 2 1

Определив обратную матрицу D = А^-1 через алгебраические дополнения, получим:

D = A-1 =

1/8 -1/24 0 0 1/6 0 -1/8 -7/24 1

Как видно из последнего плана симплексной таблицы, обратная матрица A^-1 расположена в столбцах дополнительных переменных.
Тогда Y = C*A^-1 = 

(120, 60, 0) x

1/8 -1/24 0 0 1/6 0 -1/8 -7/24 1

= (15;5;0)