математическое моделирование. 8806482_Оптимальные_решения. Контрольная работа по дисциплине Методы оптимальных решений вариант 8 Выполнил(а) студент Ф. И. О. по направлению
 Скачать 65.22 Kb. Скачать 65.22 Kb.
|
ТЕМА 4 ПРИНЯТИЕ РЕШЕНИЙ НА ОСНОВЕ ТЕОРИИ ИГРМинистерство желает построить один из двух объектов на территории города. Городские власти могут принять предложение министерства или отказать. Министерство — первый игрок — имеет две стратегии: строить 1-йобъект, строить 2-й объект. Город — второй игрок — имеет две стратегии: принять предложение министерства или отказать. Свои действия (стратегии) они применяют независимо друг от друга, и результаты определяются прибылью (выигрышем) согласно следующим матрицам: Вариант 38 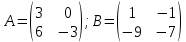 (например, если игроки применяют свои первые стратегии, министерство решает строить 1 объект, а городские власти разрешают его постройку, тогда город получает выигрыш 1 млн, а министерство получает выигрыш 3 млн, и т.д.) Решение: В каждом столбце матрицы A найдем максимальный элемент. Эти элементы подчеркнуты в матрице A. Их положение соответствует приемлемым ситуациям 1-го игрока, когда второй игрок выбрал стратегию j соответственно. Затем в каждой строке матрицы B выберем наибольший элемент. Эти элементы подчеркнуты в матрице B. Их положение будет определять приемлемые ситуации 2-го игрока, когда первый игрок выбрал стратегию i соответственно. Платежная матрица игрока А:
Позиции максимумов в столбцах матрицы А: (2,1), (1,2) Платежная матрица игрока B:
Позиции максимумов в строках матрицы В: (1,1), (2,2) Если биматричная игра не имеет равновесных ситуаций в чистых стратегиях, то она неразрешима в чистых стратегиях. И тогда можно искать решение в смешанных стратегиях. Итак, чтобы в биматричной игре: А=(a), В = (b) пара (p,q); определяемая равновесную ситуацию, необходимо и достаточно одновременное выполнение следующих неравенств: (p–1)(Cq-α) ≥ 0, p(Cq-α) ≥ 0; 0 ≤ p ≤ 1 (q-1)(Dp-β) ≥ 0, q(Dp-β) ≥ 0; 0 ≤ q ≤ 1 где C = a11 - a12 - a21 + a22 α = a22- a12 D = b11-b12-b21+b22 β = b22-b21 Проводя необходимые вычисления: C = 3 - 0 - 6 -3 = -6 α = -3 - 0 = -3 D = 1 - (-1) - (-9) -7 = 4 β = -7 - (-9) = 2 и рассуждения (p–1)(-6q+3) ≥ 0 p(-6q+3) ≥ 0 (q-1)(4p-2) ≥ 0 q(4p-2) ≥ 0 получаем, что: 1) p=1,q ≤ 1/2 p=0, q ≥ 1/2 0 ≤ p ≤ 1, q=1/2 2) q=1,p ≥ 1/2 q=0, p ≤ 1/2 0 ≤ q ≤ 1, p=1/2 Рассматриваемая игра имеет единственную ситуацию равновесия (P*,Q*), где оптимальными стратегиями по Нэшу являются: P* = (1/2;1/2); Q* = (1/2;1/2). Она может быть реализована при многократном повторении игры (то есть при многократном воспроизведении описанной ситуации) следующим образом: игрок I должен использовать чистые стратегии 1 и 2 с частотами 1/2 и 1/2, а игрок II – чистые стратегии 1 и 2 с частотами 1/2 и 1/2. Любой из игроков, отклонившись от указанной смешанной стратегии, уменьшает свой ожидаемый выигрыш. Цена игры Н1 = 6/0,25 = 24 Н2 = -16/0,25 = -64 Цена игры для первого игрока: Ha(1/2;1/2) = 24 Цена игры для второго игрока: Hb(1/2;1/2) = -64 Ответ: Смешанная стратегия для первого игрока P* = (1/2;1/2); Смешанная стратегия для второго игрока Q* = (1/2;1/2). Выигрыш игроков в равновесной ситуации: f(P*,Q*) = (24;-64). Ответ: Смешанная стратегия для первого игрока P* = (1/2;1/2); Смешанная стратегия для второго игрока Q* = (1/2;1/2). Выигрыш игроков в равновесной ситуации: f(P*,Q*) = (24;-64). Т.е. министерство должно с примерно равным энтузиазмом настаивать на строительстве любого объекта. Город должен сопротивляться строительству любого объекта. |
