математическое моделирование. 8806482_Оптимальные_решения. Контрольная работа по дисциплине Методы оптимальных решений вариант 8 Выполнил(а) студент Ф. И. О. по направлению
 Скачать 65.22 Kb.
|
ТЕМА 3. ПРИНЯТИЯ РЕШЕНИЙ В ЗАДАЧАХ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.Для производства трех видов продукции A, B, C используется три вида сырья I, II, III. Нормы затрат каждого из видов сырья на единицу продукции каждого вида, а также прибыль с единицы продукции приведены в таблице. Вариант 28
Определить план выпуска продукции для получения максимальной прибыли при условии, что сырье III должно быть полностью израсходовано. 1. Построить математическую модель задачи. 2. Привести задачу к стандартной форме. 3. Решить полученную задачу графическим методом. 4. Привести задачу к канонической форме. 5. Решить полученную задачу симплекс-методом. 6. Провести анализ модели на чувствительность. 7. Проанализировать результаты решения. Решение 1) Обозначим: x1 - план выпуска продукции А; x2 - план выпуска продукции В; x3 - план выпуска продукции С. Целевая функция (требование максимальной прибыли): F(X) = 6x1+9x2+1x3 → max 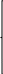 Ограничения по запасам сырья:4x1+12x2+1x3 ≤ 64 6x1+8x2+1x3 ≤ 64 2x1+4x2+1x3 = 24 x1,x2,x3 ≥ 0 2) Приведем задачу к стандартной форме, т.е. к виду, где все ограничения имеют форму неравенств. Выразим из третьего ограничения-уравнения одну из переменных, например, x3: x3 = 24-2x1-4x2 Подставим полученное выражение для х3 в целевую функцию и оставшиеся ограничения, получим задачу в стандартной форме: 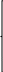 F(X) = 4x1+5x2+24 → max2x1+8x2 ≤ 40 4x1+4x2 ≤ 40 x1+2x2 ≤ 12 x1, x2 ≥ 0 3) 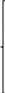 Необходимо найти максимальное значение целевой функции F = 4x1+5x2+24 → max, при системе ограничений: x1+4x2≤20 (1) x1+x2≤10 (2) x1+2x2≤12 (3) x1 ≥ 0 (4) x2 ≥ 0 (5) Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений ABCDE. 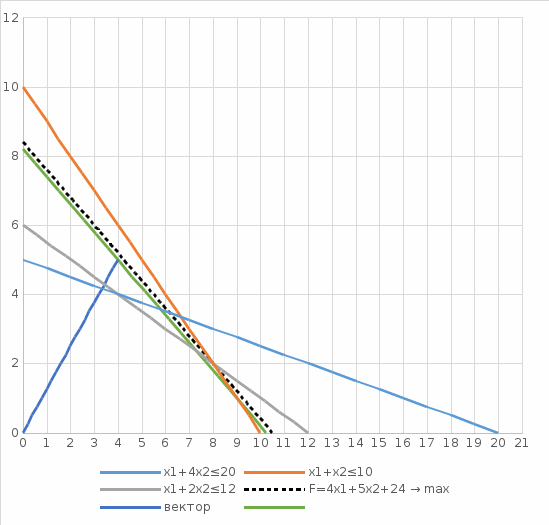 Рассмотрим целевую функцию задачи F = 4x1+5x2+24 → max. Построим прямую, отвечающую значению функции F = 4x1+5x2+24 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (4;5). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией. Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых: x1+x2=10 x1+2x2=12 Решив систему уравнений, получим: x1 = 8, x2 = 2 Откуда найдем максимальное значение целевой функции: F(x) = 4*8 + 5*2 + 24 = 66 F(X) = 2*2 + 3*4 + 12 = 28 4)-5) Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.  Определим максимальное значение целевой функции F(X) = 6x1+9x2+x3 при следующих условиях-ограничений. 4x1+12x2+x3≤64 6x1+8x2+x3≤64 2x1+4x2+x3≤24 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6.  4x1+12x2+x3+x4 = 64 6x1+8x2+x3+x5 = 64 2x1+4x2+x3+x6 = 24 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: Решим систему уравнений относительно базисных переменных: x4, x5, x6 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,64,64,24) Базисное решение называется допустимым, если оно неотрицательно.
Переходим к основному алгоритму симплекс-метода. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: min (64 : 12 , 64 : 8 , 24 : 4 ) = 5.333 Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен (12) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x4 в план 1 войдет переменная x2. Строка, соответствующая переменной x2 в плане 1, получена в результате деления всех элементов строки x4 плана 0 на разрешающий элемент РЭ=12. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Таким образом, в новом плане 1 заполнены строка x2 и столбец x2. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А*В)/РЭ СТЭ - элемент старого плана, РЭ - разрешающий элемент (12), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai1 и из них выберем наименьшее: min (5.333 : 0.333 , 21.333 : 3.333 , 2.667 : 0.667 ) = 4 Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (0.667) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x6 в план 2 войдет переменная x1. Строка, соответствующая переменной x1 в плане 2, получена в результате деления всех элементов строки x6 плана 1 на разрешающий элемент РЭ=0.667. На месте разрешающего элемента получаем 1. В остальных клетках столбца x1 записываем нули. Таким образом, в новом плане 2 заполнены строка x1 и столбец x1. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника. Получаем новую симплекс-таблицу:
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x4, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai4 и из них выберем наименьшее: min (4 : 0.25 , 8 : 1 , - ) = 8 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (1) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 3 войдет переменная x4. Строка, соответствующая переменной x4 в плане 3, получена в результате деления всех элементов строки x5 плана 2 на разрешающий элемент РЭ=1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x4 записываем нули. Таким образом, в новом плане 3 заполнены строка x4 и столбец x4. Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника. Получаем новую симплекс-таблицу:
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 8, x2 = 2, x3 = 0 F(X) = 6*8 + 9*2 + 1*0 = 66 6)-7) Анализ оптимального плана. В оптимальный план вошла дополнительная переменная x4. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 2-го вида в количестве 8. Значение 0 в столбце x1 означает, что использование x1 - выгодно. Значение 0 в столбце x2 означает, что использование x2 - выгодно. Значение 0.5> 0 в столбце x3 означает, что использование x3 - не выгодно. Значение 0 в столбце x4 означает, что теневая цена (двойственная оценка) равна y1=0. Значение 0.75 в столбце x5 означает, что теневая цена (двойственная оценка) равна y2=0.75. Значение 0.75 в столбце x6 означает, что теневая цена (двойственная оценка) равна y3=0.75. Анализ устойчивости оптимального плана. Проведем анализ устойчивости оптимального плана и оценим степень влияния изменения ресурсов на значение целевой функции. Чувствительность решения к изменению коэффициентов целевой функции. Так как любые изменения коэффициентов целевой функции оказывают влияние на оптимальность полученного ранее решения, то наша цель - найти такие диапазоны изменения коэффициентов в целевой функции (рассматривая каждый из коэффициентов отдельно), при которых оптимальные значения переменных остаются неизменными. Пусть каждое значение параметра целевой функции изменится на ∆ сi. Найдем интервалы, при которых будет экономически выгодно использование ресурсов. Допустимые диапазоны изменения коэффициентов в целевой функции определятся из соотношений: 1-й параметр целевой функции может изменяться в пределах: ∆c1- = min [yk/d1k] для d1k>0. ∆c1+ = |max[yk/d1k]| для d1k<0. где в знаменателе коэффициенты столбцов свободных переменных в оптимальном плане (коэффициенты структурных сдвигов, элементы обратной матрицы к базису оптимального плана). Таким образом, 1-й параметр может быть уменьшен на 1.5 или увеличен на 0.75. Интервал изменения равен: (c1 - ∆c-1; c1 + ∆c1+) [6-1.5; 6+0.75] = [4.5;6.75] Если значение c1 будет лежать в данном интервале, то оптимальный план не изменится. 2-й параметр целевой функции может изменяться в пределах: ∆c2- = min [yk/d2k] для d2k>0. ∆c2+ = |max[yk/d2k]| для d2k<0. Таким образом, 2-й параметр может быть уменьшен на 1 или увеличен на 3. Интервал изменения равен: (c2 - ∆c-2; c2 + ∆c2+) [9-1; 9+3] = [8;12] Если значение c2 будет лежать в данном интервале, то оптимальный план не изменится. Верхняя граница для: ∆c3+ ∆c3+ = |max[yk/dk3]| для dk3<0. Таким образом, 3-й коэффициент может быть увеличен на 0.75. ∆c3- = +∞ Интервал изменения равен: (c3 - ∆c3-; +∞) [1-∞;1+0.75] = [-∞;1.75] Чувствительность решения к изменению запасов сырья. Из теоремы об оценках известно, что колебание величины bi приводит к увеличению или уменьшению F(X). Оно определяется величиной yi в случае, когда при изменении величин bi значения переменных уi в оптимальном плане соответствующей двойственной задачи остаются неизменными. Поэтому необходимо найти такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, в которых оптимальный план двойственной задачи не менялся бы. Найдем интервалы устойчивости ресурсов. Нижняя граница для: ∆b1- ∆b1- = min[xk/dk1] для dk1>0. Таким образом, 1-й запас может быть уменьшен на 8. 1-й вид ресурса в оптимальном плане недоиспользован, является недефицитным. Увеличение данного ресурса приведет лишь к росту его остатка. При этом структурных изменений в оптимальном плане не будет, так как двойственная оценка y1 = 0. Другими словами, верхняя граница b1+ = +∞ ∆b1+ = +∞ Интервал изменения равен: (b1 - ∆b1-; +∞) [64-8; +∞] = [56;+∞] 2-й запас может изменяться в пределах: ∆b2- = min[xk/dk2] для dk2>0. ∆b2+ = |max[xk/dk2]| для dk2<0. Таким образом, 2-й запас может быть уменьшен на 8 или увеличен на 8. Интервал изменения равен: (b2 - ∆b2-; b2 + ∆b2)+ [64-8; 64+8] = [56;72] 3-й запас может изменяться в пределах: ∆b3- = min[xk/dk3] для dk3>0. ∆b3+ = |max[xk/dk3]| для dk3<0. Таким образом, 3-й запас может быть уменьшен на 2.667 или увеличен на 1.6. Интервал изменения равен: (b3 - ∆b3-; b3 + ∆b3)+ [24-2.667; 24+1.6] = [21.333;25.6] В оптимальный план не вошла основная переменная x1, т.е. ее не выгодно использовать. Определим максимально возможное значение в рамках полученных двойственных оценок: x1 может изменяться в пределах: 0 ≤ x1 ≤ 8 Ответ: Для получения максимальной прибыли = 66 ед. при заданных граничных мы должны производить 8 ед. продукции А и 2 ед. продукции В. Продукцию С производить невыгодно. При реализации такого плана производства имеются недоиспользованные ресурсы 1-го вида в количестве 8. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||