математическое моделирование. 8806482_Оптимальные_решения. Контрольная работа по дисциплине Методы оптимальных решений вариант 8 Выполнил(а) студент Ф. И. О. по направлению
 Скачать 65.22 Kb. Скачать 65.22 Kb.
|
ТЕМА 5. ПРИНЯТИЕ РЕШЕНИЙ НА ОСНОВЕ БАЛАНСОВОЙ МОДЕЛИРассматривается двухотраслевая модель экономики. Задана балансовая таблица за прошедший год.
1. Найдите валовой выпуск каждой отрасли в прошедшем году; запишите вектор валового выпуска 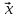 для прошедшего года. для прошедшего года. 2. Найдите матрицу Леонтьева A. Сделать проверку продуктивности матрицы прямых затрат. 3. Найдите матрицу полных затрат B. 4. В следующем году конечное потребление продукции отрасли I увеличится на a%, а отрасли II - уменьшится на b%. a = 20% b = 10% Найдите конечное потребление продукции каждой отрасли в следующем году. Запишите вектор конечного потребления 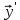 для следующего года. для следующего года. 5. Найдите валовой выпуск каждой отрасли в следующем году; запишите вектор валового выпуска 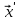 для следующего года. для следующего года. 6. На сколько процентов изменился валовой выпуск каждой отрасли в следующем году по сравнению с прошедшим? 7. Известен вектор норм добавленной стоимости 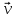 в прошедшем году. в прошедшем году. 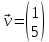 Найдите равновесные цены продукции каждой отрасли в прошедшем году. Запишите вектор равновесных цен 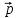 8. На основании расчетов п.4-7, принятии решение: стоит или нет увеличивать конечное потребление продукции каждой отрасли. 9. Что показывает равновесная цена. Как данная цена влияет на принятия решения по увеличению конечного потребления продукции. Решение Так как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями и конечного продукта, то: xi = (xi1 + xi2 + ... + xin) + yi, (i = 1,2,...,n). Эти уравнения (их n штук) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в эти уравнения, имеют стоимостное выражение. Введем коэффициенты прямых затрат: aij = xij/xj, (i,j = 1,2,...,n), показывающие затраты продукции i-й отрасли на производство единицы стоимости j-й отрасли. Находим валовой объем продукции xi; x1 = 2 + 2 + 3 = 7 x2 = 3 + 7 + 7 = 17 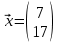
По формуле aij = xij / xj находим коэффициенты прямых затрат: a11 = 2/7 = 0.286; a12 = 2/17 = 0.118; a21 = 3/7 = 0.429; a22 = 7/17 = 0.412;
Коэффициент прямых затрат (aij) показывает, какое количество продукции i-й отрасли необходимо, учитывая только прямые затраты, для производства единицы продукции j-й отрасли. Критерии продуктивности матрицы А Существует несколько критериев продуктивности матрицы А. 1. Матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы. 2. Для того чтобы обеспечить положительный конечный выпуск по всем отраслям необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий: 3. Определитель матрицы (E - A) не равен нулю, т.е. матрица (E- A) имеет обратную матрицу (E - A)-1. 4. Наибольшее по модулю собственное значение матрицы А, т.е. решение уравнения |λE - A| = 0 строго меньше единицы. 5. Все главные миноры матрицы (E - A) порядка от 1 до n, положительны. Матрица A имеет неотрицательные элементы и не удовлетворяет критерию продуктивности (сумма элементов второго столбца ∑ai2 > 1. Коэффициент полных затрат (bij) показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли. Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства продукции. а) Находим матрицу (E-A):
б) Вычисляем обратную матрицу (E-A)-1: Запишем матрицу в виде: Главный определитель ∆=(0.71•0.59-(-0.43•(-0.12)))=0.36974789915966 Определитель отличен от нуля, следовательно, матрица является невырожденной и для нее можно найти обратную матрицу B-1. Транспонированная матрица. Найдем алгебраические дополнения матрицы BT. BT11=(-1)1+10.588=0.588; BT12=(-1)1+2-0.118=0.118; BT21=(-1)2+1-0.429=0.429; BT22=(-1)2+20.714=0.714; Обратная матрица. Составим систему балансовых уравнений: x1-(0.286x1+0.118x2)=y1 x2-(0.429x1+0.412x2)=y2 или 0.714x1-0.118x2=y1 -0.429x1+0.588x2=y2 Элементы каждого столбца bij показывают, сколько нужно затратить продукции каждой отрасли для производства только единицы конечного продукта j-й отрасли. Найдем величины валовой продукции 2-х отраслей = Межотраслевой баланс состоит из четырех квадрантов (табл. ниже). Первый квадрант отражает межотраслевые потоки продукции. Второй характеризует отраслевую материальную структуру национального дохода. Третий представляет национальный доход как стоимость условно-чистой продукции (Zj), равной сумме амортизации (cj), оплаты труда (vj) и чистого дохода j-й отрасли (mj). Четвертый квадрант показывает конечное распределение и использование национального дохода. Составляющие третьего квадранта (условно-чистая продукция) находятся как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта: Zj = Xj - ∑xij Величина условно чистой продукции Zi равна сумме амортизации, оплаты труда и чистого дохода отрасли j. 7 - (2 + 3) = 2 17 - (2 + 7) = 8 Межотраслевые поставки продукции: 0.2857*7=2; 0.1176*17=2; 0.4286*7=3; 0.4118*17=7;
Проверим основное балансовое соотношение по формуле основного балансового соотношения ∑yi = ∑zj = 10 В следующем году конечное потребление продукции отрасли I увеличится на 20%, а отрасли II - уменьшится на 10%. Вектор конечного потребления 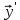 для следующего года. для следующего года. 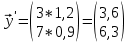 Вектор валового выпуска 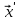 для следующего года. для следующего года.
Валовой выпуск каждой отрасли в следующем году по сравнению с прошедшим изменился на: 1-ой – 7,732/7 = 1,1 = 10% - вырос на 10% 2-ой – 16,343/17 = 0,96 = -4% - сократился на 4% Вектор норм добавленной стоимости 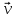 в прошедшем году. в прошедшем году. 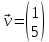 Равновесные цены продукции каждой отрасли в прошедшем году найдем с помощью «двойственного» уравнения Леонтьева 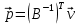
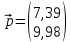 Модель равновесных цен позволяет, зная величины норм добавленной стоимости, прогнозировать цены на продукцию отраслей. Набор цен при котором прибыль каждого объекта равна нулю, в том случае, когда уровень зарплаты позволяет приобрести весь конечный продукт системы называется равновесным. Ответ вектор валового выпуска 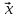 для прошедшего года для прошедшего года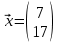 матрица прямых затрат
матрица полных затрат
вектор конечного потребления 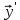 для следующего года для следующего года 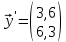 запишите вектор валового выпуска 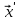 для следующего года для следующего года
процент изменения валового выпуска каждой отрасли в следующем году по сравнению с прошедшим 1-ой – вырос на 10% 2-ой – сократился на 4% вектор равновесных цен 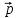 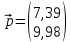 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
