методы прогнозирования территорий. Контрольная работа по дисциплине "Методы прогнозирования территорий"
 Скачать 184 Kb.
|
|
Контрольная работа по дисциплине "Методы прогнозирования территорий" Задание. Имеются данные, характеризующие уровень безработицы в регионе, % Уровень безработицы
1. Постройте прогноз уровня безработицы в регионе на ноябрь, декабрь, январь месяцы, используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов. 2. Постройте график фактических и расчетных показателей. 3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода. 4. Сравните полученные результаты, сделайте вывод. Решение. 1. Одним из наиболее старых и широко известных методов сглаживания временных рядов является метод скользящих средних. Применяя этот метод, можно элиминировать случайные колебания и получить значения, соответствующие влиянию главных факторов. Сглаживание с помощью скользящих средних основано на том, что в средних величинах взаимно погашаются случайные отклонения. Это происходит вследствие замены первоначальных уровней временного ряда средней арифметической величиной внутри выбранного интервала времени. Полученное значение относится к середине выбранного периода. Затем период сдвигается на одно наблюдение, и расчет средней повторяется, причем периоды определения средней берутся все время одинаковыми. Таким образом, в каждом случае средняя центрирована, т.е. отнесена к серединной точке интервала сглаживания и представляет собой уровень для этой точки. Рабочая формула имеет вид:  =  +  если  где t + 1 – прогнозный период; t – период, предшествующий прогнозному периоду (год, месяц и т.д.); yt+1 – прогнозируемый показатель;  – скользящая средняя за два периода до прогнозного; n – число уровней, входящих в интервал сглаживания; yt– фактическое значение исследуемого явления за предшествующий период; yt-1 – фактическое значение исследуемого явления за два периода, предшествующих прогнозному. Рассчитаем скользящую среднюю для первых трех периодов: mфев = (Yянв + Yфев + Yмарт)/ 3 = (2,99+2,66+2,63)/3 = 2,76. Полученное значение заносим в таблицу в средину взятого периода. Далее рассчитываем m для следующих трех периодов февраль, март, апрель: mмарт = (Yфев + Yмарт + Yапр)/ 3 = (2,66+2,63+2,56)/3 = 2,62. В соответствие с приведенной выше формулой строим прогноз: Yноябрь = 1,57 + 1/3 (1,42 – 1,56) = 1,57 – 0,05 = 1,52 Определяем скользящую среднюю m для октября: m = (1,56+1,42+1,52) /3 = 1,5. Строим прогноз на декабрь: Yдекабрь = 1,5 + 1/3 (1,52 – 1,42) = 1,53 Определяем скользящую среднюю m для ноября: m = (1,42+1,52+1,53)/3 = 1,49. Строим прогноз на январь: Yянварь = 1,49 + 1/3 (1,53 – 1,52) = 1,49. Прогнозирование на основе метода экспоненциального сглаживания наиболее эффективно при разработке среднесрочных прогнозов. Основные достоинства метода: простота процедура вычислений; возможность учета весов исходной информации. Рабочая формула метода экспоненциального сглаживания:  где t – период, предшествующий прогнозному; t+1– прогнозный период;  прогнозируемый показатель; параметр сглаживания; фактическое значение исследуемого показателя за период, предшествующий прогнозному;  экспоненциально взвешенная средняя для периода, предшествующего прогнозному.При прогнозировании данным методом возникает два затруднения: 1) выбор значения параметра сглаживания  ;2) определение начального значения Uо. Точного метода для выбора оптимальной величины параметра сглаживания α нет. В отдельных случаях предлагается определять величину α, исходя из длины интервала сглаживания. При этом α вычисляется по формуле: α = 2 / (n+1) В нашем случае: α = 2 / (10+1) = 0,182 0,2. Задача выбора Uо (экспоненциально взвешенного среднего начального) решается следующими путями: 1) если есть данные о развитии явления в прошлом, то можно воспользоваться средней арифметической, и Uо равен этой средней арифметической; 2) если таких сведений нет, то в качестве Uо используют исходное первое значение базы прогноза Y1. Определим начальное значение Uo двумя способами: І способ – как средняя арифметическая: Uo = (2,99 + 2,66 + …+ 1,42)/10 = 2,21. II способ - первое значение базы прогноза: Uo = 2,99. Далее рассчитываем экспоненциально взвешенную среднюю для каждого периода, используя приведенную выше формулу. Uфев = 2,99 х 0,2 +(1-0,2) х 2,21 = 2,37 (І способ) Uмарт = 2,66 х 0,2+(1-0,2) х 2,37 = 2,43 (І способ) и т.д. Uфев = 2,99 х 0,2 +(1-0,2) х 2,99 = 2,99 (II способ) Uмарт = 2,66 х 0,2+(1-0,2) х 2,99 = 2,92 (II способ) и т.д. По этой же формуле вычисляем прогнозные значения: Uноябрь= 1,42 x 0,2+(1-0,2) x 2,08 = 1,95 (І способ) Uноябрь= 1,42 x 0,2+(1-0,2) x 2,18 = 2,03 (ІІ способ). Сущность метода наименьших квадратов состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии. Рабочая формула метода наименьших квадратов: уt+1 = аХ + b, гдеt + 1 – прогнозный период; yt+1 – прогнозируемый показатель; a и b- коэффициенты; Х - условное обозначение времени. Расчет коэффициентов a и bосуществляется по следующим формулам: 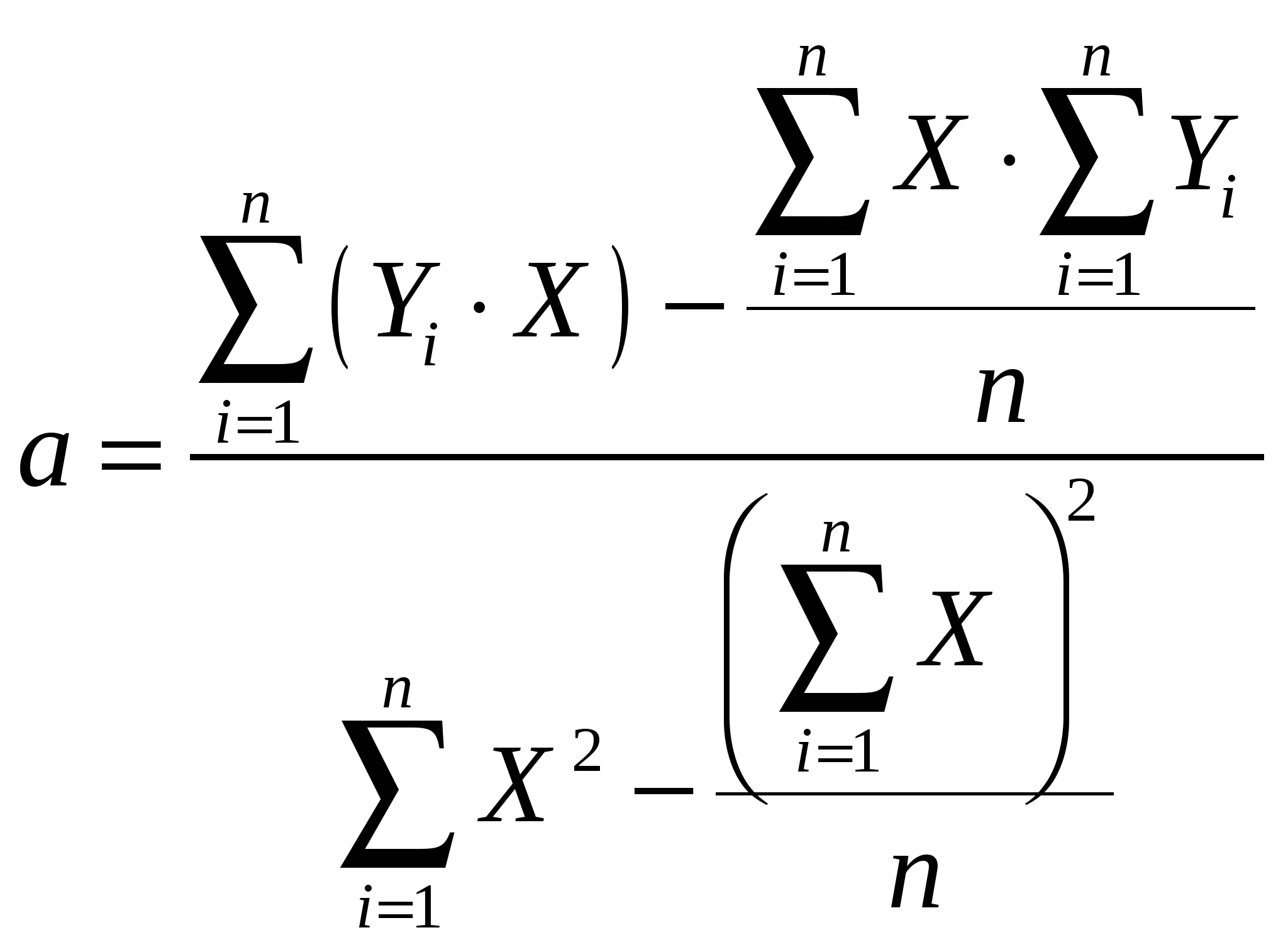 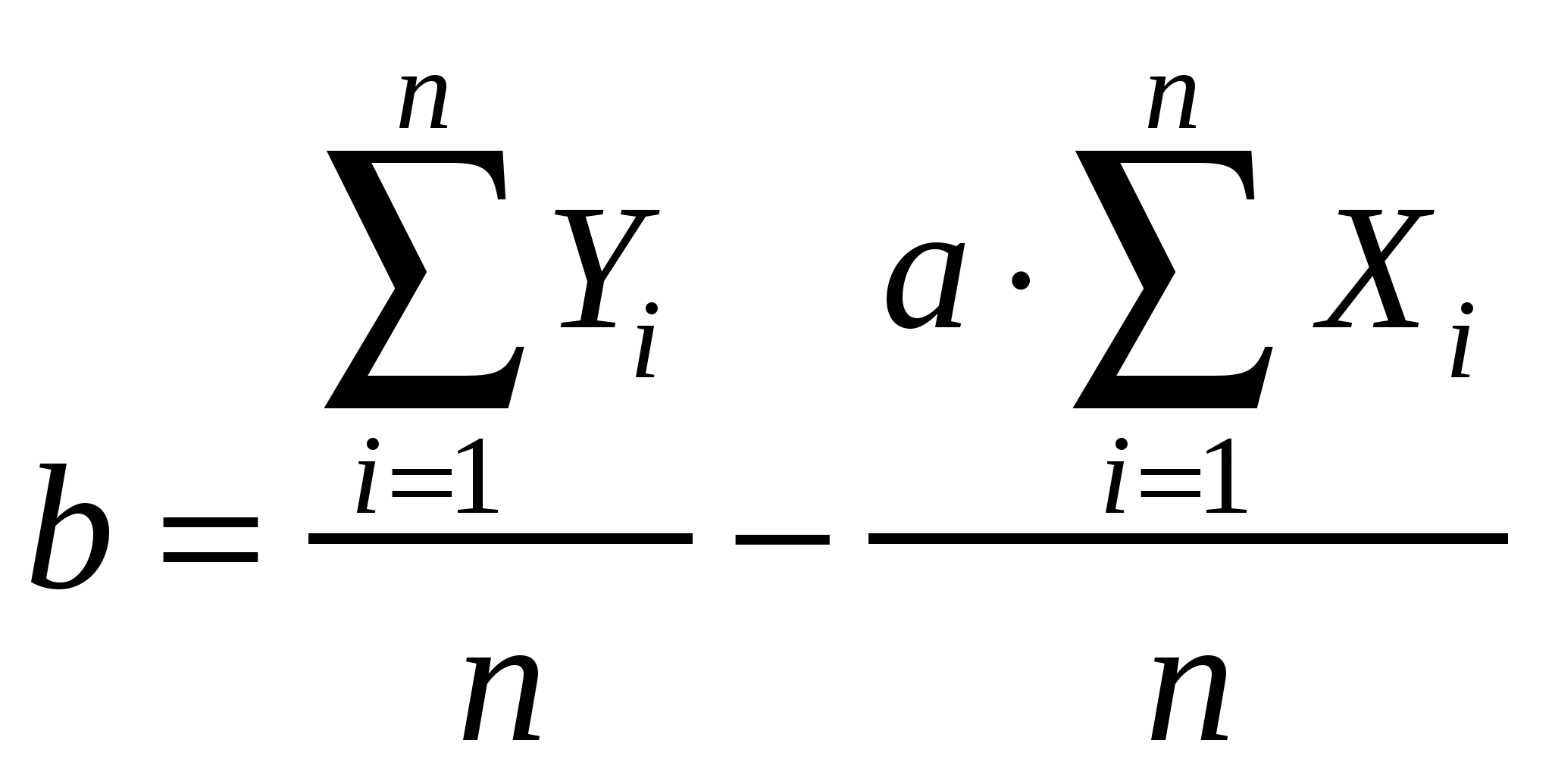 где  – фактические значения ряда динамики;n– число уровней временного ряда; В нашем случае:   Уравнение регрессии имеет вид: у = -0,172Х + 3,157, Построим прогноз уровня безработицы в регионе: - на ноябрь:  - на декабрь:  - на январь:  Определим по указанным выше формулам также расчетные значения для всего ряда, данные расчетов занесем в таблицу:
2. Построим график фактических и расчетных показателей: 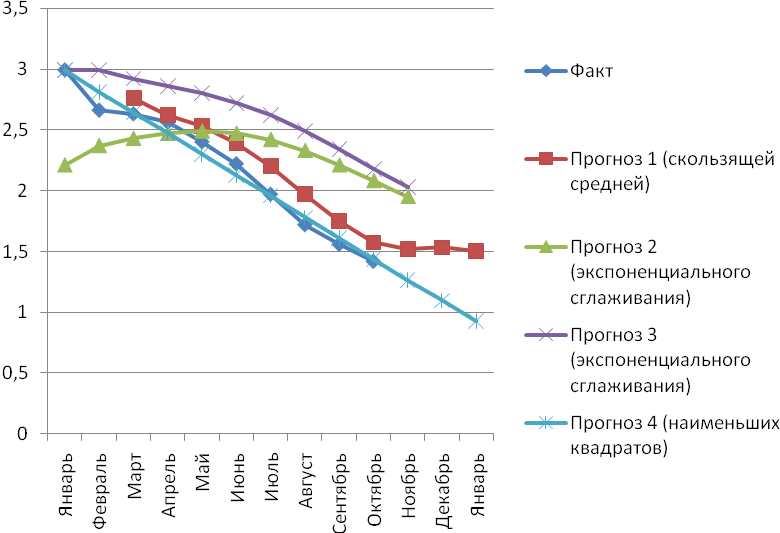 3. Рассчитаем ошибки полученных прогнозов. Существует несколько способов оценки точности прогнозов: 1) средняя абсолютная ошибка: Δ 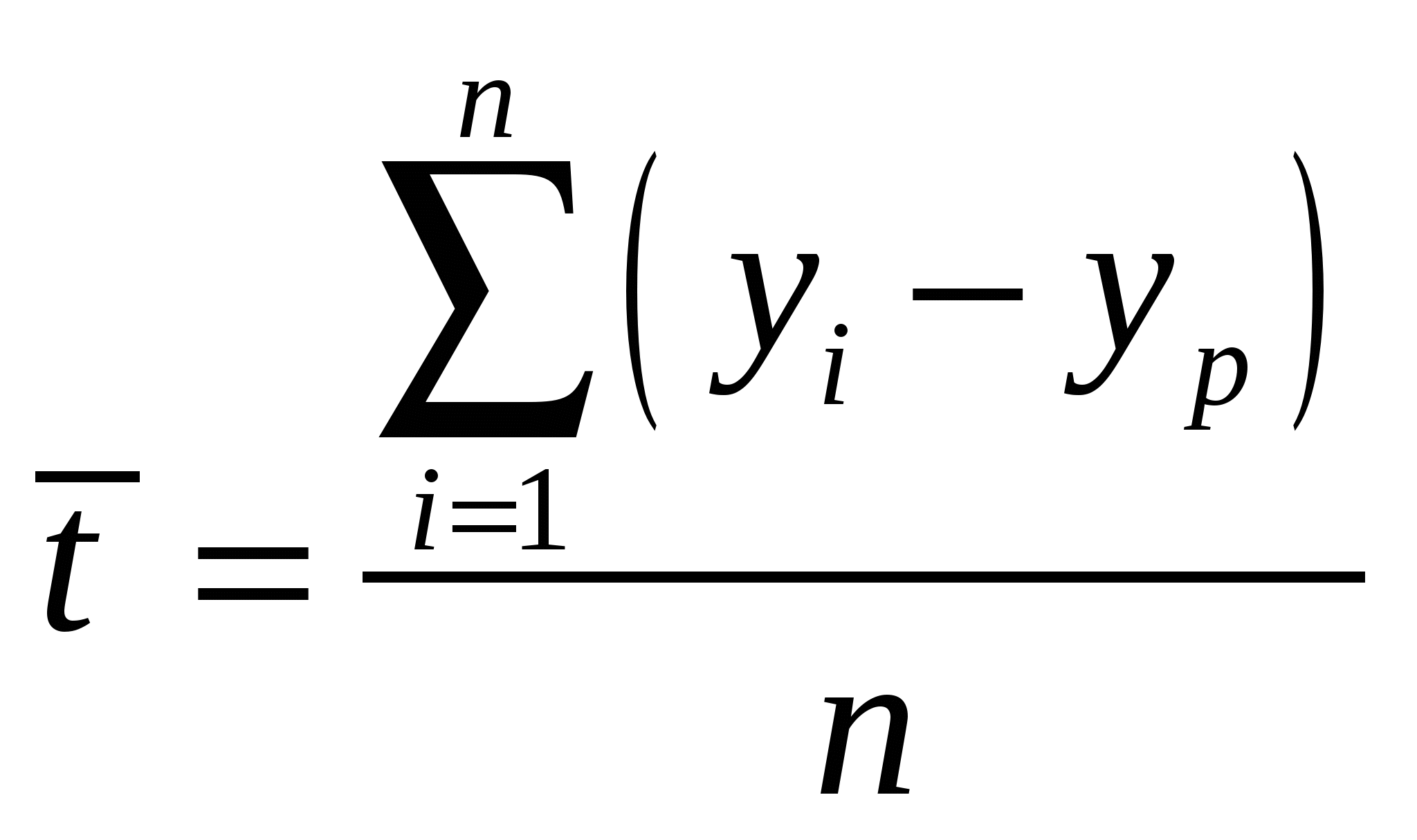 , где n – число уровней временного ряда; 2) средняя квадратическая ошибка: 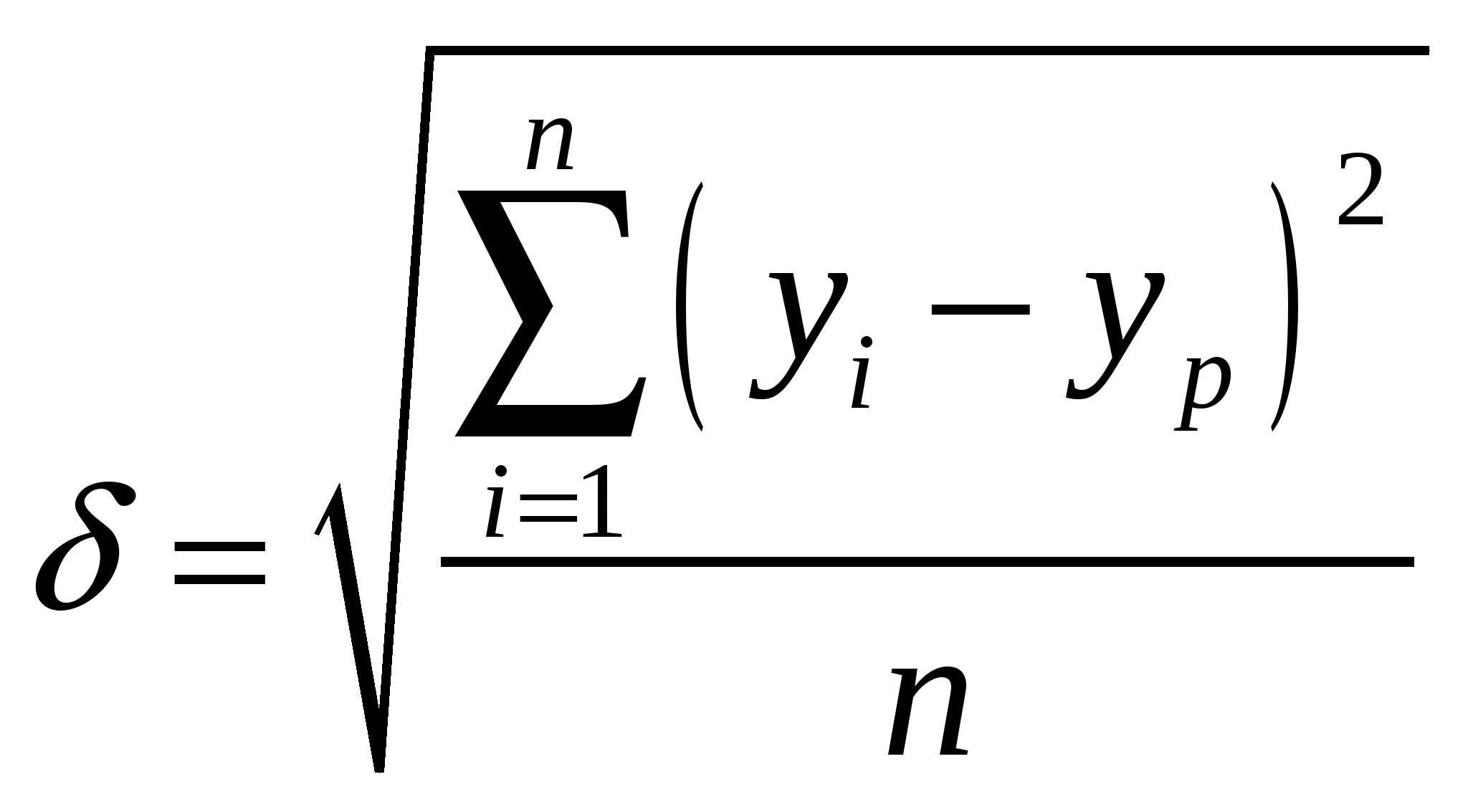 . 3) средняя относительная ошибка: 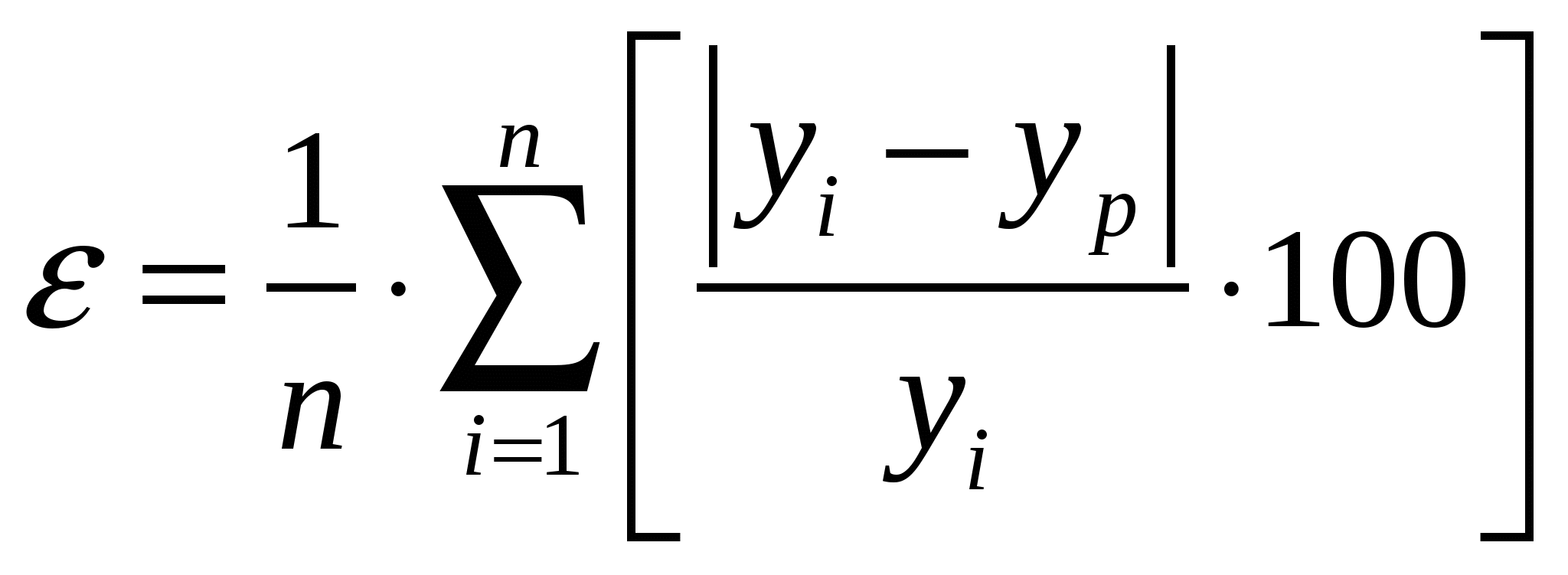 Чем ближе к нулю ошибка прогноза, тем выше его точность. Рассчитаем ошибки полученных прогнозов при использовании каждого метода, результаты расчетов занесем в таблицу:
Таким образом, более точным является прогноз по методу наименьших квадратов. Согласно данному прогнозу ожидается дальнейшее снижение уровня безработицы. В то же время, следует отметить, что недостатком метода наименьших квадратов является тот факт, что изучаемое экономическое явление мы пытаемся описать с помощью математического уравнения, поэтому прогноз будет точен для небольшого периода времени, и уравнение регрессии следует пересчитывать по мере поступления новой информации. |