Метрология к.р. Контрольная работа По дисциплине Метрология, стандартизация и сертификация на водном транспорте

• Название: Контрольная работа По дисциплине Метрология, стандартизация и сертификация на водном транспорте
• Дата: 03.10.2021
• Размер: 1 Mb.
• Имя файла: Метрология к.р.docx
• Тип: Контрольная работа; #240783
• страница: 2 из 3

Достоверностьизмерений определяется степенью доверия к результату измерения и характеризуется вероятностью того, что истинное значение измеряемой величины находится в указанных пределах. Данная вероятность называется доверительной.

Правильностьизмерений – это характеристика измерений, отражающая близость к нулю систематических погрешностей результатов измерений.

Сходимостьрезультата измерений – характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, выполняемых повторно одними и теми же методами и средствами измерений и в одних и тех же условиях. Сходимость измерений отражает влияние случайных погрешностей на результат измерения.

Воспроизводимостьрезультатов измерений – характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, полученных в разных местах, разными методами и средствами измерений, разными операторами, но приведенных к одним и тем же условиям.

Количественная близость измеренного и истинного значений измеряемой величины описывается погрешностью результата измерений.

Погрешность – это отклонение Х результата измерения Х_изм от истинного значения Х_нс измеряемой величины, определяемое по формуле

Х = X_изм – X_ис (1)

В зависимости от формы выражения различают абсолютную, относительную и приведенную погрешности измерения.

Абсолютная погрешность – это погрешность СИ, выраженная в единицах измеряемой физической величины. Она определяется как разность

∆= Хi − Х_д или ∆ = X − Х_д, где X_i – результат измерения.

Относительная погрешность – это погрешность СИ, выраженная отношением абсолютной погрешности СИ к результату измерений или действительному значению измеряемой физической величины. Она определяется как отношение δ = ±(∆/Х_д)·100 %.

Приведенная погрешность – это погрешность СИ, выраженная отношением абсолютной погрешности СИ к условно принятому значению величины, постоянному во всем диапазоне измерений Χ_N.

В качестве нормирующего значения можно использовать диапазон измерений прибора, верхний предел измерений и т.д. Она определяется как отношение γ = ±(∆/Χ_N)·100 %.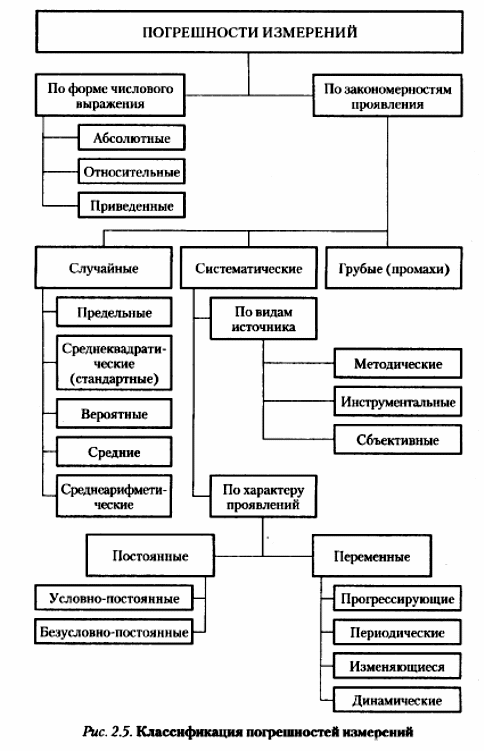


Рисунок 8 – Классификация погрешностей измерений
Принцип измерений, метод измерений.
Принцип измерений – совокупность физических принципов, на которых основаны измерения, например применение эффекта Джозефсона для измерения электрического напряжения или эффекта Доплера для измерения скорости.

Метод измерения – это прием или совокупность приемов сравнения измеряемой ФВ с ее единицей в соответствии с реализованным принципом измерения. Метод измерения должен по возможности иметь минимальную погрешность и способствовать исключению систематических погрешностей или переводу их в разряд случайных.

Методы измерения можно классифицировать по различным признакам. Известна классификация по основным измерительным операциям. Она тесно связана с элементарными СИ, реализующими эти операции. Данная классификация ориентирована на структурное описание средств измерений и поэтому важна для измерительной техники, а также метрологии информационно-измерительных систем.

Для метрологического анализа более важными являются традиционные классификации, основанные на следующих признаках. Первый из них – физический принцип, положенный в основу измерения. По нему все методы измерений делятся на электрические, магнитные, акустические, оптические, механические и т.д. В качестве второго признака классификации используется режим взаимодействия средства и объекта измерений. В этом случае все методы измерений подразделяются на статические и динамические. Третьим признаком может служить применяемый в СИ вид измерительных сигналов. В соответствии с ним методы делятся на аналоговые и цифровые.

Наиболее разработанной является классификация по совокупности приемов использования принципов и средств измерений. По этой классификации различают метод непосредственной оценкии методы сравнения(рис. 9). Представляется более правильным говорить о опосредованном и непосредственном сравнении с мерой. При этом непосредственным и опосредованным сравнение может быть как во времени, так и в отношении физической природы измеряемых величин.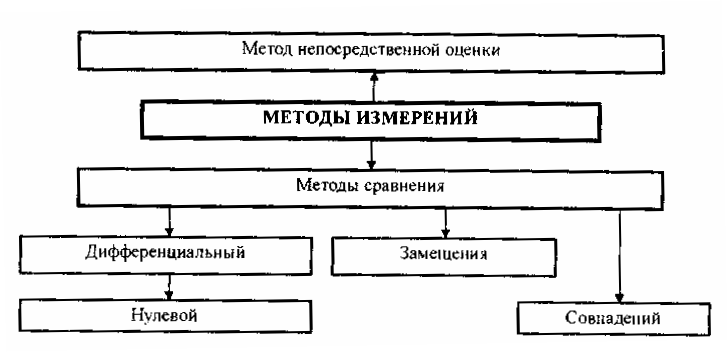


Рисунок 9 – Классификация методов измерения
Прямые измерения – основа более сложных измерений, поэтому целесообразно рассмотреть классификацию методов прямых измерений:

– Метод непосредственной оценки, при котором величину определяют непосредственно по отсчетному устройству измерительного прибора, например измерение давления пружинным манометром, массы – на весах.

– Метод сравнения с мерой, где измеряемую величину сравнивают с величиной, воспроизводимой мерой. Например, измерение массы на рычажных весах с уравновешиванием гирей; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС параллельного элемента.

– Метод противопоставления, при котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения. Например, определение массы на равноплечих весах с помещением измеряемой массы и уравновешивающих ее гирь на двух чашках весов.

– Дифференциальный метод, характеризуемый измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Метод позволяет получить результат высокой точности при использовании относительно грубых средств измерения.

– Нулевой метод, который аналогичен дифференциальному, но в нем разность между измеряемой величиной и мерой сводится к нулю. При этом нулевой метод имеет то преимущество, что мера может быть во много раз меньше измеряемой величины.

– Метод замещения, состоящий в том, что измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов.

– Метод совпадений, заключающийся в том, что разность между сравниваемыми величинами измеряют, используя совпадение отметок шкал или периодических сигналов. К примеру, при измерении длины штанген-циркулем наблюдают совпадение отметок на шкалах штангенциркуля и нониуса; при измерении частоты вращения стробоскопом наблюдают совпадение метки на вращающемся объекте с момента вспышек известной частоты.
Этапы измерительных процедур, их связь при постановке измерений, планировании измерений, проведении измерительного эксперимента.

Обработка экспериментальных данных.

Постановка измерительного эксперимента. При постановке измерительного эксперимента прежде всего требуется определить, какие по числу измерений (однократные или многократные) измерения следует осуществлять для определения значения измеряемой физической величины.

Общим здесь является следующий подход:

– если систематическая погрешность является определяющей, т.е. ее значение существенно больше значения случайной погрешности, то целесообразно использовать однократные измерения для получения значения измеряемой величины;

– если случайная погрешность является определяющей, то необходимо использовать многократные измерения.

Необходимо учитывать то, что систематическая погрешность вызывает смещение результатов измерений и является наиболее опасной тогда, когда о существовании ее не подозревают. Обнаружение систематической погрешности измерений является одной из наиболее сложных задач метрологии. В том или ином виде ее всегда приходится решать при подготовке к измерениям.

Для обработки экспериментальных данных прямых многократных измерений принято использовать методы математической статистики. При этом следует помнить, что применение этих методов позволяет получить корректные результаты только в том случае, когда из экспериментальных данных исключены систематические погрешности. Обработка экспериментальных данных прямых многократных измерений в общем случае предусматривает выявление закономерности поведения случайной погрешности (определения закона распределения) и статистические процедуры исключения грубых погрешностей.

Нормальный закон распределения является наиболее распространенным законом распределения случайных величин, в том числе и случайных погрешностей. Поэтому в практике обработки экспериментальных данных, когда число измерений мало (не превышает 5…25), пользуются вполне оправданным предположением, что закон распределения случайной погрешности является нормальным, а грубые погрешности не выявляются или определяются и отбрасываются интуитивно.

Методы математической статистики предполагают определение вместо характеристик нормального распределения их оценок. Так, вместо математического ожидания М[Х], т.е. значения величины, вокруг которого группируются результаты отдельных измерений при бесконечном числе измерений, определяют его оценку, которая представляет собой среднее арифметическое 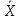при конечном числе измерений:

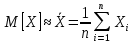(2)

где Xi – результат i-го измерения;

n – число измерений.

Вместо среднеквадратического отклонения σ, характеризующего рассеяние результатов отдельных измерений относительно математического ожидания, определяют оценку среднеквадратического отклонения результата измерений по формуле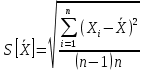
(3)
Также при обработке экспериментальных данных прямых многократных измерений принято вычислять интервальную оценку погрешности, которая определяется с использованием точечной погрешности S( 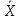) и доверительных интервалов.

Для обеспечения единства технических измерений задаются значением доверительной вероятности Р_д = 0,95 и определяют значение доверительного интервала. Коэффициент t обычно определяют по таблице, вместо того чтобы рассчитывать по сложной формуле, описывающей распределение Стьюдента.

Последовательность обработки экспериментальных данных прямых многократных измерений:

– результаты измерений являются исправленными, т.е. из них исключена известная систематическая погрешность;

– не исключённые систематические погрешности настолько малы, что ими можно пренебречь;

– результаты измерений являются равнорассеянными величинами (такие результаты получаются при выполнении измерений одним оператором с помощью одних и тех же СИ);

– из результатов измерений исключены грубые погрешности (промахи);

– число измерений не превосходит 15…25 (в этом случае признается и не проверяется нормальность распределения случайных погрешностей).

Алгоритм обработки экспериментальных данных прямых многократных измерений:

– Получение n результатов наблюдений.

– Вычисление среднего арифметического .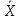

– Вычисление оценки среднеквадратического отклонения результата измерения S( ).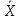

– Принятие значения доверительной вероятности Р_д (для технических измерений Р_д = 0,95).

– Определение коэффициента t в зависимости от Рд и n по таблице распределения Стьюдента.

– Определение доверительных границ ∆д случайной погрешности.

– Запись результата измерений с использованием правил округления в виде А = 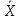± ∆_д с обязательным указанием (Рд = ; n = ).

Результаты однократных измерений также являются случайными величины, но из-за незнания закона распределения не могут быть подвергнуты статистической обработке. Поэтому результат прямого однократного измерения записывают в виде интервальной оценки:

Α = X ± ∆ (4)

где X – значение физической величины, найденное по шкале измерительного средства;

∆ – абсолютная погрешность для найденного значения X, определяемая по технической документации на СИ.

Для избежания получения промахов при однократных измерениях допускается проведение 2…3 замеров с нахождением среднего арифметического результата измерения, но без последующей статистической обработки.

Представление результатов измерений. Практикой обработки результатов измерительных экспериментов выработаны правила округления результатов, которые по соглашению признаются и применяются при выполнении любых, в том числе технических, измерений.

Погрешность результата измерения физической величины должна давать представление о том, какие цифры в его числовом значении являются сомнительными. Погрешность результатов технических измерений нецелесообразно выражать большим числом цифр. Достаточно ограничиться одной-двумя значащими цифрами. Причем две цифры используются только при записи погрешности ответственных, точных измерений.

Методика выполнения измерений. На обеспечение качества измерений направлено применение аттестованных методик выполнения измерений (МВИ). В 1997 г. начал действовать ГОСТ Р 8.600-2003 «Государственная система обеспечения единства измерений. Методики выполнения измерений. Общие требования» [10]. Статьи 9, 11 и 17 ФЗ РФ от 26 июня 2008 г. № 102-ФЗ «Об обеспечении единства измерений» также включают положения, относящиеся к МВИ.

МВИ – совокупность операций и правил, выполнение которых обеспечивает получение результатов с известной погрешностью. Под МВИ понимают технологический процесс измерений. Как правило, МВИ – это документированная измерительная процедура. В зависимости от сложности и области применения МВИ излагают либо в отдельном документе (стандарте, рекомендации), либо в разделе стандарта, части технического документа (ТУ, паспорта). Аттестация МВИ – процедура установления и подтверждения соответствия МВИ предъявляемым к ней метрологическим требованиям.

В документах, регламентирующих МВИ, в общем случае указывают:

назначение МВИ; условия измерений; требования к погрешности измерений; метод(ы) измерений; требования к СИ, вспомогательным устройствам, материалам, растворам и пр.; операции по подготовке к выполнению измерений; операции при выполнении измерений; операции обработки и вычисления результатов измерений; нормативы, периодичность и процедуру контроля погрешности результатов выполняемых измерений; требования к квалификации операторов; требования к безопасности и экологичности выполняемых работ.

При разработке МВИ одним из основных требований является обеспечение точности результата измерения, которая должна указываться в виде допускаемых значений абсолютной или относительной погрешности измерений. При этом ответственным этапом является анализ возможных источников и соответственно составляющих погрешности результата измерения: методических составляющих, инструментальных составляющих, погрешностей, вносимых оператором.
Взаимосвязь структурных элементов измерительного эксперимента в судовождении. Характерные признаки классификации измерений в судовождении и деление областей измерений
В период плавания на судне производятся различные измерения, наблю­дения и вычисления, конечными результатами которых является получение на путевой карте обсервованного или счислимого места судна на любой момент времени.Все сведения, прямо или косвенно влияющие на выработку координат места судна и элементов его движения составляют навигационную информацию.

Навигационная информация (НИ) – это совокупность сведений, прямо или косвенно определяющих местоположение судна на местности и его эле­менты  движения, а также результаты всех других навигационных измерений и вычислений.

К навигационной информации относятся следующие основные навигаци­онные элементы (НЭ):

– Координаты судна. Географические координаты используются для оп­ределения положения судна относительно экватора и гринвичского мериди­ана; полярные – относительно какого-либо подвижного или неподвижного объекта (ориентира, навигационной опасности, другого судна и т.п.), приня­того за начало координатной системы.

– Навигационные параметры (НП) – это измеряемые величины, зависящие от взаимного положения судна и ориентира (объекта, опорного пункта). НП являются функцией координат судна, поэтому по их значениям определяется место судна в географической или полярной системе координат.

– Элементы счисления, которые включают в себя: курсы, углы дрейфа, скорости судна и течения, время, пройденный путь и др.

– Поправки ТСН и методические поправки (поправки компаса и лага, склонение девиацию и т.д.).

– Измеренные моменты времени – это показания хронометров, часов и секундомеров в заданный момент времени.

– Параметры движения других судов (целей) и другие навигацион­ные величины.

Навигационная информация классифицируется по нескольким признакам:

– по виду измерений (прямая или непосредственно измеренная и косвенно измеренная);

– по своему составу (однородная и разнородная);

– по степени полноты (неполная, необходимая и избыточная);

– по отношению к результатам обработки (исходная и итоговая);

– по относительной точности (равноточная и неравноточная);

– по степени зависимости (независимая, статистически зависимая и функционально зависимая);

– по характеру измерения (дискретная и непрерывная).

Прямая (непосредственно измеренная) навигационная информация это такая информация, которая является прямым результатом физического процесса измерения. Сюда относятся пеленг, измеренный с помощью пеленгатора; курсовой угол, измеренный путем визирования ориентира; глубина, измеренная ручным лотом и др.

Косвенно измеренная информация является функцией непосредствен­но измеренных физических параметров. Функциональная зависимость НЭ от измеренных физических параметров реализуется с помощью преобразований, происходящих в самом измерительном приборе (Д_р в НРЛС вырабатывается преобразованием измеренного времени распространения ра­диоимпульса от судна до объекта и обратно), или же с помощью вычисли­тельных операций, выполняемых автоматически или вручную вне измери­тельного прибора (по измеренному вертикальному углу и высоте ориентира рассчитывается расстояние до него). Косвенно измеренные НЭ иногда называются вычисленными.

Однородная информация получается в результате измерений, основанных на одном и том же физическом принципе (высоты светил, измеренные СНО; радиопеленги, измеренные АРП и т.п.).

Разнородная информация получается в результате измерений, основанных на различных физических принципах (расстояние до ориентира, измеренное с помощью НРЛС и расстояние, вычисленное по измеренному секстаном вертикальному углу; компасный пеленг и радиопеленг; курс по гирокомпасу и курс по магнитному компасу и т.п.). Разнородными являются также НЭ, имеющие разное наименование (пеленг и высота, расстояние и глубина и т.п.).

 Неполная информация – если по ней невозможно определить искомые величины (один визуальный пеленг на ориентир при решении задачи определения места судна – это информация неполная, т.к. по одному параметру невозможно определить координаты судна).

Необходимая информация – это такая информация, которая обеспечи­вает расчет искомых величин (для определения места судна необходимо измерить минимум 2 НП).

Избыточная информация – информация, полученная сверх необходимой (3-й НП при определении места судна). Избыточная информация нужна для повышения точности решаемой задачи, т.е. для частичной компенсации случайных погрешностей и полного исключения промахов.

Итоговая информация определяет значения требующихся величин. Ито­говая информация, как правило, является результатом обработки некоторой исходной информации. Одна и та же информация в одном случае может быть исходной, в другом – итоговой (при решении задачи определения места коорди-наты судна являются итоговой информацией, а при определении элементов движения своего судна по обсервациям – исходной).

Равноточная информация – это такая информация, когда составляющие ее НЭ характеризуются одной и той же точностью. Равноточность НЭ обеспечивается при измерении их в статистически одинаковых условиях (приборы одинакового класса точности, операторами с одинаковой квалификацией и при неизменяющихся внешних факторах).

 Неравноточная информация – это такая информация, когда НЭ измерены с различной точностью, т.е. если числовые параметры, характеризующие точность НЭ, существенно различаются между собой.

Независимая информация – если каждый НЭ рассматриваемой их совокупности формируется под воздействием только своих частных случайных факторов.

Статистически зависимая информация – когда наряду с частными факторами в формировании НЭ участвует хотя бы один общий случайный фактор.

Функционально зависимая информация – если все рассматриваемые НЭ формируются только общими случайными факторами.

Дискретная информация – такая информация, которая измеряется че­рез какие-то интервалы времени (отсчеты, снимаемые со шкалы навигаци­онного прибора).

Непрерывная информация измеряется без перерывов в течение некоторого интервала времени (непрерывная запись курса курсографом и т.п.).