Статистика (1). Контрольная работа по дисциплине Статистика Вариант 5 Выполнила Дмитриева Е. А. Студент 2 курса специальности 036401. 65
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Решение: Затраты на рекламу - признак-фактор, прибыль - признак-результат. Средние значения и показатели вариации (среднеквадратическое отклонение и коэффициент вариации) для признака-фактора и признака-результата.: Проранжируем 1 ряд. Для этого сортируем его значения по возрастанию. Таблица для расчета показателей.
Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Простая средняя арифметическая Значение ряда 42 встречается всех больше (2 раз). Следовательно, мода равна x = 42 Медиана соответствует варианту, стоящему в середине ранжированного ряда. Находим середину ранжированного ряда: h = n/2 = 20/2 = 10. Ранжированный ряд включает четное число единиц, следовательно медиана определяется как средняя из двух центральных значений: (26 + 28)/2 = 27 Размах вариации R = Xmax - Xmin R = 44 - 15 = 29 Среднее линейное отклонение Каждое значение ряда отличается от другого в среднем на 8.24 Дисперсия Среднее квадратическое отклонение (средняя ошибка выборки). Каждое значение ряда отличается от среднего значения 28.4 в среднем на 9.36 Коэффициент вариации Поскольку v>30% ,но v<70%, то вариация умеренная. Проранжируем 2 ряд. Для этого сортируем его значения по возрастанию. Таблица для расчета показателей.
Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Простая средняя арифметическая Мода отсутствует (все значения ряда индивидуальные). Медиана. Находим середину ранжированного ряда: h = n/2 = 20/2 = 10. Ранжированный ряд включает четное число единиц, следовательно медиана определяется как средняя из двух центральных значений: (54 + 58)/2 = 56 Показатели вариации. Абсолютные показатели вариации R = Xmax - Xmin R = 97 - 29 = 68 Среднее линейное отклонение Каждое значение ряда отличается от другого в среднем на 14.85 Дисперсия Среднее квадратическое отклонение (средняя ошибка выборки). Каждое значение ряда отличается от среднего значения 55.95 в среднем на 17.92 Коэффициент вариации Поскольку v>30% ,но v<70%, то вариация умеренная. Поле корреляции. 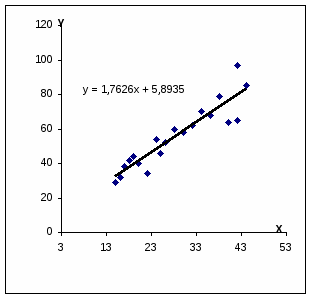 Данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение. Задача состоит в том, чтобы увидеть, есть связь между признаками или нет; прямая связь или обратная; линейная или нелинейная. Тогда ширина интервала составит: Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
Аналитическая группировка.
По аналитической группировке измеряют связь при помощи эмпирического корреляционного отношения. Оно основано на правиле разложения дисперсии: общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий. Находим средние значения каждой группы. млн. руб. млн. руб. млн. руб. млн. руб. Общее средние значение для всей совокупности: млн. руб. Дисперсия внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучением). Эта дисперсия называется остаточной: Расчет для группы: 15 - 22.25 (1,2,3,4,5,6,7)
Определим групповую (частную) дисперсию для 1-ой группы: Расчет для группы: 22.25 - 29.5 (8,9,10,11)
Определим групповую (частную) дисперсию для 2-ой группы: Расчет для группы: 29.5 - 36.75 (12,13,14,15)
Определим групповую (частную) дисперсию для 3-ой группы: Расчет для группы: 36.75 - 44 (16,17,18,19,20)
Определим групповую (частную) дисперсию для 4-ой группы: Внутригрупповые дисперсии объединяются в средней величине внутригрупповых дисперсий: Средняя из частных дисперсий: млн. руб. Межгрупповая дисперсия относится на счет изучаемого фактора, она называется факторной млн. руб. Определяем общую дисперсию по всей совокупности, используя правило сложения дисперсий: σ2 = 57.45 + 263.6 = 321.05 млн. руб. Проверим этот вывод путем расчета общей дисперсии обычным способом:
млн. руб. Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Это отношение факторной дисперсии к общей дисперсии: Определяем эмпирическое корреляционное отношение: Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < η < 0.3: слабая; 0.3 < η < 0.5: умеренная; 0.5 < η < 0.7: заметная; 0.7 < η < 0.9: высокая; 0.9 < η < 1: весьма высокая; В нашем примере связь между признаком Y фактором X весьма высокая На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер. Линейное уравнение регрессии имеет вид y = bx + a Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти. Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Система нормальных уравнений. a•n + b∑x = ∑y a∑x + b∑x2 = ∑y•x Для наших данных система уравнений имеет вид 20a + 568 b = 1119 568 a + 17884 b = 34869 Домножим уравнение (1) системы на (-28.4), получим систему, которую решим методом алгебраического сложения. -568a -16131.2 b = -31779.6 568 a + 17884 b = 34869 Получаем: 1752.8 b = 3089.4 Откуда b = 1.7626 Теперь найдем коэффициент «a» из уравнения (1): 20a + 568 b = 1119 20a + 568 • 1.7626 = 1119 20a = 117.87 a = 5.8935 Получаем эмпирические коэффициенты регрессии: b = 1.7626, a = 5.8935 Уравнение регрессии (эмпирическое уравнение регрессии): y = 1.7626 x + 5.8935 Для расчета параметров регрессии построим расчетную таблицу
Параметры уравнения регрессии. Выборочные средние. Выборочные дисперсии: Среднеквадратическое отклонение Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно: Коэффициент корреляции Ковариация. Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле: Линейный коэффициент корреляции принимает значения от –1 до +1. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < rxy < 0.3: слабая; 0.3 < rxy < 0.5: умеренная; 0.5 < rxy < 0.7: заметная; 0.7 < rxy < 0.9: высокая; 0.9 < rxy < 1: весьма высокая; В нашем примере связь между признаком Y фактором X весьма высокая и прямая. Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: Уравнение регрессии (оценка уравнения регрессии). Линейное уравнение регрессии имеет вид y = 1.76 x + 5.89 Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент регрессии b = 1.76 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 1.76. Коэффициент a = 5.89 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями. Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо. Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения. Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая. Коэффициент детерминации. R2= 0.9212 = 0.848 т.е. в 84.8 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 15.2 % изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации). Для оценки качества параметров регрессии построим расчетную таблицу
Оценка параметров уравнения регрессии. Анализ точности определения оценок коэффициентов регрессии. Несмещенной оценкой дисперсии возмущений является величина: S2 = 54.207 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии). S = 7.36 - стандартная ошибка оценки (стандартная ошибка регрессии). Проверка гипотез относительно коэффициентов линейного уравнения регрессии. 2) F-статистика. Критерий Фишера. Табличное значение критерия со степенями свободы k1=1 и k2=18, Fтабл = 4.41 Поскольку фактическое значение F > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). |
