Статистика (1). Контрольная работа по дисциплине Статистика Вариант 5 Выполнила Дмитриева Е. А. Студент 2 курса специальности 036401. 65
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ» Факультет торгового и таможенного дела Кафедра таможенного дела Контрольная работа по дисциплине «Статистика» Вариант №5 Выполнила Дмитриева Е.А. Студент 2 курса специальности 036401.65 срок обучения 5 лет № зачет. книжки 333411 Подпись_____________ Преподаватель______________________________________ Должность_________________________________________ (уч. степень, учебное звание) Оценка______________ Дата:____________________ Подпись_____________ Санкт-Петербург 2015 Задание 1. Абсолютные и относительные статистические показатели Имеются данные о реализации продукции филиалами предприятиями за отчетный год (млн. руб.):
Рассчитайте и запишите в таблицу недостающие данные. Определите: 1) относительные величины планового задания, выполнения плана и динамики реализации продукции для каждого филиала; 2) средние по предприятию уровни относительных показателей динамики, планового задания, выполнения плана. Покажите взаимосвязь относительных показателей планового задания, выполнения плана и динамики. Рассчитайте показатели структуры реализации (удельный вес выпуска продукции каждого филиала в общем объеме реализованной продукции) по плану и фактически (в прошлом и отчетном году). Расчеты относительных показателей выполните в процентах с точностью до 0,1. Результаты расчетов представьте в таблице. Решение: 1. Относительная величина планового задания = Упл / Уо * 100 17,9/15,6 * 100 = 114,7% 11,0/10,1 * 100 = 108,9% 34,5/37,9 * 100 = 91,03% 30,1 / 34,0 * 100 = 88,53% Относительная величина выполнения плана = У1/Упл * 100 24,9 / 17,9 * 100 = 139,1% 11,0/11,0 * 100 = 100,0% 30,1/34,5 * 100 = 87,3% 32,0 /30,1 * 100 = 106,3% Относительная величина динамики реализации = У1/Уо * 100 24,9 / 15,6 * 100 = 159,6% 11,0/10,1 * 100 = 108,9% 30,1/37,9 * 100 = 79,4% 32,0 /34,0 * 100 = 94,1% 2. Средние уровни рассчитываются по сумме показателей за все филиалы 93,5/97,6 * 100 = 95,8% 98,0 / 93,5 * 100 = 104,8% 98,0 / 97,6 * 100 = 100,4% 3. Взаимосвязь показателей ОВД = ОВПЗ*ОВВП 1,147 * 1,391 = 1,596 или 159,6% 1,089 * 1,000 = 1,089 или 108,9 % 0,9103 * 0,873 = 0,795 или 79,5% 0,8853 * 1,063 = 0,941 или 94,1% 4. Показатели структуры реализации Относительная величина структуры = Часть совокупности \ Вся совокупность * 100
Задание 2. Статистические показатели структурных сдвигов Используя показатели структуры реализации продукции предприятий в разрезе отдельных филиалов в 2011 и 2012 гг., рассчитанные в задаче 1, дайте характеристику изменения удельного веса каждого филиала в общем объеме реализации. С помощью обобщающих показателей структурных сдвигов определите, как в целом изменилась структура реализации за год. Расчеты выполните в табличной форме. Напишите, в чем состоит смысл рассчитанных показателей. Решение:
По результатам расчетов можно сделать вывод, фактически увеличился удельный вес первого филиала на 4% (21,4 по плану и 25,4 % фактически) и четвертого филиала 8,6% (24,1 по плану и 32,7% фактически). Удельный вес второго и третьего филиала фактически уменьшился до 11,2 и 30,7 %% соответственно. Интегральный коэффициент структурных сдвигов К. Гатева Линейный коэффициент структурных сдвигов: Квадратический коэффициент абсолютных структурных сдвигов: Линейный и квадратический коэффициенты абсолютных структурных сдвигов показывают, на сколько процентных пунктов в среднем отклоняются друг от друга сравниваемые удельные веса. Задание 3. Средние величины Имеются данные, характеризующие выбросы загрязняющих веществ в 2012 году по районам города:
Рассчитайте показатели в среднем по городу. Укажите, какие виды и формы средних вы использовали. Решение: Для расчета показателей используем среднюю арифметическую взвешенную 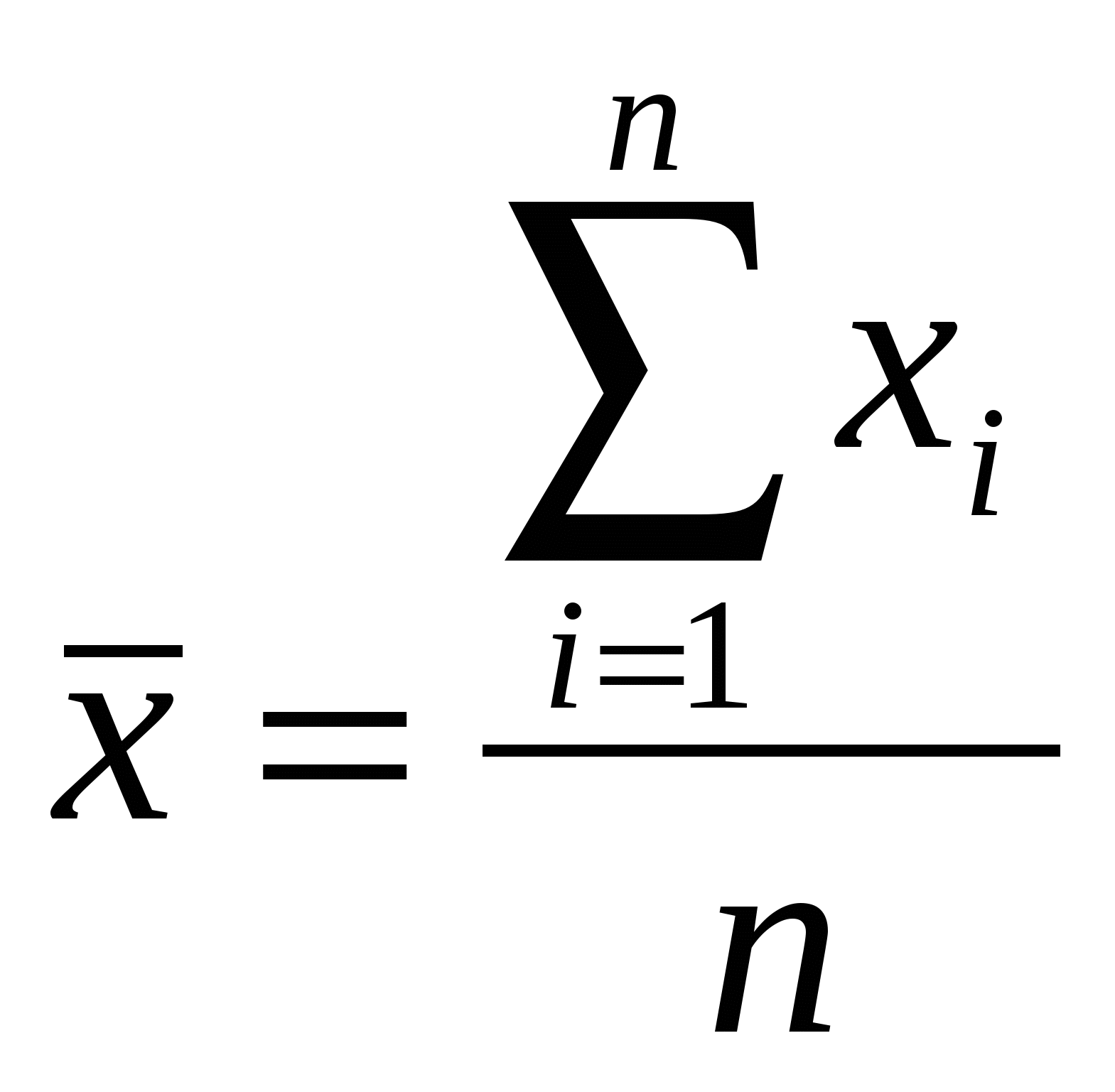 Средний размер выбросов = (3,3+9+1,2+4,2) / 4 = 4,425 тыс. тонн Средний размер выбросов на 1 человека = (7,2+28,2+3,7+9,6)/4 = 12,175 кг. Средний темп роста рассчитывается по формуле среднего темпа роста Средняя доля выбросов без очистки = (3,3 * 0,9+9*0,82+1,2*0,95+4,2*0,96)/17,7 = 0,877 или 87,7% Задание 4. Анализ вариации На основе соответствующих вашему варианту данных определите: 1. Характеристики центра распределения: − среднее значение признака; − модальное значение признака; − медианное значение признака. 2. Показатели размера и интенсивности вариации: − среднее линейное отклонение; − дисперсию; − среднее квадратическое отклонение; − коэффициент вариации. 3. Показатели формы распределения: коэффициенты асимметрии и эксцесса. Постройте гистограмму распределения. Раскройте содержание всех рассчитанных показателей и их представление на графике. В лаборатории комбикормового завода произведена контрольная проверка партии пшеницы, поступившей для производства комбикормов, на содержание протеина. В результате получены следующие данные:
Решение: Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Средняя взвешенная % Максимальное значение повторений при x = 10 (f = 19). Следовательно, мода равна 10 Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 26. Это значение xi = 10. Таким образом, медиана равна 10 Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = Xmax - Xmin R = 12 - 6 = 6 % Среднее линейное отклонение % Каждое значение ряда отличается от другого в среднем на 1.16 % Дисперсия % Среднее квадратическое отклонение (средняя ошибка выборки). % Каждое значение ряда отличается от среднего значения 9.3 в среднем на 1.42 % К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение. Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс. Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять. Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней. Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Чаще всего эксцесс оценивается с помощью показателя: Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) - отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3. M4 = 555.29/50 = 11.11 Число 3 вычитается из отношения μ4/ σ4 потому, что для нормального закона распределения μ4/ σ4 = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные - отрицательным эксцессом. Ex < 0 - плосковершинное распределение Чтобы оценить существенность эксцесса рассчитывают статистику Ex/sEx где sEx - средняя квадратическая ошибка коэффициента эксцесса. Если отношение Ex/sEx > 3, то отклонение от нормального распределения считается существенным. Поскольку sEx < 3, то отклонение от нормального распределения считается не существенным. 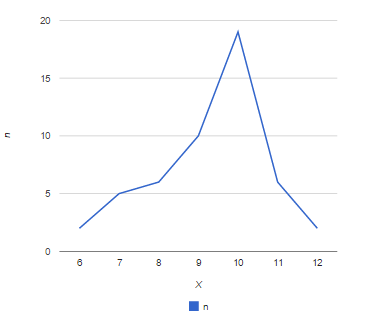 Задание 5. Выборочное наблюдение Проводится выборочное обследование населения с целью выявления процента удовлетворенных качеством предоставляемых медицинских услуг в поликлинических учреждениях города в рамках обязательного медицинского страхования. Численность населения в городе 315 тыс. человек. Сколько респондентов необходимо включить в выборку, если аналогичный опрос, проведенный в прошлом году, показал, что 25% опрошенных не устраивает качество представляемых медицинских услуг. Доверительная вероятность, с которой гарантируются оценки генеральной совокупности, должна составлять 0,95. Допустимая погрешность – не более 2%. Решение: Определим среднюю ошибку выборки для бесповторного отбора по формуле: Доверительной вероятности 0,954 соответствует доверительный коэффициент t=2,00 из таблицы значений интегральной функции Лапласа. Тогда предельная ошибка выборки для данной доверительной вероятности вычислим по формуле: Соответственно, с доверительной вероятностью 0,954 можно утверждать, что необходимо включить в выбору число человек в пределах от 7387 до 83,63 тыс. чел. Задание 6. Статистическое изучение связей На основе соответствующих вашему варианту данных: 1. Сформулировать задачу изучения взаимосвязи признаков, обосновать выбор признака-фактора и признака-результата. 2. Рассчитать средние значения и показатели вариации (среднеквадратическое отклонение и коэффициент вариации) для признака-фактора и признака-результата. 3. Построить поле корреляции. 4. Провести аналитическую группировку по признаку фактору, выделив 3-4 группы. Для каждой группы рассчитать среднее значение признака-результата. 5. Нанести на поле корреляции эмпирическую линию регрессии, построенную по групповым средним значениям признака-фактора и признака-результата. 6. Сформулировать гипотезу о наличии связи, её форме, направлении и тесноте. 7. Рассчитать показатели силы связи для каждой группы. Сделать выводы об изменении интенсивности влияния фактора на результат. В случае линейной (или близкой к линейной) связи рассчитать средний показатель силы связи для совокупности в целом. 8. Рассчитать внутригрупповые дисперсии, среднюю из внутригрупповых дисперсий, межгрупповую дисперсию, общую дисперсию. Проверить правило сложения дисперсий. 9. Рассчитать показатели тесноты связи: эмпирическое корреляционное отношение и коэффициент детерминации. Сделать выводы о роли изучаемого фактора в общем комплексе условий и причин, влияющих на результат. 10. Проанализировать зависимость фактора и результата методом парной регрессии и корреляции. Построить линейное уравнение регрессии. Дать интерпретацию параметров уравнения. 11. Оценить тесноту связи с помощью парного линейного коэффициента корреляции и коэффициента детерминации. Интерпретировать их значения. 12. Проверить статистическую значимость уравнения с помощью F-критерия. 13. Сравнить показатели силы и тесноты связи, рассчитанные по результатам аналитической группировки и методом регрессии и корреляции. Сделать вывод о линейном или нелинейном характере связи. По организациям одного вида деятельности изучается связь между затратами на рекламу и суммой полученной прибыли.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
