Статистика (1). Контрольная работа по дисциплине Статистика Вариант 5 Выполнила Дмитриева Е. А. Студент 2 курса специальности 036401. 65
 Скачать 0.52 Mb.
|
|
Задание 7. Статистическое изучение динамики На основе данных, соответствующих вашему варианту: 1. Постройте график, отражающий динамику изучаемого процесса. Тип графика подберите самостоятельно. 2. Определите цепные и базисные аналитические показатели динамики. Результаты расчетов оформите в виде таблицы. 3. Покажите взаимосвязь цепных и базисных абсолютных приростов и коэффициентов роста. 4. Рассчитайте средние показатели динамики: средний абсолютный прирост, средний коэффициент роста, средний темп прироста. 5. Произведите аналитическое выравнивание уровней ряда, используя уравнение линейного тренда. 6. Нанесите на график выровненные уровни динамического ряда. 7. Экстраполируйте ряд динамики на ближайшие два года на основе средних показателей динамики и на основе уравнения тренда. 8. Напишите краткие выводы. Имеются данные о производстве газобетона на комбинате железобетонных изделий:
Решение: Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными. Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким способом показатели динамики называются цепными. Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации. Абсолютный прирост цепной прирост: ∆yц = yi - yi-1 базисный прирост: ∆yб = yi - y1 Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения. Темп прироста цепной темп прироста: Tпрцi = ∆yi / yi-1 базисный темп прироста: Tпpб = ∆yбi / y1 Распространенным статистическим показателем динамики является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах. Темп роста цепной темп роста: Tpцi = yi / yi-1 базисный темп роста: Tpб = yбi / y1 Абсолютное значение 1% прироста цепной: 1%цi = yi-1 / 100% базисный: 1%б = yб / 100% 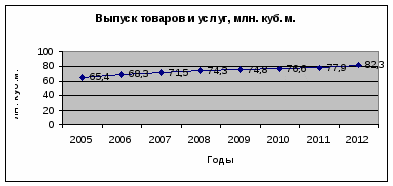 Цепные показатели ряда динамики.
Базисные показатели ряда динамики
Средний уровень ряда y динамики характеризует типическую величину абсолютных уровней. Средний уровень интервального ряда рассчитывается по формуле: млн. куб. м. Средний темп роста Средний темп прироста Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Средний абсолютный прирост млн. куб. м. Линейное уравнение тренда имеет вид y = a1t + a0 1. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК: a0n + a1∑t = ∑y a0∑t + a1∑t2 = ∑y • t
Для наших данных система уравнений имеет вид: 8a0 + 36a1 = 591.1 36a0 + 204a1 = 2751 Из первого уравнения выражаем а0 и подставим во второе уравнение Получаем a0 = 64.132, a1 = 2.168 Уравнение тренда: y = 2.168 t + 64.132 Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных. Коэффициент тренда b = 2.168 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на 2.168. 2. Анализ точности определения оценок параметров уравнения тренда. Стандартная ошибка уравнения. где m = 1 - количество влияющих факторов в модели тренда. 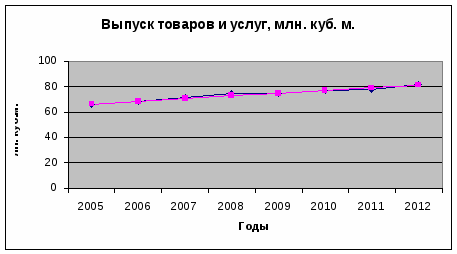 Интервальный прогноз. Определим среднеквадратическую ошибку прогнозируемого показателя. Uy = yn+L ± K где L - период упреждения; уn+L - точечный прогноз по модели на (n + L)-й момент времени; n - количество наблюдений во временном ряду; Sy - стандартная ошибка прогнозируемого показателя; Tтабл - табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2. По таблице Стьюдента находим Tтабл Tтабл (n-m-1;α/2) = (6;0.025) = 2.447 Точечный прогноз, t = 9: y (2013 год) = 2.17*9 + 64.13 = 83.64 млн. куб. м. 83.64 - 3.3 = 80.34 ; 83.64 + 3.3 = 86.94 млн. куб. м. Интервальный прогноз: t = 9: (80.34;86.94) Точечный прогноз, t = 10: y (2014 год) = 2.17*10 + 64.13 = 85.81 млн. куб. м. 85.81 - 3.54 = 82.27 ; 85.81 + 3.54 = 89.35 млн. куб. м. Интервальный прогноз: t = 10: (82.27;89.35) В 2012 по сравнению с 2011 выпуск товаров и услуг увеличился на 4.4 млн. куб. м. или на 5.65% Максимальный прирост наблюдается в 2012 (4.4 млн. куб. м.) Минимальный прирост зафиксирован в 2009 (0.5 млн. куб. м.) Темп наращения показывает, что тенденция ряда возрастающая, что свидетельствует об ускорении выпуска товаров и услуг В 2012 по сравнению с 2005 выпуск товаров и услуг увеличился на 16.9 млн. куб. м. или на 25.84% Среднее значение выпуск товаров и услуг с 2005 по 2012 составило 73.89 млн. куб. м. В среднем за весь период рост анализируемого показателя составил 1.03 В среднем с каждым периодом выпуск товаров и услуг увеличивался на 3%. С каждым периодом выпуск товаров и услуг в среднем увеличивался на 2.41 млн. куб. м. Задание 8. Агрегатные индексы Имеются данные о продаже продуктов в розничной торговле за два периода:
На основе соответствующих вашему варианту данных определить: 1) индивидуальные индексы физического объема реализации, цен и товарооборота; 2) общие индекс цен Пааше, Ласпейреса, Фишера; 3) общий индекс физического объема реализации;; 4) общий индекс товарооборота; 5) абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным всего, и в том числе, за счет изменения цен и физического объема реализации. Показать взаимосвязь полученных результатов. Решение: Определим индивидуальные индексы цен, физического объема и товарооборота Индивидуальный индекс физического объема  .Индивидуальный индекс цен  .Индивидуальный индекс товарооборота:  Тогда по первому виду продукта:  или 104% - т.е. объем продаж первого вида изменился на 4%. или 100,1% - т.е. цены на первый продукта изменились на 0,1%. или 105,2% - т.е. товарооборот первого товара увеличилась на 5,2%.По второму виду продукта  или 97,6%- т.е. объем продаж второго товара уменьшился на 2,4% или 101,4% - т.е. цены на второй вид товара увеличились на 1,4%. или 98,9% - товарооборот уменьшился на 1,1%.По третьему виду продукта:  или 100%- т.е. объем продаж третьего вида товара не изменился. или 107,7% т.е. цены на третий вид товара увеличились на 7,7%. или 107,7%, т.е.товарооборот увеличился на 7,7%Общий индекс товарооборота Общий индекс цен (метод Пааше) Общий индекс физического объема продукции (индекс Ласпейреса) Покажем взаимосвязь индексов I = Iq • Ip = 1.021 • 1.016 = 1.038 ∆Z = ∑q1 • p1 - ∑q0 • p0 ∆Z = 4832 - 4655 = 177 За счет всех факторов общий товарооборот увеличился на 3.8% или на 177 руб. ∆Zp = ∑q1 • p1 - ∑q1 • p0 ∆Zp = 4832 - 4754 = 78 За счет изменения цен сводный товарооборот возросли на 1.64% или на 78 руб. ∆Zq = ∑q1 • p0 - ∑q0 • p0 ∆Zq = 4754 - 4655 = 99 руб. За счет изменения объема выработанной продукции, товарооборот возросли на 2.13% или на 99 руб. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||