Контрольная работа по статистике. контрольная статистика. Контрольная работа по дисциплине Статистика
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
Контрольная работапо дисциплине: СтатистикаЗАДАНИЕ 10.1. По данным таблицы произвести группировку предприятий по размеру валовой продукции, выделив 4 группы. Установить зависимость прибыли предприятия от размера, численности и объема выпускаемой продукции. Сделать выводы. Таблица 1.1 Исходные данные
Для удобства произведем ранжирование ряда по валовой продукции. Таблица 1.2 Ранжированный ряд по валовой продукции, ден.ед.
Решение: Для группировки предприятий находим величину интервала, которая определяется по формуле: h = 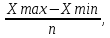 где xmax и xmin – максимальное и минимальное значение данного признака; n – число групп. min max x где n = 5. Таким образом, получается, что h = 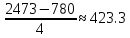 ден.ед. ден.ед.Сгруппировав предприятия по размеру валовой продукции, мы получили следующие таблицы: Таблица 1.3 Группировка предприятий
Таблица 1.4 Группировка предприятий
Таблица 1.5 Группировка предприятий
Таблица 1.6 Группировка предприятий
Для установления зависимости прибыли предприятия от размера, численности и объема выпускаемой продукции необходимо сделать группировку по прибыли. h = 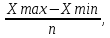 где h = 4. Для удобства произведем ранжирование ряда по прибыли. Таблица 1.7 Ранжированный ряд по прибыли, ден. ед.
Таким образом, получается, что h = 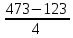 = 473-123/5=87.5 к первому интервалу принадлежит 3 предприятия, ко 2-му – 5, к 3-му – 5, к 4-му – 3. = 473-123/5=87.5 к первому интервалу принадлежит 3 предприятия, ко 2-му – 5, к 3-му – 5, к 4-му – 3.Как видно из приведенных выше таблиц, предприятия по валовой продукции распределены неравномерно. Наибольший процент к итогу по среднегодовой стоимости основных производственных фондов 61,03%, по численности персонала – 51,4% и по получению прибыли – 53%, принадлежит предприятиям с размером валовой продукции от 1203,3 до 1626,6 ден.ед. Таким образом, можно сказать, что при увеличении валовой продукции и численности рабочих, происходит прибыли. Соответственно между этими показателями существует прямая связь. ЗАДАНИЕ 10.2. Дальность перевозки каменного угля из одного бассейна характеризуется следующими данными: Таблица 1.1
Определите: Среднюю дальность перевозки; Моду и медиану; Коэффициент вариации; Постройте полигон и гистограмму распределения Таблица 1.2 Таблица для расчета показателей
Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Средняя взвешенная (выборочная средняя) Мода. Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота. Выбираем в качестве начала интервала 650, так как именно на этот интервал приходится наибольшее количество. Наиболее часто встречающееся значение ряда – 651.09 Медиана. Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше. Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных. В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 650 - 700, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот). Таким образом, 50% единиц совокупности будут меньше по величине 644.02. В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (xср=Me=Mo), а в умеренно асимметричных они соотносятся таким образом: 3(xср-Me) ≈ xср-Mo Среднее значение изучаемого признака по способу моментов. где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала. Находим А = 675 Шаг интервала h = 50 Средний квадрат отклонений по способу моментов.
Среднее квадратическое отклонение. Показатели вариации. Абсолютные показатели вариации. Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = xmax - xmin = 900 - 500 = 400 Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Каждое значение ряда отличается от другого в среднем на 67.33 Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). Среднее квадратическое отклонение. Каждое значение ряда отличается от среднего значения 648.36 в среднем на 83.322 Относительные показатели вариации. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение. Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс. Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять. Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины. Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней. Выводы: Каждое значение ряда отличается от среднего значения 648.36 в среднем на 83.322. Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки. Поскольку коэффициент вариации меньше 30%, то совокупность однородна. Полученным результатам можно доверять. Определение моды графическим способом 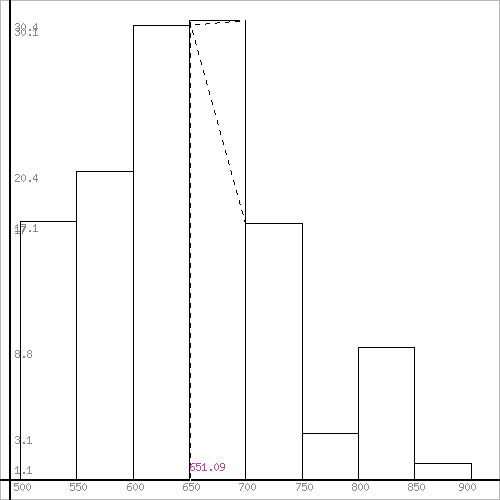 Рис. 1 Мода Определение медианы графическим способом 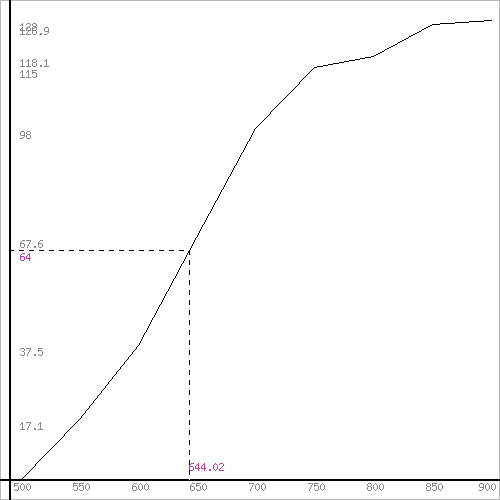 Рис. 2. Медиана 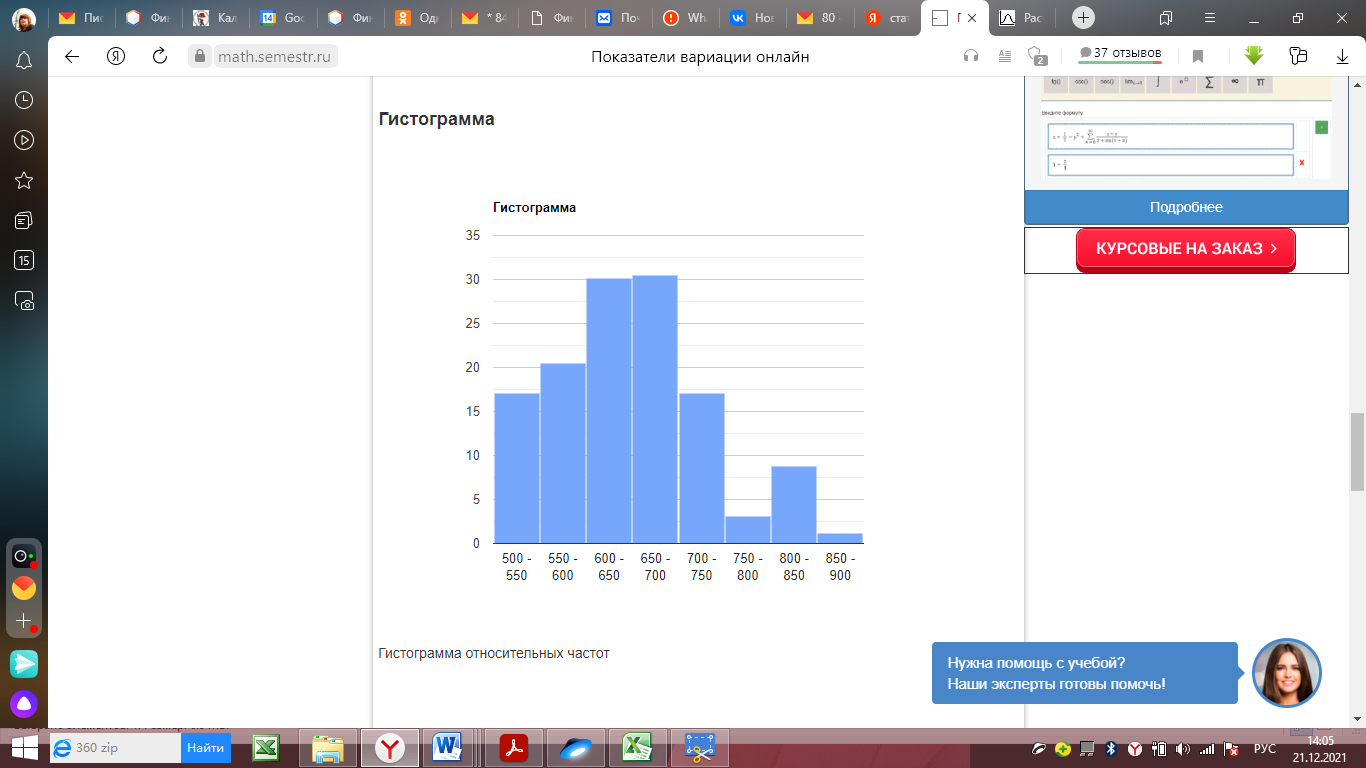 Рис. 3 Гистограмма 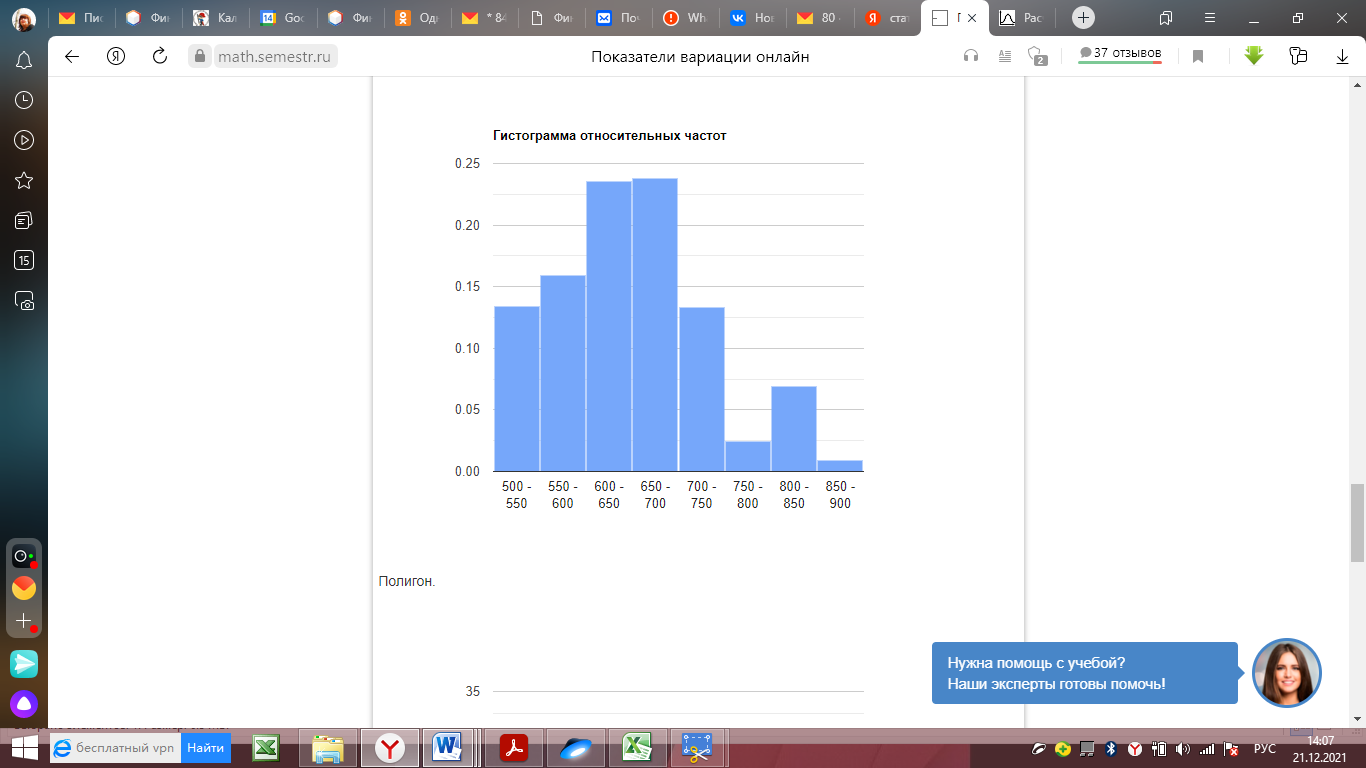 Рис. 4 Гистограмма относительных частот 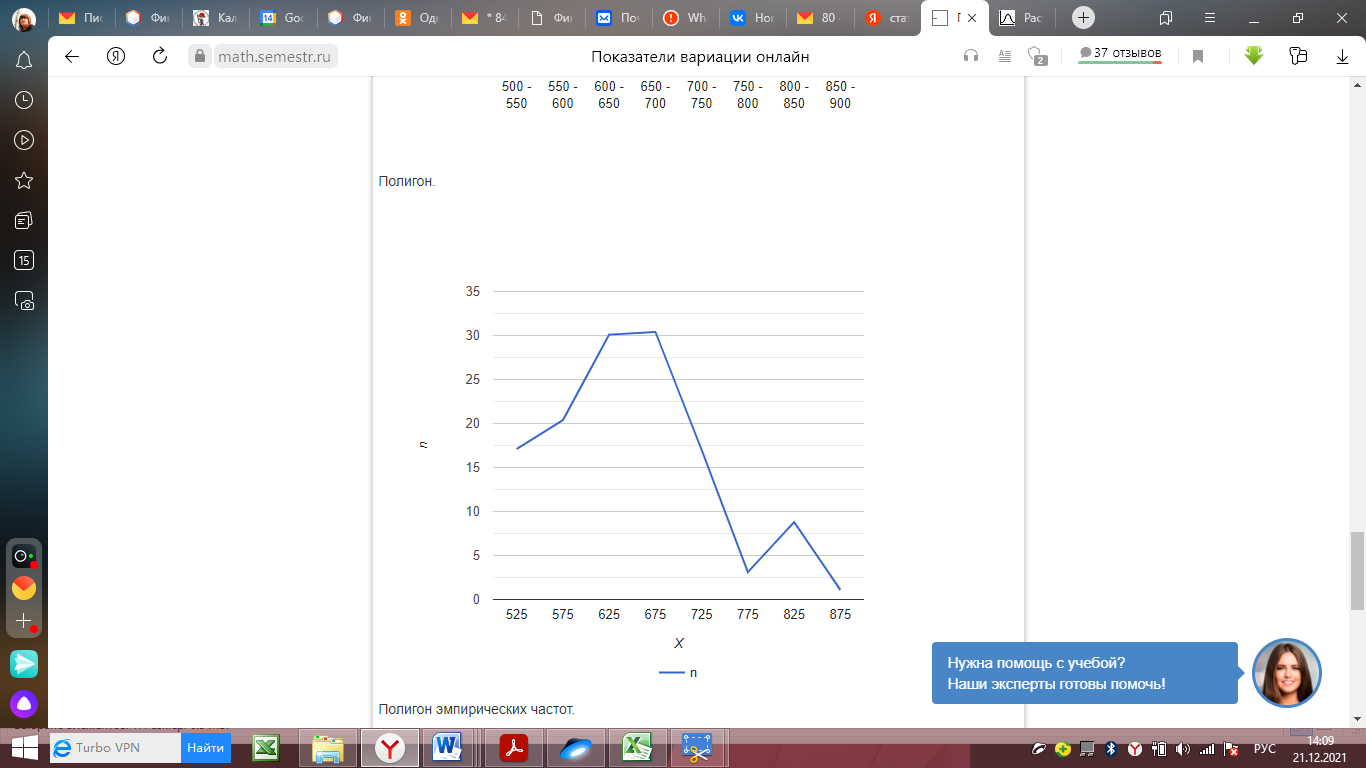 Рис. 5 Полигон 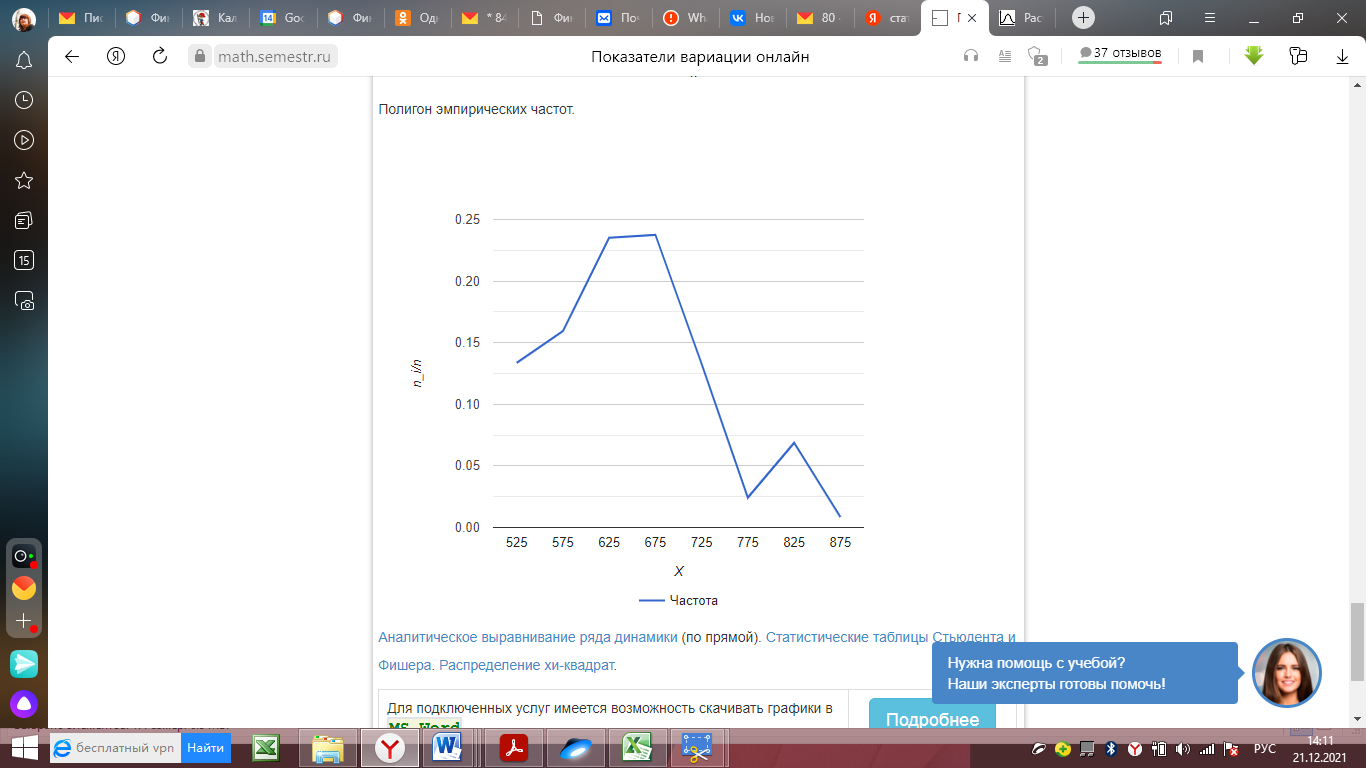 Рис. 6 Полигон эмпирических частот | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
