Контрольная работа по статистике. контрольная статистика. Контрольная работа по дисциплине Статистика

• Название: Контрольная работа по дисциплине Статистика
• Анкор: Контрольная работа по статистике
• Дата: 02.02.2022
• Размер: 0.78 Mb.
• Имя файла: контрольная статистика.docx
• Тип: Контрольная работа; #349456
• страница: 2 из 4

ЗАДАНИЕ 10.3. Произведено выборочное обследование длительности производ­ственного стажа рабочих. В выборку было взято 121 рабочих из общего количества в 1000 человек.

Результаты выборки следующие:

Продолжительность стажа, в годах	0-2	2-4	4-6	6-8	8-10
Число рабочих, чел.	27	40	32	10	12

Определите

1. 
   с вероятностью 0,997 возможные пределы колебания средней продолжительности производственного стажа всех рабочих.
   
2. 
   с вероятностью 0,95 возможные пределы удельного веса рабочих со стажем до 2 лет.
   

Решение:

Определим среднее выборочное значение: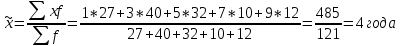


σ²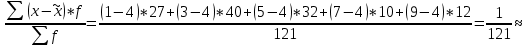⁼ 0.01

Определим выборочную дисперсию: 

Определим предельную ошибку выборки: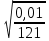

= 3 (1-0,1) = 0,02
Определим возможные пределы колебания средней продолжительности производственного стажа всех рабочих:



Подставив имеющиеся значения, получим:

4 – 0,02≤  ≤ 4 + 0,02 или 3,98 ≤ ≤ 4,02 года

Вывод: возможные пределы колебания средней продолжительности производственного стажа всех рабочих с вероятностью 0,997 составляют 3,98 - 4,02 года.

Задача 10.4

Коэффициент корреляции знаков.

Коэффициент корреляции знаков, или коэффициент Фехнера, основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Вычисляется он следующим образом:



где n_a - число совпадений знаков отклонений индивидуальных величин от средней;

n_b - число несовпадений.

Коэффициент Фехнера может принимать значения от –1 до +1. Kф = 1 свидетельствует о возможном наличии прямой связи, Kф = -1 свидетельствует о возможном наличии обратной связи.

Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:

Средние значения:

Xi	Yi	Знаки отклонений от средней X	Знаки отклонений от средней Y	Совпадение (а) или несовпадение (b) знаков
780	253	-	-	A
916	286	-	-	A
960	318	-	+	B
1230	196	-	-	A
1282	219	-	-	A
1300	305	-	+	B
1340	473	-	+	B
1344	318	-	+	B
1360	400	-	+	B
1367	276	-	-	A
1476	159	+	-	B
1564	304	+	+	A
1840	420	+	+	A
1913	351	+	+	A
1967	229	+	-	B
2473	123	+	-	B
23112	4630

Значение коэффициента свидетельствует о том, что можно предполагать отсутствие связи.

Оценка коэффициента корреляции знаков.

Значимость коэффициента Фехнера.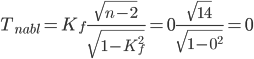



По таблице Стьюдента находим t_табл:

t_табл (n-m-1;a) = (14;0.05) = 2.145

Поскольку Tнабл < tтабл, то принимаем гипотезу о равенстве 0 коэффициента корреляции знаков. Другими словами, коэффициент Фехнера статистически - не значим.

Задача 5.

Производство продукции N характеризуется следующими данными:

Год	Объем производства, тыс. шт.	Год	Объем производства, тыс. шт.	Год	Объем производства, тыс. шт.
2006 г.	75	2010 г.	71	2014 г.	94
2007 г.	74	2011 г.	86	2015 г.	78
2008 г.	94	2012 г.	72	2016 г.	73
2009 г.	94	2013 г.	83	2017 г.	82

Экстраполируйте объем производства на 2018 год:

1) на основе среднего абсолютного прироста;

2) на основе среднего темпа роста;

3) на основе аналитического выравнивания уровней ряда.

Сравните полученные результаты