ТПР. Контрольная работа по дисциплине Теория принятия решений
 Скачать 69.6 Kb. Скачать 69.6 Kb.
|
|
Министерство образования Республики Беларусь БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Энергетический факультет Кафедра «Экономика и организация энергетики» Контрольная работа по дисциплине «Теория принятия решений » Выполнила: студентка гр.30607118 Евдоковец А.К Проверил : Лапченко Д.А. Минск 2022 Введение Существует большое количество видов и классификаций рисков в зависимости от специфики деятельности компании. Отдельно классифицируются инвестиционные риски, риски на рынке недвижимости, риски на рынке ценных бумаг и пр. В процессе своей деятельности предприниматели сталкиваются с совокупностью различных видов риска, которые отличаются между собой по месту и времени возникновения, совокупности внешних и внутренних факторов, влияющих на их уровень и, следовательно, по способу их анализа и методам описания. Как правило, все виды рисков взаимосвязаны и оказывают влияния на деятельность предпринимателя. При этом изменение одного вида риска может вызывать изменение большинства остальных. Классификация рисков означает систематизацию множества рисков на основании каких-то признаков и критериев, позволяющих объединить подмножества рисков в более общие понятия Раздел 1. Моделирование процессов принятия управленческих решений Моделирование есть "исследование каких-либо явлений, процессов или систем объектов путем построения и изучения их моделей, исследование моделей для определения или уточнения характера и рационализации способов построения вновь конструируемых систем и объектов" [1]. Моделирование предоставляет возможность изучения объекта не непосредственно, а через рассмотрение другого, подобного ему и более доступного объекта – его модели. Модель (от лат. modulus – образец, изображение, образ) – это создаваемое человеком подобие реального объекта. Наиболее широко моделирование используют в технике, автомобилестроении, авиации, космической отрасли, геодезии, архитектуре и др. Основные свойства моделей состоят в следующем: во-первых, модель должна быть подобна исследуемому объекту, а во-вторых, модель должна быть проще изучаемого объекта, чтобы оказалось возможным ее изучение. Основное назначение модели заключается в возможности проведения с моделью экспериментов, анализа и изучения, которые невозможны с самим исследуемым объектом. Моделирование как метод исследования систем управления применяется при разработке достаточно сложных управленческих решений и представляет собой построение моделей или системы моделей исследуемого объекта для его изучения. Исследование моделей объектов позволяет уточнить свойства и характеристики изучаемого явления. Использование моделей объектов позволяет проводить активные эксперименты, которые невозможны с самим исследуемым объектом. Проблемы применения моделирования изучаются во многих науках, но особенно они актуальны в сфере экономики. Необходимость моделирования обусловлена сложностью организационных ситуаций, невозможностью экспериментирования с реальными объектами и ориентацией управления на будущее (анализ последствий выбираемых альтернатив). При принятии решений в менеджменте естественен неформальный и качественный образ мышления, который вполне оправдывает себя в простых случаях, но в сложных ситуациях уже недостаточен. Справиться со сложностью можно, лишь переходя от "естественных" неформальных, качественных процессов мышления к формализованным, количественным или хотя бы дополняя первые вторыми. К тому же при осуществлении самого процесса построения модели не очень ясные, недостаточно четкие ситуации проясняются, и тем самым уровень осведомленности о системе повышается. Если невозможно построить удовлетворительную модель системы, то это свидетельствует, как правило, о недостаточном уровне знаний об объекте. Различают модели физические, аналоговые и математические. В экономике и управлении создать физический аналог (модель) объекта управления крайне сложно, а чаще всего просто невозможно; для оценки решений можно использовать не прямые аналоги – образцы исходного объекта, а описания, схемы, расчетные математические соотношения, которые аналитически, с помощью формул связывают между собой его характеристики. Подобный подход ничем не отличается от традиционного моделирования, однако в качестве модели (образца) в этом случае выступает не физический аналог исходного объекта, а система математических соотношений. Соотношения, устанавливающие взаимосвязь между характеристиками объекта управления и показателями эффективности (критериями), называют математическими моделями. В более широком понимании математическая модель – это приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Возможность применения и создания математических моделей для принятия управленческих решений во многом обусловлена тем, что большинство решений, как правило, можно связать с набором вполне определенных количественно измеримых величин, характеризующих как сам объект управления, так и внешнюю среду. Количественно измеримые величины и характеристики, с помощью которых ЛПР может осуществлять управление, называют управляемыми переменными или переменными решения. Факторы, влиять на которые или изменять которые ЛПР не в состоянии (параметры внешней среды, некоторые параметры самого объекта управления), называют неуправляемыми переменными или параметрами (ограничениями). Схема так называемого черного ящика иллюстрирует идею построения математической модели для объектов управления (рис. 1.1). С помощью аналитических соотношений (формул, уравнений, систем уравнений) модель должна связывать "входы" (характеристики объекта управления и параметры внешней среды) с "выходами" – показателями эффективности (критериями). 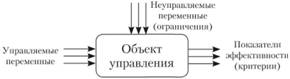 Рис. 1.1. Схема построения математической модели для объектов управления ("черный ящик") При построении математической модели управленческая ситуация упрощается и схематизируется. Из множества факторов в нее включают наиболее важные и весомые так, чтобы существующие закономерности можно было описать с помощью математического аппарата. Общих способов построения математических моделей не существует. В каждом конкретном случае модель строится исходя из целевой направленности управленческих решений с учетом требуемой точности решения, а также точности, с которой могут быть известны исходные данные. Располагая математической моделью объекта управления, можно решать различные задачи: оценивать те или иные решения, проводить исследования "что будет, если..." и др. Большой интерес представляют задачи, связанные с отысканием наилучшего из возможных решений, которые называют задачами оптимизации. Выбор критериев (показателей эффективности) и принципов оптимизации (максимизировать или минимизировать критерий) – прерогатива ЛПР. Определяющим фактором при этом всегда является цель. Выбор критерия позволяет найти ответ и на второй вопрос, а именно: определить и отобрать те характеристики объекта управления, с помощью которых (изменяя которые) ЛПР может управлять процессом. Такие характеристики, как было отмечено ранее, называют управляемыми переменными или переменными решения. Для оценки количественного влияния управляемых переменных на критерий необходимо либо иметь, либо создать математическую модель объекта управления [см. выражение (3.1)], т.е. получить аналитические соотношения (формулы). Если критерий оптимальности обозначить через Z, а переменные решения – через {x1, x2, ..., хп}, то взаимосвязь между критерием и управляемыми переменными можно символически представить как некую функцию Z = f(x1, x2, ..., хп), (3.1) которую в задачах оптимизации принято называть целевой функцией. Такие модели называют моделями принятия решения. Вопрос о том, в каких пределах можно варьировать (изменять) управляемые переменные для достижения наилучшего результата, во многом определяется тем, насколько ЛПР свободно или ограничено в выборе переменных {x1, x2, ..., хп}. В большинстве задач оптимизации, как правило, присутствуют ограничения, накладываемые на управляемые переменные. Если эти ограничения удается записать в аналитическом виде, то помимо целевой функции задача оптимизации будет содержать совокупность ограничений, которую также можно представить как систему неких математических соотношений. Вид ограничивающих соотношений (тип функциональной связи, их запись в виде уравнений либо неравенств) зависит от решаемой задачи и в каждом конкретном случае различен. Принципиальным является то, что любые ограничения снижают возможности выбора и, следовательно, число возможных решений. В связи с этим в задачах оптимизации широко используют понятие области допустимых решений, т.е. области, выделяемой из множества всех значений управляемых переменных, только внутри которой и допустим поиск оптимального решения {x1, x2, ..., хп}. Очевидно, что область допустимых решений полностью определяется системой ограничений. Таким образом, математически задача оптимизации в самом общем виде формулируется следующим образом: требуется найти такой набор значений для переменных решения {x1, x2, ..., хп}*, который обращает критерий оптимальности Z в max (min) при условии, что {x1, x2, ..., хп}* удовлетворяет заданной системе ограничений. Запись целевой функции в совокупности с условием оптимизации (максимизация или минимизация) и системой ограничений называют моделью оптимизации. Модель всегда тесно связана с проблемой, так как решение проблемы всегда начинается с моделирования проблемной ситуации объекта, а затем уже переходят к моделированию стратегических альтернатив и последствий принимаемого решения, куда, естественно, включаются такие элементы, как цель развития объекта управления, состояние внешней среды, функционирование объекта. Построение соответствующих математических моделей, используемых в управлении для принятия решений, предусматривает следующие этапы: постановка задачи принятия решения, создание модели, проверка модели, применение модели. Постановка задачи является основным этапом построения модели и представляет собой диагностику проблемной ситуации, т.е. идентификацию проблемы управляемого объекта. Создание модели – разработка формализованной схемы, которая включает в себя установление цели модели, выходной информации, получаемой из модели об объекте управления, помогающей ЛПР решать проблему, входной информации, необходимой для решения, и источников данной информации. Одним из основных этапов построения аналитической модели является разработка формализованной схемы, которая для задачи принятия решений имеет следующий вид: < S0,T,R | S, Z, Y, f, K >, где 50 – описание исходной проблемной ситуации; Т– время, располагаемое для принятия решения; R – ресурсы, учитываемые при принятии решения; 5 = {S1, S2, ..., Ss} – множество возможных ситуаций; Z= {Z1, Z2, ..., Zk} – множество целей, которые необходимо достичь в результате устранения проблемной ситуации S0; Y = {Y1, Y2, ..., Yn} – множество возможных решений; f = f (S, Y, Z) – функция предпочтения ЛПР, с помощью которой он оценивает ситуацию и решения по степени достижения множества целей; К – критерий выбора полученного решения. Для каждой конкретной ситуации Sj, решения Yi и цели Zi функция f (Sj, Yi, Zi) определяет полезность решения Yi в ситуации Sj для достижения цели Zi. В выражении (3.2) слева от вертикальной черты расположены известные элементы задачи, справа от вертикальной черты – элементы, которые необходимо определить. В ряде случаев располагаемое время и ресурсы для принятия решений также могут быть неизвестными, тогда их обозначения должны быть перенесены направо от вертикальной черты. Высказывание предпочтений на множестве ситуаций, решений и целей и формулировка критерия выбора позволяют определить одно или несколько оптимальных решений, обеспечивающих устранение проблемной ситуации. Значение таких моделей принятия решений заключается в возможности находить оптимальное решение через алгоритм и выбирать такие решения (возможные действия), которые гарантируют наилучшее достижение цели. Проверка модели предполагает проверку соответствия построенной модели реальной проблемной ситуации. Как правило, такую проверку на достоверность совершают, используя прошлые ситуации, т.е. используют информацию о состоянии объекта управления в прошлом, проблемах и последствиях уже принятых и реализованных управленческих решений. Применение модели возможно после проверки модели на ситуациях в прошлом, для этого необходимо собрать нужную информацию. В практической деятельности чаще всего используются подробно освещенные в литературе следующие виды моделей: статистические (вероятностные), имитационные, сетевые, линейного и математического программирования, теории очередей (массового обслуживания), запасов и др. Раздел 2. Обоснование решений на основе методов, моделей, алгоритмов и процедур экспертного и системного анализа. Задача 1. Фирма планирует реализацию одного из коммерческих проектов. Причем известны экспертные оценки, связанные с реализацией этих проектов (таблица 1). Выбрать рациональный вариант коммерческого проекта, если среднегодовая прибыль от реализации проекта должна быть не менее 4,5 млн. у.е. при минимальном риске. Задачу решить по следующей схеме: оценить эффективность проекта по критерию ожидаемой среднегодовой прибыли, определить допустимые проекты, исходя из заданного уровня среднегодовой прибыли, оценить риск допустимых проектов на основе коэффициента вариации ожидаемой среднегодовой прибыли, из множества допустимых проектов выбрать рациональный вариант коммерческого проекта, которому соответствует минимальный риск. Оценка ожидаемой прибыли Проект
Решение Степень риска коммерческого проекта возможно оценить с помощью коэффициента вариации, который характеризует относительный разброс случайной величины в виде ожидаемой прибыли от реализации проекта. Чем больше коэффициент вариации, тем больше неопределенность в отношении ожидаемой прибыли и, следовательно, тем больше степень риска коммерческого проекта. Причем принято выделять следующие уровни риска: Kvar < 10% - малая степень риска; Kvar = (10-25)% - средняя степень риска; Kvar > 25% - высокая степень риска. MO и SIGMA ожидаемой среднегодовой прибыли от реализации коммерческих проектов определяется на основе приближенных соотношений для Оценка степени риска коммерческого проекта
По критерию ожидаемой среднегодовой прибыли (МО) предпочтителен проект № 5 (самая большая прибыль); По уровню среднегодовой прибыли (SIGMA) наиболее благоприятен проект №2 (уровень равен 1,0). На основе коэффициента вариации выберем проект № 2 (самая малая степень риска). Из множества допустимых проектов выбрать самым рациональным является проект №2. Задача 2. Фирма планирует создание сервисного центра по обслуживанию и сопровождению своих изделий. Прибыль сервисного центра зависит от количества АРМ xj и потока заказов на обслуживание Si. Задачу решить по следующей схеме: осуществить выбор рациональной стратегии, используя перечисленные критерии: Лапласа; Байеса с вероятностями 0,15; 0,5; 0,35, Вальда; Сэвиджа; Гурвица (α=0,4); определить рациональное компромиссное решение; обосновать полученное решение с использованием рассчитанных критериев для принятия решения в условиях неопределенности. Исходные данные для расчета:
Решение Выбор рационального проекта (стратегии, альтернативы) осуществляется с использованием различных критериев для оптимизации решений в условиях неопределенности. Разработкой рекомендаций для выбора наилучшего варианта действий в условиях неопределенности занимается теория статистических решений. Эта математическая теория рассматривает игры с природой, в которых под природой понимаются объективные обстоятельства, внешняя среда. Считается, что природа сознательно не противодействует игроку. Условие задачи представлено в виде матрицы выигрышей (aji) игры с природой: Матрица игры
xj – стратегии сознательного игрока, Si – состояния природы, aji – выигрыш сознательного игрока при использовании им стратегии xj, если состоянием природы будет Si. 1. Критерий Лапласа Данный критерий предполагает равновероятность состояний внешней среды и рекомендует выбор стратегии с максимальным средним выигрышем: КЛ = Вероятности состояний природы Si равны между собой: 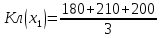 = 197; = 197;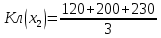 = 183; = 183;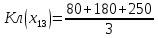 = 170; = 170;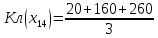 = 147. = 147.Следовательно, по критерию Лапласа рациональным будет производство при 4 АРМ. 2. Критерий Байеса Этот критерий учитывает вероятности состояний природы и рекомендует выбор стратегии с максимальным среднеожидаемым выигрышем: КБ = 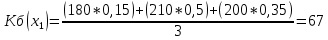 ; ;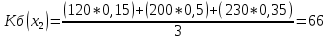 ; ;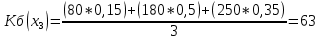 ; ;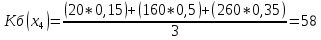 . .Следовательно, по критерию Байеса рациональным будет производство при 4 АРМ. 3. Критерий Вальда (максиминный критерий, критерий крайнего пессимизма, критерий наибольшей осторожности). Данный критерий ориентируется на худшее состояние внешний среды и рекомендует выбор стратегии с максимальным гарантированным выигрышем в таких условиях: КВ = Кв = 20. Следовательно, по критерию Вальда рациональным будет производство при 8 АРМ и потока заказов на обслуживание = 10. 4. Критерий Сэвиджа (минимаксного риска). Критерий минимаксного риска ориентируется на самую неблагоприятную обстановку и рекомендует выбор стратегии с минимальным риском: КС = Для использования данного критерия необходимо перейти от матрицы выигрышей к матрице рисков. Риск (rji) – разность между выигрышем, который игрок получил бы, если бы он знал, что состоянием природы будет состояние Si, и выигрышем, который игрок получит, не имея этой информации при использовании стратегии xj: Кс = 200. Следовательно, по критерию Сэвиджа рациональным будет производство при 4 АРМ и потока заказов на обслуживание = 30. 5. Критерий Гурвица (компромиссный критерий, критерий пессимизма-оптимизма). Этот критерий учитывает индивидуальные предпочтения сознательного игрока к пессимизму и оптимизму. Для его использования необходимо задать значение коэффициента пессимизма α, α КГ = КГ (х1) = 0,4*180 + (1-0,4)*200 = 192; КГ (х2) = 0,4*120 + (1-0,4)*230 = 186; КГ (х3) = 0,4*80 + (1-0,4)*250 = 182; КГ (х4) = 0,4*20 + (1-0,4)*260 =164 . Следовательно, по критерию Гурвица рациональным будет производство при 4 АРМ. Таким образом, рационально создание сервисного центра по обслуживанию и сопровождению своих изделий при АРМ = 4 и потоком заказов на обслуживание = 20. Задача 3. Динамично развивающаяся компания решила организовать клуб отдыха для своих сотрудников. Перед выбранными экспертами стоит задача выбора наилучшей альтернативы: - арендовать конный клуб; - арендовать гольф-клуб; - арендовать тренажерный зал; - арендовать бассейн (сауну). Определить наиболее предпочтительный вариант. Решение: При реализации экспертных процедур для участия в экспертизе привлечены 8 экспертов. Найдем веса целей методом предпочтения для случая: m = 8 и n = 4 (т.е. 8 эксперта и 4 целей). Исходная матрица предпочтений:
Модифицированная матрица предпочтения:
Суммарные оценки предпочтения: К1=12, К2=12, К3=13, К4=12 Искомые веса целей: ω1=12/49=0,24 ω2=12/49=0,24 ω3=13/49=0,265 ω4=12/49=0,24 Вывод: учитывая максимальное значение 3-го значения весов целей, самым оптимальным будет 3-ий вариант, а именно, обеспечить работников необходимой литературой. Заключение В заключении хотелось бы подчеркнуть, что риск сопровождает нас везде и всегда – на улице, на работе, дома. И, конечно, присутствует он и в бизнесе. И, так же как и в жизни, его не стоит избегать в предпринимательстве. Но тем более не стоит к нему стремиться, а наоборот, его нужно уметь просчитать и оценить. Только на основании объективных данных можно принимать какое-либо решение. Не рискуя, предприниматель ничего не добьется. Перед тем как начинать какое-нибудь дело, заключать сделку предприниматель должен все просчитать, продумать. Он должен рассчитать прибыль от данной затеи, вероятность успеха, или другими словами рассчитать риск сделки. Личные качества предпринимателя в итоге и определяют его склонность к риску. Некоторые из них предпочтут умеренную, но гарантированную прибыль, в то время как другие рискнут и, в случае успеха, получат прибыль в несколько раз большую, чем первая группа. Но у них всегда есть риск все потерять. В этом-то и заключается дилемма. Поэтому можно сказать, что одна из главных задач предпринимателя – оценить риск и свести его к минимуму, чтобы получить максимальную прибыль в случае удачной сделки, дела и понести минимальные потери в случае неудачной сделки. Риск можно снизить, распределив капитал по нескольким рисковым проектам, или, например, застраховав его. В рамках данной курсовой работы была рассмотрена тема «Имитационное моделирование». Имитационное моделирование — это метод исследования, при котором изучаемая система заменяется моделью с достаточной точностью описывающей реальную систему и с ней проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте). СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учебное пособие. –М.: Финансы и статистика, 2005. -426 с. Гинзбург А.И. Экономический анализ: Предмет и методы. Моделирование ситуаций. Оценка управленческих решений: учебное пособие. –СПб.: Питер, 2003. -622 с. Грабовый П.Г. Риски в современном бизнесе. –М.: Финансы и статистика, 2000. -200 с. Дубров А.М., Лагоша Б.А., Хрусталев Е.Ю. Моделирование рискованных ситуаций в экономике и бизнесе. –М.: Финансы и статистика, 2004. -224 с. Князевская Н.В., Князевский В.С. Принятие рискованных решений в экономике и бизнесе. –М.: Контур, 1998. -160 с. Кремер Н.Ш. Исследование операций в экономике. –М.: Банки и биржи, 2003. -407 с. Ларичев О.Н. Теория и методы принятия решений. –М.: Логос, 2006. -392 с. Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL. Практикум: Учебное пособие для вузов. –М.: ЗАО «Финстатинформ», 2000. -282 с. Синюк В.Г. Использование информационно-аналитических технологий при принятии управленческих решений: Учебное пособие. –М.: Экзамен, 2003. -237 с. Смородинский С.С., Батин Н.В. Методы и системы принятия решений. – часть 1 –Мн.: БГУИР, 2000. -329 с.; часть 2 –Мн.: БГУИР, 2001. -412 с. Трахтенгерц Э.А. Компьютерная поддержка принятия решений. –М.: СИНТЕГ, 2008. -270 с. Холод Н.И. Экономико-математические методы и модели. –Мн.: БГЭУ, 2000. -318 с. Чернов В.А. Анализ коммерческого риска. –М.: Финансы и статистика, 1998. -291 с. Шикин Е.В. Математические методы и модели в управлении. –М.: Финансы и статистика, 2002. -430 с. Эддоус М., Стэнсфилд Р. Методы принятия решений. – М.: ЮНИТИ, 1997. -425 с. Экономико-математические методы и модели: Учебное пособие / под ред. Холод Н.И., Кузнецова А.В., Жихар Я.Н. и др. – Мн.: БГЭУ, 2000. -385 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
