|
|
Контрольная работа по математике 1 семестр. Контр.1. Контрольная работа по дисциплине Высшая математика (часть 1 ) Контрольная работа 1 Выполнил Журавлев Д. Д. Группа мит22
Федеральное агентство связи
Сибирский государственный университет телекоммуникаций и информатики
Межрегиональный учебный центр переподготовки специалистов
Контрольная работа
по дисциплине: Высшая математика (часть 1 )
Контрольная работа 1
Выполнил: Журавлев Д.Д.
Группа: МИТ-22
Вариант: 1
Проверила: Храмова Татьяна
Викторовна
Новосибирск, 2022 год.
Задание 1. Матричная алгебра
 Решить систему линейных уравнений методом Крамера. Решить систему линейных уравнений методом Крамера.
3x + 2y + z = 5,
2x + 3y + z =1,
2x +y + 3z = 11.
 Решение. Запишем систему уравнений в матричном виде: Решение. Запишем систему уравнений в матричном виде:
   3x + 2y + z = 5, 3 2 1 x 5 3x + 2y + z = 5, 3 2 1 x 5
2x + 3y + z =1, 2 3 1 • y = 1 ,
   2x +y + 3z = 11. 2 1 3 z 11 2x +y + 3z = 11. 2 1 3 z 11
3 2 1 5 x
A = 2 3 1 , B = 1 , X = y .
2 1 3 11 z
 Найдём определитель матрицы A: Найдём определитель матрицы A:
3 2 1
= |A| = 2 3 1 = 3 ∙ 3 ∙ 3 + 2 ∙ 1 ∙ 1 + 2 ∙ 1∙ 2 2 ∙ 3 ∙ 1 1 ∙ 1 ∙ 3 2 ∙ 2 ∙ 3 =
2 1 3
= 27 + 2 + 4 6 3 12 = 12
   Найдём определители матриц, полученных из матрицы A заменой i-го столбца на столбец B правых частей (i=1,2,3): Найдём определители матриц, полученных из матрицы A заменой i-го столбца на столбец B правых частей (i=1,2,3):
5 2 1 3 5 1 3 2 5
x = 1 3 1 = 24, y = 2 1 1 = 24, z = 2 3 1 = 36.
11 1 3 2 11 3 2 1 11
Подставим полученные значения в формулы Крамера и найдём решение системы:
x = 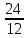 = 2, y = = 2, y = 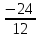 = 2, z = = 2, z = 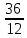 = 3. = 3.
Ответ: x = 2, y = 2, z = 3.
Задание 2. Аналитическая геометрия
Даны четыре точки в пространстве: A(0;0;0), B(1;1;0), C(0;1;0), D(1;2;1).
Составить уравнение прямой АВ и плоскости BCD, вычислить угол между ними и расстояние от точки А до плоскости BCD.
Решение. Уравнение прямой, проходящей через две точки (xi, yi, zi), i=1,2 имеет вид:
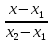 = = 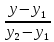 = = 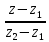 . .
Подставим в уравнение значения координат точек A(0;0;0), B(1;1;0) и преобразуем выражение:
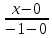 = = 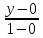 = = 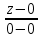 , ,
 = = 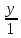 = = 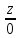 — канонические уравнения прямой AB. — канонические уравнения прямой AB.
В знаменателях канонических уравнений прямой указаны координаты направляющего вектора
прямой: q (1;1;0).
 Уравнение плоскости, проходящей через три точки (xi, yi, zi), i=1,2,3 имеет вид: Уравнение плоскости, проходящей через три точки (xi, yi, zi), i=1,2,3 имеет вид:
x 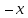 1 1 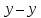 1 1 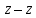 1 1
 2 2 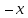 1 1 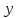 2 2 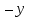 1 1 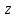 2 2 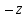 1 = 0 . 1 = 0 .
 3 3 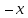 1 1 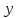 3 3 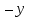 1 1 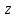 3 3 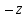 1 1
  Подставим в уравнение значения координат точек B(1;1;0), C(0;1;0), D(1;2;1) и преобразуем выражение: Подставим в уравнение значения координат точек B(1;1;0), C(0;1;0), D(1;2;1) и преобразуем выражение:
x + 1 y 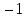 z z 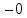 x + 1 y x + 1 y  1 z 1 z 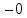
0 + 1 1 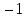 0 0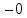 = 0 1 0 0 = 0 = 0 1 0 0 = 0
1 + 1 2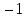 1 1 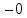 2 1 1 2 1 1
   Вычислим определитель (формула «по первой строке»): Вычислим определитель (формула «по первой строке»):
0 0 1 0 1 0
(х 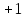 ) ) 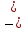 у у 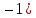 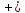 z = 0 , z = 0 ,
1 1 2 1 2 1
0 ∙ ( x+1 ) 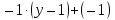 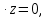
0 ∙ x 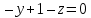
0 ∙ x 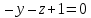 — уравнение плоскости BCD. — уравнение плоскости BCD.
Коэффициенты перед переменными – координаты нормали к плоскости 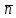 (0; (0; 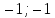 ) . ) .
Угол между плоскостью и прямой можно найти, зная нормаль плоскости и
направляющий вектор прямой:
sin =  = =  = =  = =
= 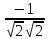 = = 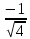 = = 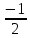 , ,
Найдём значение угла : = arcsin 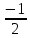 . .
Знак «—» следует проигнорировать, так как указывая угол между плоскостью и прямой, принято указывать острый: = arcsin 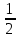 . .
Расстояние от точки до плоскости — это проекция произвольного вектора, соединяющего плоскость и точку на нормаль этой плоскости:
d (A, BCD) =  = = 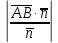 = = 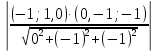 = =
= 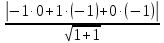 = = 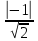 = = 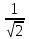
Ответ: 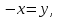 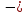 y y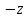 + 1 = 0 , arcsin + 1 = 0 , arcsin 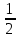 , , 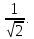
Решение_2-ым_способом_(правила_Лопиталя).'>Задание 3. Предел функции
Вычислить пределы отношения величин.
Решение 2-ым способом (правила Лопиталя).
a) 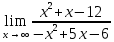 = = 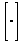 = = 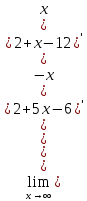 = = 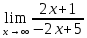 = =
= 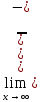 = = 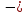 . .
Ответ: 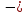 . .
Решение 1-ым способом (преобразование выражения, сведение к первому замечательному пределу).
б)  = =  = =  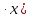 = 2 = 2 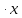 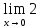 = 2 . = 2 .
Ответ: 2 .
Задание 4. Исследование функции
Дана функцияy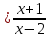
Требуется провести её полное исследование и построить график.
Решение. Исследование будем проводить по следующей схеме:
1. Найти область определения функции.
2. Найти точки пересечения графика с осями координат.
3. Выяснить, является ли функция чётной, нечётной, периодической или общего вида.
4. Найти точки разрыва функции и определить их характер.
5. Найти асимптоты функции.
6. Найти интервалы монотонности и экстремумы функции.
7. Найти интервалы выпуклости и точки перегиба графика функции.
8. Построить эскиз графика.
1. Знаменатель не может быть равен 0, поэтому функция не определена при
х ≠ 2 и х = − 1 . То есть область определения состоит из двух интервалов
( −∞, 2) ∪ ( 2, ∞), а график, соответственно, из двух ветвей.
Функция знакоположительна ( y 0) в интервалах ( −∞, − 1) и (2, +∞), знакоотрицательна ( y 0) в ( −1, +∞).
2. Если x = 0, то y = − 0,5 . То есть график функции не пересекается с осями координат.
3. Функция не является периодической. Проверим на чётность:
y(−x) 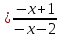 = y(x). = y(x).
Таким образом, функция является чётной, следовательно, её график не симметричен относительно начала координат. Для построения графика достаточно провести исследование при x < −2 и х > 2.
4. В точке x 2 функция имеет разрыв второго рода:
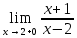 = +∞ ; = +∞ ; 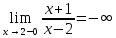 . .
5. Прямая х = 2 является вертикальной асимптотой. Выясним наличие наклонной y = kx+b:
k = 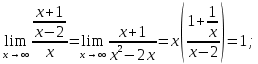
b = 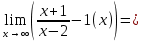 ∞. ∞.
При х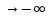 также k = 1 и b = также k = 1 и b = 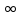 . Следовательно, y x —горизонтальная асимптота. . Следовательно, y x —горизонтальная асимптота.
6. Исследуем функцию на экстремумы.
у= = =  = =  . .
y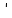 = 0 при х1 = 2 . Исследуем интервалы знакопостоянства первой производной: = 0 при х1 = 2 . Исследуем интервалы знакопостоянства первой производной:
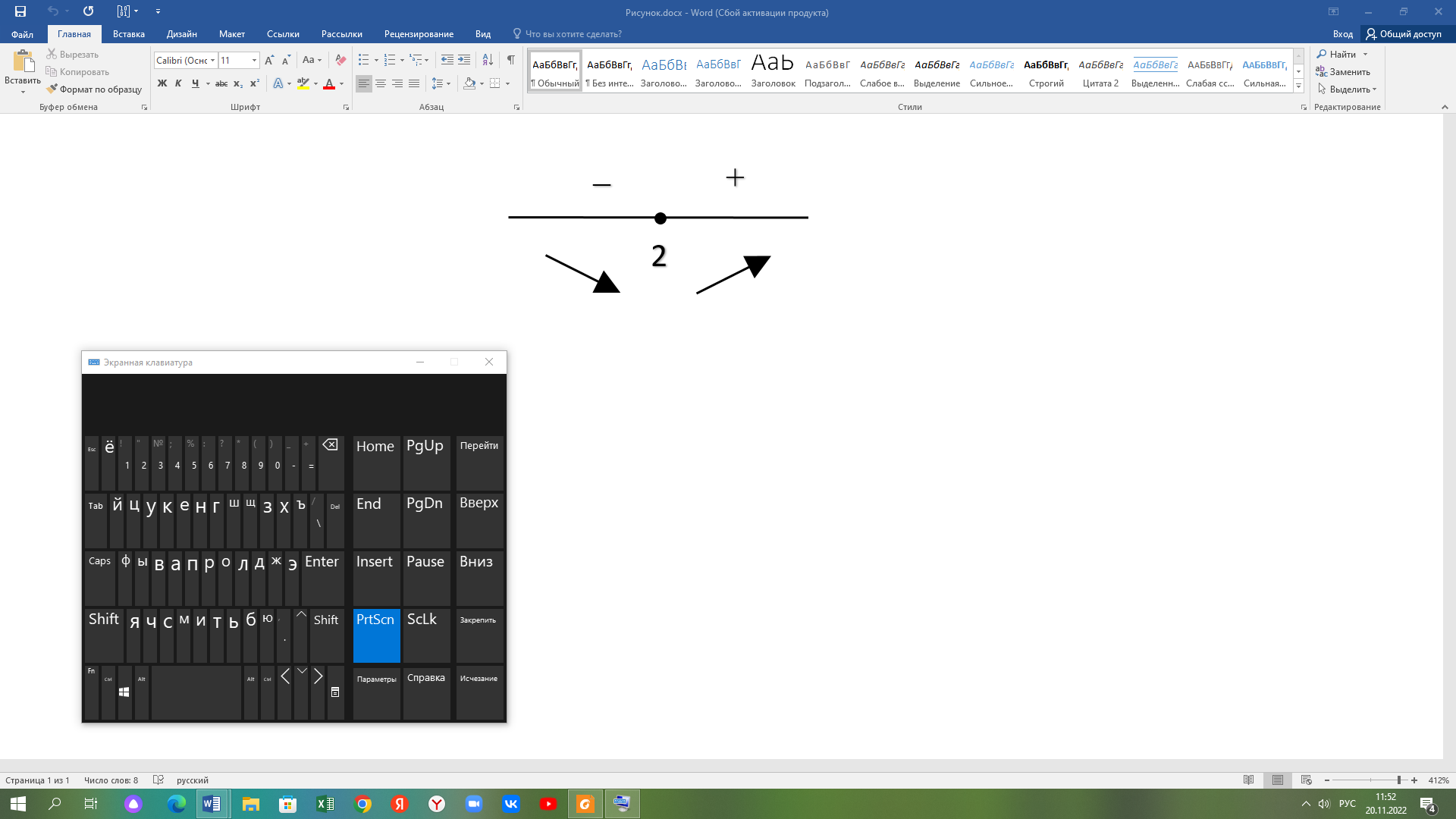
Рис. 1 – точки экстремума и монотонность
Функция убывает на промежутке ( −∞, 2) , на всех остальных интервалах области определения она возрастает (Рис. 1).
7. Исследуем функцию на выпуклость. Находим y:
y = 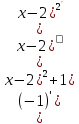 = = 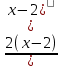 = = 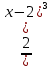
Вторая производная равна нулю или не существует в точке х1 = 2 :

Рис. 2 – точки перегиба и выпуклость
Точка (0, 0) – точка перегиба. На интервале ( −∞, 2) график выпуклый, на (2,+ ∞) – вогнутый (Рис. 2).
8. Используя полученные данные, рисуем эскиз графика заданной функции (Рис. 3):
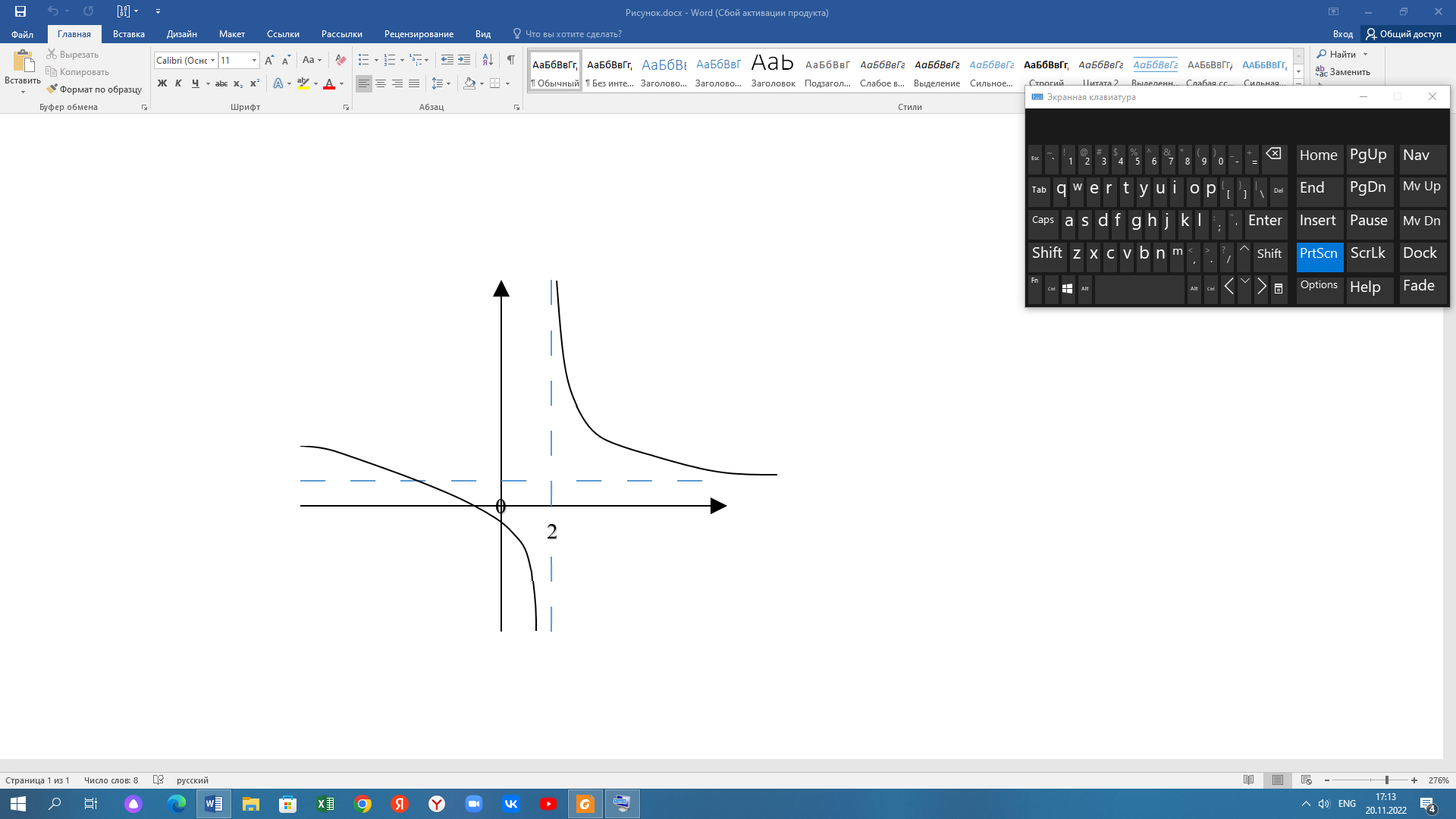
Рис. 3 – эскиз графика функции
Задание 5. Интеграл
Если фигура ограничена сверху кривой yв. (x) , а снизу yн. (x) при a x b , то её площадь вычисляется по формуле
S = 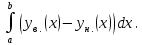
Вычислить площадь фигуры, ограниченной линиями:
y = 3x2 + 1 ; y = 3x + 7.
Решение. Построим чертёж (Рис. 1) и определим ограничения.
Найдём точки пересечения кривых:
 y = 3x2 + 1 y = 3x2 + 1
3x2 + 1 = 3x + 7 3x2  3x 3x  6 = 0 x2 6 = 0 x2  x x 2 = 0 2 = 0
y = 3x + 7 x1 = 2 , x2 = 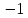 ; ;
 Рис. 1 Рис. 1
S =  = = 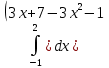 = =
= 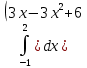 = = 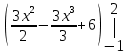 = =  = =
= 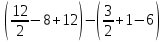 = 10 + 3,5 = 13,5. = 10 + 3,5 = 13,5.
Ответ: 13,5.
Задание 6. Функции двух переменных
Исследовать на экстремум функцию двух переменных z = f(x, y).
Функция: z = xy + y2  2x . 2x .
Решение. Найдём частные производные функции z:
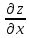 = (xy + y2 = (xy + y2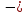 2x) 2x) y y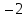 , , 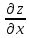 = (xy + y2 = (xy + y2 2x) 2x)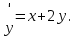
 Найдём стационарные точки функции z: Найдём стационарные точки функции z:
 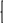 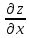 = 0 = 0
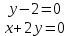 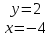
 = 0 = 0
Вычислим вторые производные функции в точке (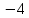 ;2): ;2):
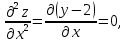  
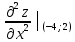 = 0, = 0, 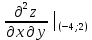 = 1, = 1,  . .
Стационарную точку характеризует определитель :
= 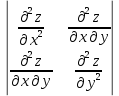 = = 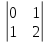 = = 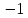 . .
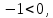 экстремума нет. экстремума нет.
Точка (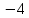 ;2) является седловой. ;2) является седловой.
Ответ: (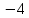 ;2) — седловая точка. ;2) — седловая точка. |
|
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.