высшая математика. Контрольная работа по высшей математике (часть 1). Контрольная работа По дисциплине Высшая математика (часть 1) Выполнил Попов Сергей Александрович
 Скачать 298 Kb. Скачать 298 Kb.
|
|
Федеральное агентство связи Сибирский Государственный Университет Телекоммуникаций и Информатики Межрегиональный центр переподготовки специалистов Контрольная работаПо дисциплине: Высшая математика (часть 1)Выполнил: Попов Сергей Александрович Группа: ИСТ-92 Вариант: 01 Проверил: ___________________ Новосибирск, 2019 г Оглавление Задание 1. Матричная алгебра…………………………………………………..3 Решить систему уравнений методом Крамера 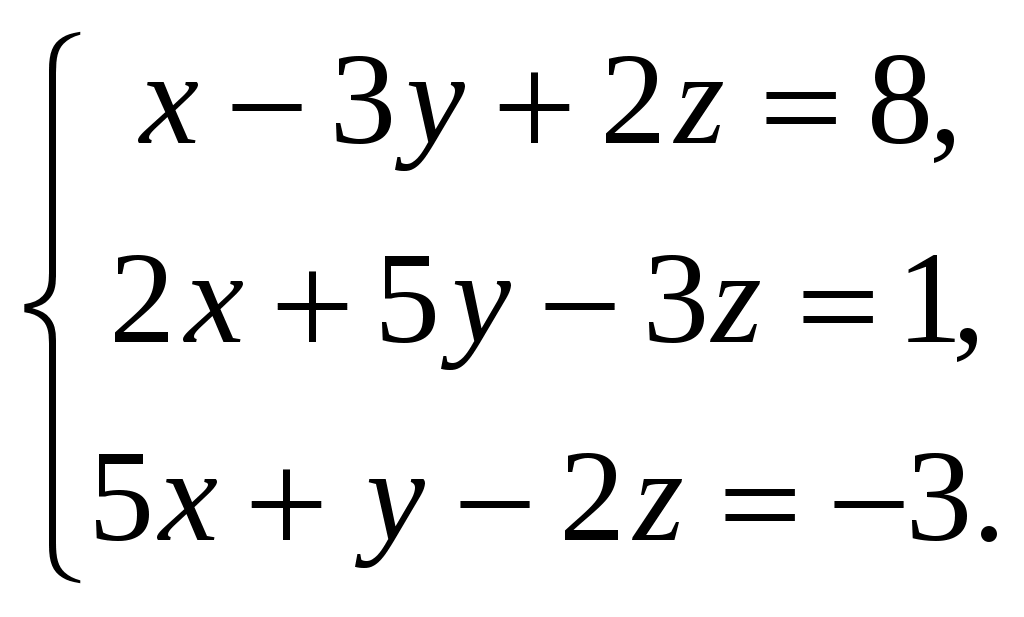 Задание 2. Аналитическая геометрия…………………………………………..4 По заданным точкам A (0;0;0), B (-1;1;0), C (0;1;0), D (1;2;1) составить уравнения прямой АВ и плоскости BCD, вычислить угол между ними и найти расстояние от точки А до плоскости BCD. Задание 3. Предел функции……………………………………………………..4 Вычислить предел отношения величин 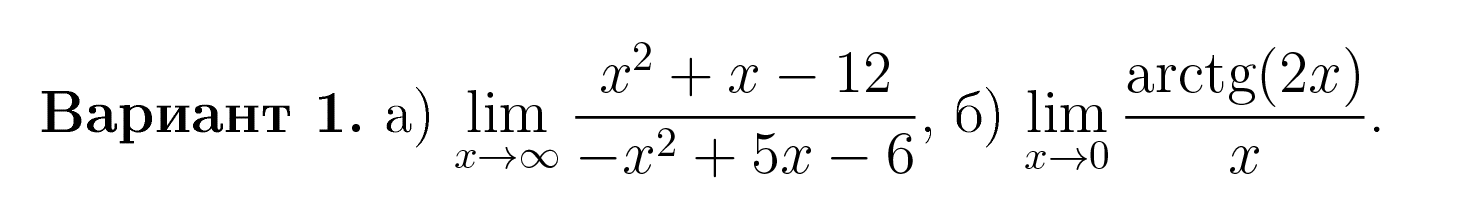 Задание 4. Исследование функции……………………………………………..5 Исследовать функцию и построить эскиз графика Задание 5. Интеграл……………………………………………………………..7 Вычислить площадь плоской фигуры, ограниченной линиями Задание 6. Функции двух переменных…………………………………………8 Исследовать на экстремум функцию двух переменных Задание 1. Матричная алгебра. Решить систему уравнений методом Крамера. 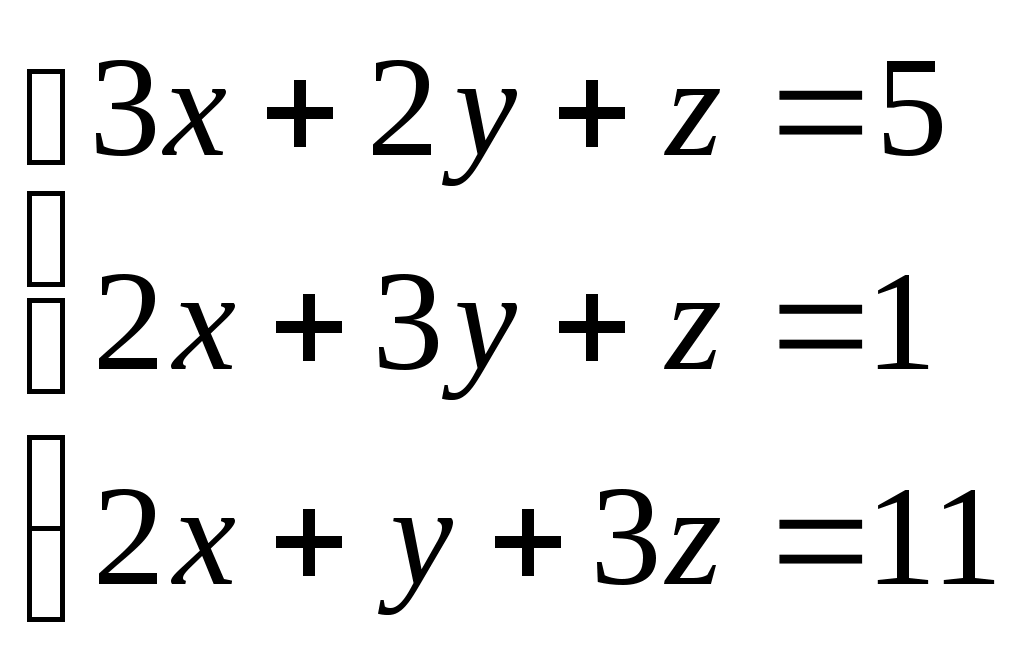 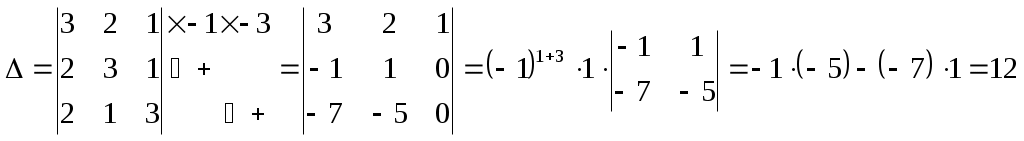 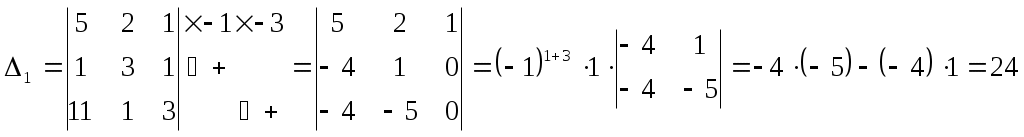 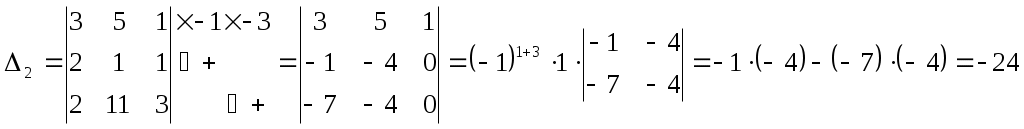 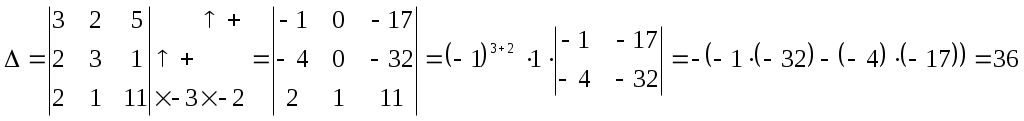 Решение системы: 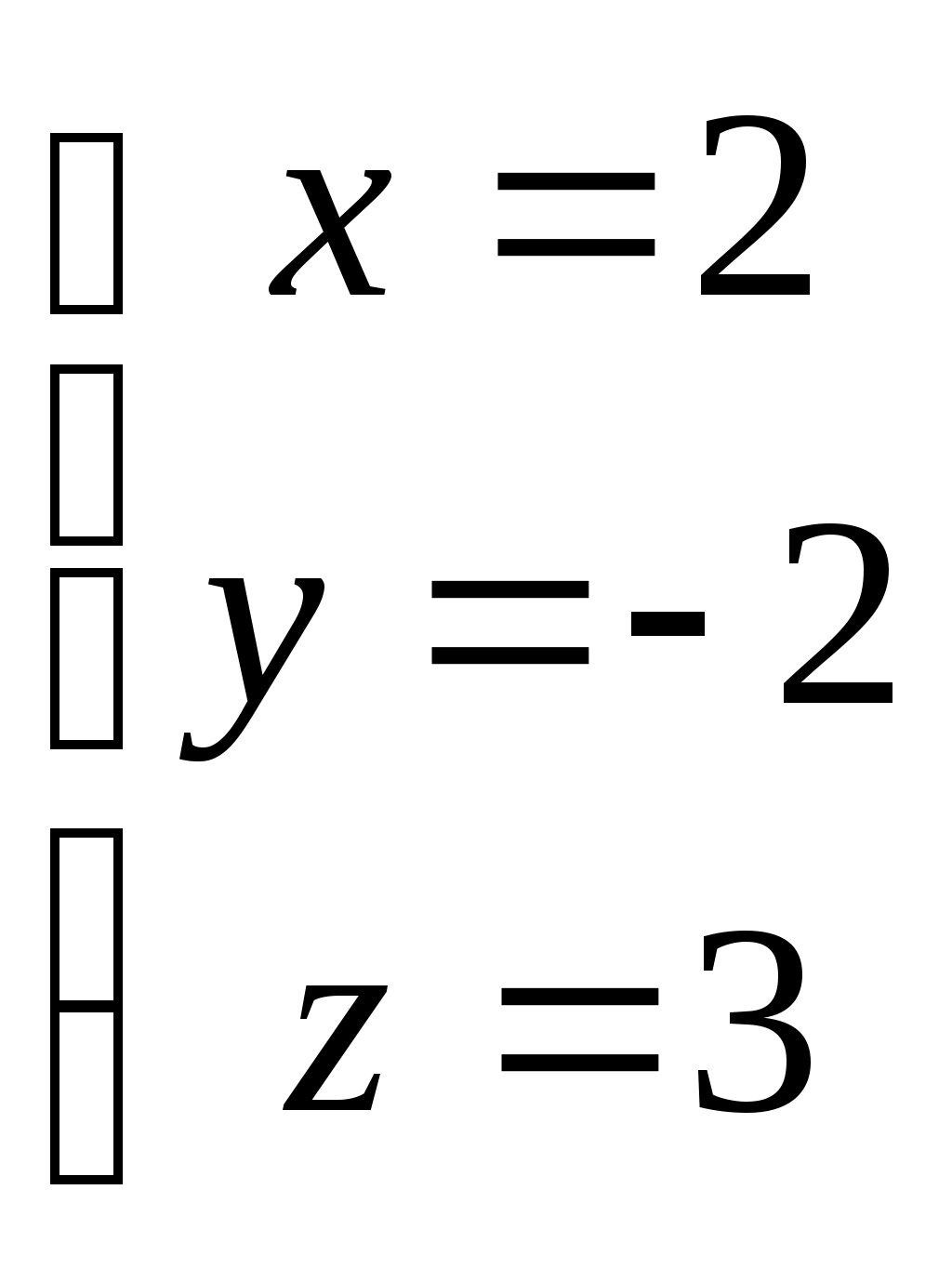 Проверка: Проверка: 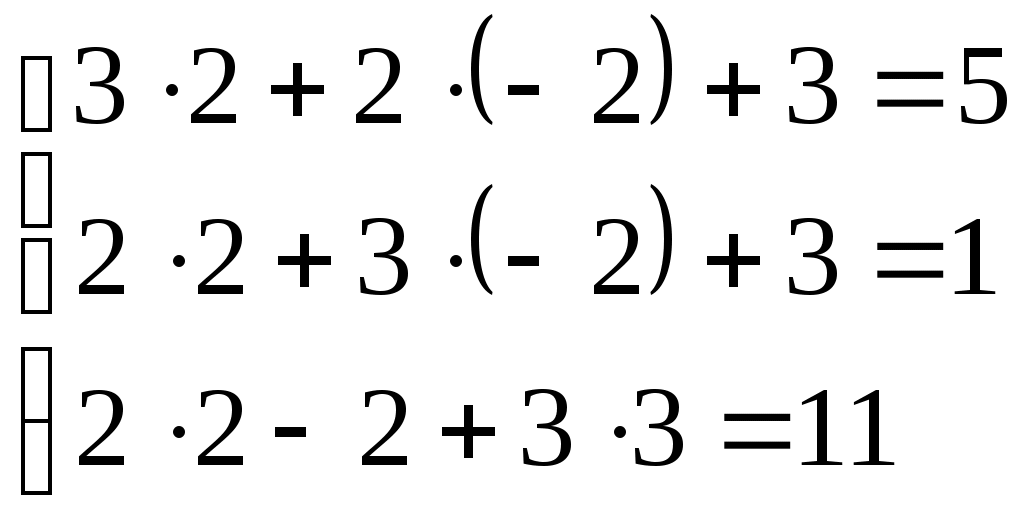 – верно. – верно. Задание 2. Аналитическая геометрия. По заданным точкам A (0;0;0), B (-1;1;0), C (0;1;0), D (1;2;1) составить уравнения прямой АВ и плоскости BCD, вычислить угол между ними и найти расстояние от точки А до плоскости BCD. Уравнения прямой АВ: Уравнение плоскости 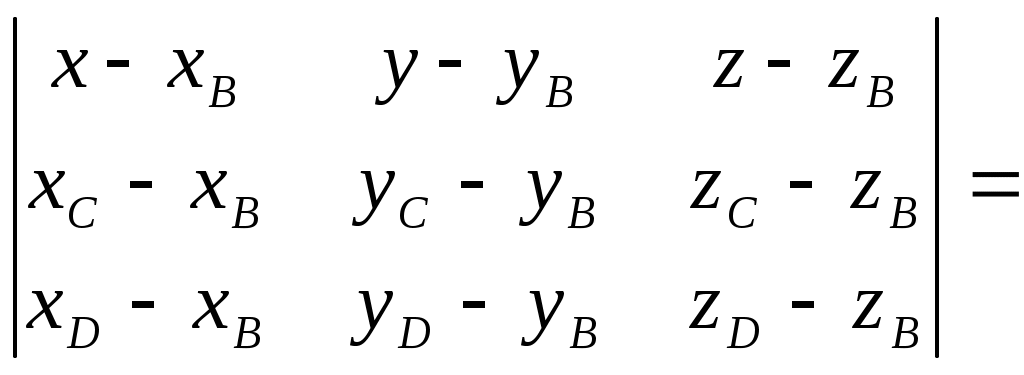 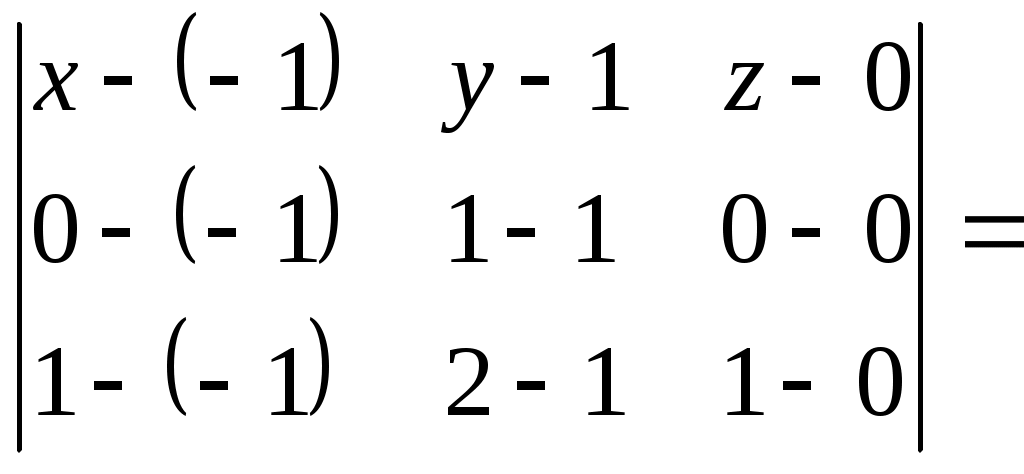 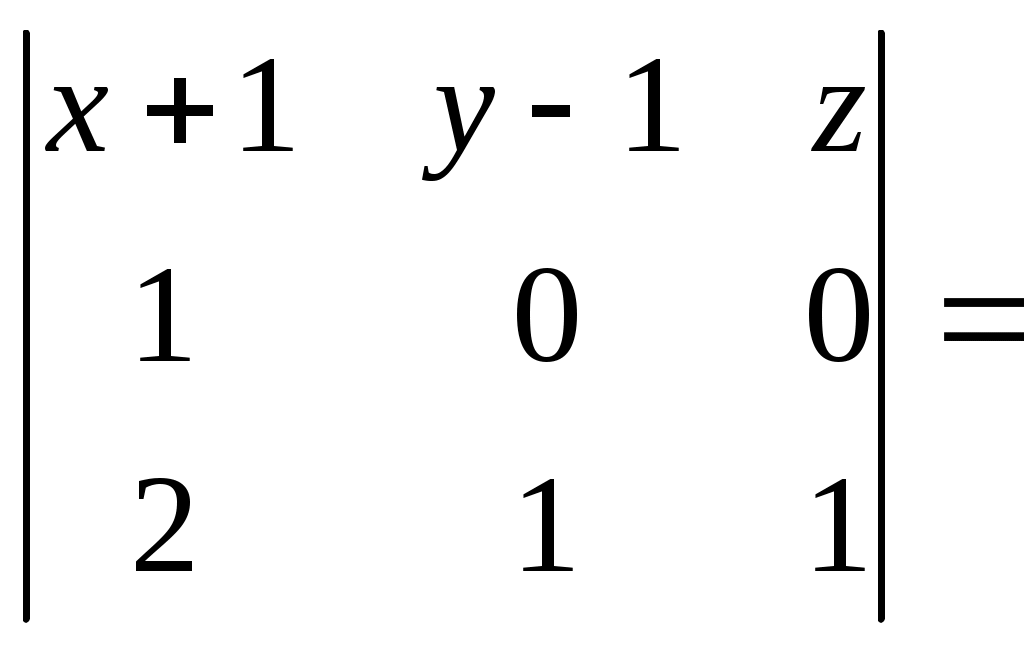 Угол между прямой АВ и плоскостью Расстояние от точки А до плоскости BCD: 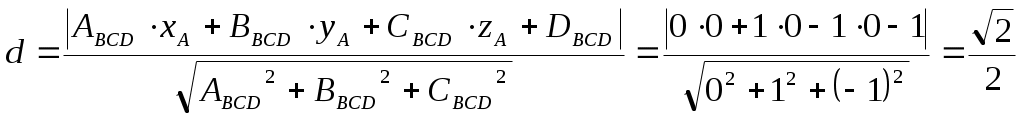 Задание 3. Предел функции Вычислить предел отношения величин а) 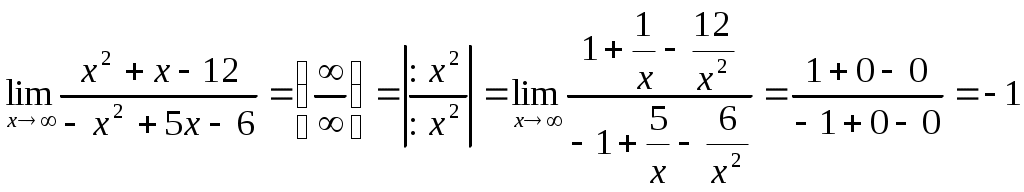 б) Задание 4. Исследование функции Исследовать функцию и построить эскиз графика 1) Точка, в которой функция не определена: Область определения: 2) 3) Точки пересечения с осью Ох: Точка пересечения с осью Оу: 4) Функция – непериодическая, разрывная. 5) Наклонные асимптоты вида y = kx + b: 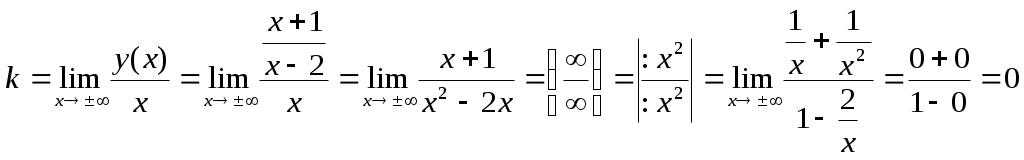 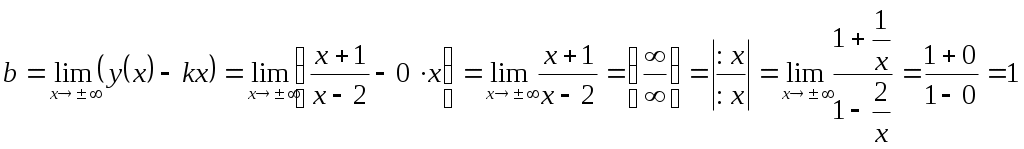 у=1 – горизонтальная асимптота. 6) Экстремумы, монотонность: 7) Перегибы, выпуклость: ни при каких х из области определения. Перегибов нет. Поведение функции и второй производной на интервалах:
Интервалы выпуклости: (-∞;2); вогнутости: (2; ∞). 8) График: 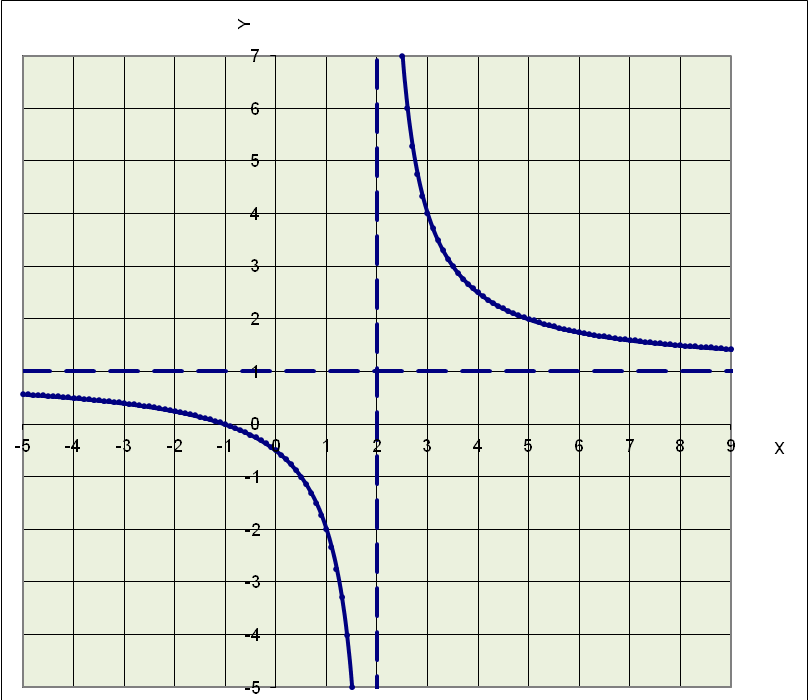 Задание 5. Интеграл Вычислить площадь плоской фигуры, ограниченной линиями 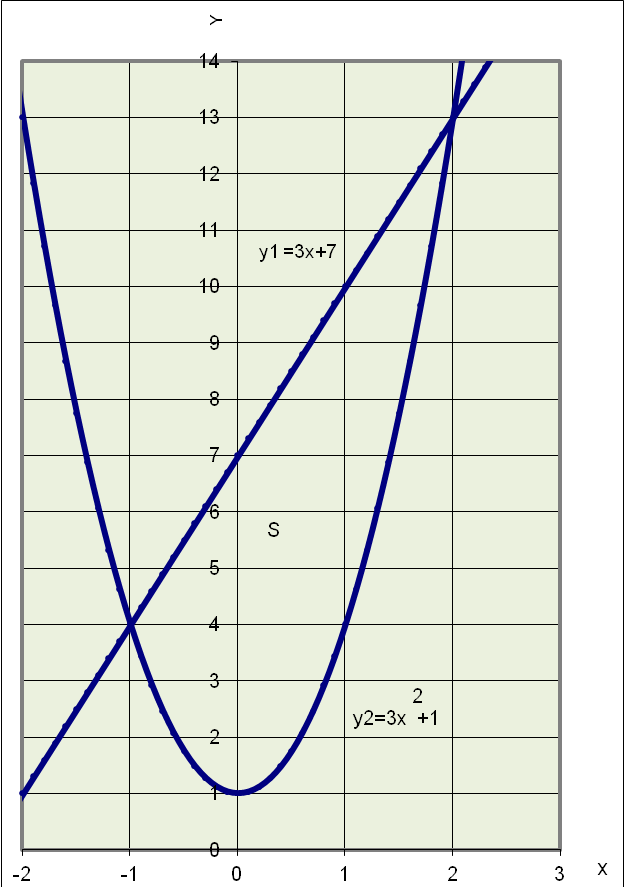 Точки пересечения линий: Искомая площадь фигуры: 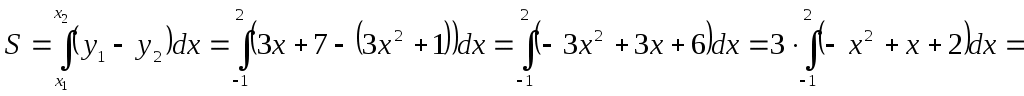 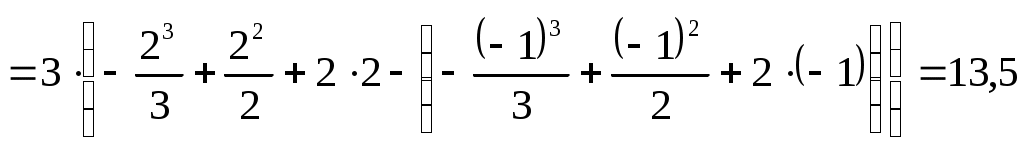 (кв.ед.) (кв.ед.)Задание 6. Функции двух переменных Исследовать на экстремум функцию двух переменных Необходимое условие существования экстремума – равенство частных производных нулю: 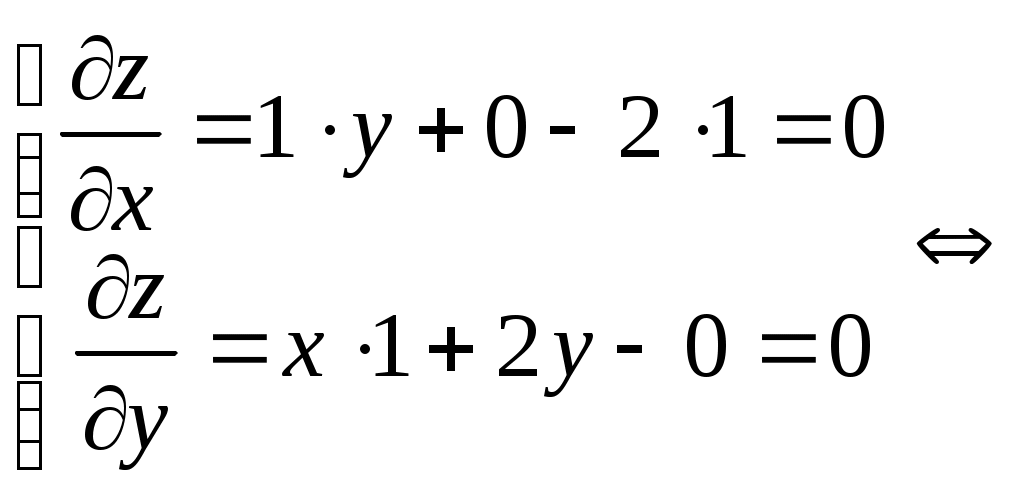 В точке По критерию Сильвестра: |
