Явление переноса импульса 10 вариант. КР(Явление переноса импульса10 вариант. Контрольная работа по дисциплине Явление переноса импульса и энергии в химической технологии Вариант 10
 Скачать 161.83 Kb. Скачать 161.83 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный технический университет» Контрольная работа по дисциплине «Явление переноса импульса и энергии в химической технологии» Вариант № 10 Выполнил студент группы : Проверил Волгоград 2023 г. Задача № 1 Определить режим течения жидкости в межтрубном пространстве теплообменника типа «труба в трубе» при следующих условиях: 1) массовый расход жидкости Q = 3890 кг/час; 2) диаметр внутренней трубы теплообменника d = 20×2 мм; 3) диаметр внешней трубы теплообменника D = 55×2 мм; 4) плотность жидкости ρ = 1150 кг/м3; 5) динамический коэффициент вязкости жидкости, μ=1,2×10-3 Па∙с. Решение. Скорость жидкости ν определим из уравнения расхода: 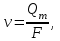 где Qm – массовый расход жидкости, кг/с; F – площадь поверхности, м2, 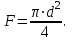 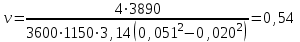 м/с. м/с.Эквивалентный диаметр кольцевого сечения определяем по формуле: 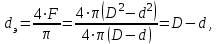 где D – внутренний диаметр наружной трубы, м; d – наружный диаметр внутренней трубы, м. 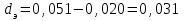 м. м.Динамический коэффициент вязкости жидкости μ=1,2×10-3 Па∙с. Критерий Рейнольдса: 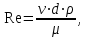 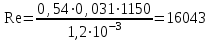 Режим турбулентный. Задача № 2 По трубам одноходового кожухотрубчатого теплообменника проходит воздух при средней температуре Т = 48 0С и давлении (по манометру) рман = 3,0 кгс/см2 , со скоростью ν = 4 м/с. Барометрическое давление 740 мм. рт.ст. Наружный диаметр труб 20 мм, толщина стенки 2,5 мм. Число труб n = 70. Определить: Массовый расход воздуха; Объемный расход воздуха при рабочих условиях; Объемный расход воздуха при нормальных условиях. Решение Плотность воздуха при нормальных условиях ρо = 1,293 кг/м3. Рабочее давление (абсолютное): 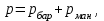 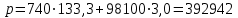 Па. Па.Плотность воздуха при рабочих условиях: 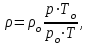 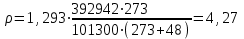 кг/м3. кг/м3.Массовый расход воздуха рассчитаем по уравнению:  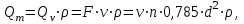 где ν – средняя скорость потока, м/с; ρ – плотность газа, кг/м3; d – внутренний диаметр трубы, м, F– площадь поперечнего сечения, м2. 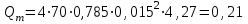 кг/с. кг/с.Объемный расход воздуха при рабочих условиях: 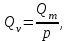 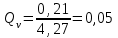 м3/с. м3/с.Объемный расход воздуха, приведенный к нормальным условиях:  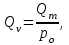 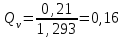 м3/с. м3/с.Задача № 3 Движение хлористого водорода в трубопроводе d1=450 мм при 4500С изучается на модели (масштаб 1:10), через которую продувается воздух при 25 0С. Хлористый водород движется по трубопроводу при помощи газодувки со скоростью ν1 = 4 м/с, плотностью газа ρ1 = 0,569 кг/м3, вязкость μ1 = 0,0333∙10-3 Па∙с. Определить: 1) Условия гидродинамического подобия в трубопроводе и модели; 2) Скорость, с которой надо продувать воздух в модели для того, чтобы воспроизвести в ней движение газа в трубопроводе. Решение Так как движение в трубопроводе вынужденное, то достаточным условием подобия является равенство критерия Рейнольдса: 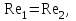 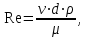 где, ν – средняя скорость потока, м/с; d – диаметр трубопровода, м; ρ – плотность жидкости, кг/м3; μ- динамическая коэффициент вязкости, Па∙с. 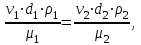 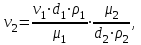 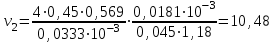 м/с. м/с.Задача № 4 Мерник диаметром D = 1,2 м и высотой H = 2,0 м освобождается через отверстие в боковой стенке. Диаметр отверстия d = 15 мм, ось его находится на высоте h = 40 мм от днища мерника. Мерник сообщается с атмосферой, его начальная степень заполнения β = 0,85. Тип отверстия: короткий цилиндрический патрубок. Определить продолжительность полного истечения жидкости из мерника. Решение Определяем начальную высоту столбца вытекающей жидкости в мернике над осью штуцера: 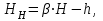 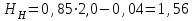 м, м,Воспользуемся формулой: 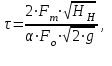 где Fm- площадь сечения сосуда, м2; Fo – площадь отверстия, м2; H – начальная скорость уровня, м; α – коэффициент расхода (справочная величина, для короткого цилиндрического патрубка принимаем α = 0,82)[1]. 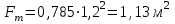 , ,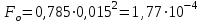 м2, м2,Продолжительность полного истечения жидкости из мерника: 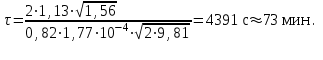 Задача № 5 Вычислить значения скоростей движения в прямой трубе диаметром D = 50×2,5 мм, при которых потоки перестают быть ламинарными для: 1) газа О2 при ратс = 1 атм и температуре Т = 40 0С; 2) для нефтяного масла, имеющего динамическую вязкость μ = 35,9∙10-3 Па∙с, плотность нефтяного масла ρ= 940 кг/м3 Решение Критическая скорость будет иметь место при Reкр = 2300; из уравнения: 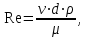 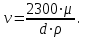 где ν – средняя скорость потока, м/с; d – диаметр трубопровода, м; ρ – плотность жидкости, кг/м3; μ- динамический коэффициент вязкости, Па∙с. 1) для газа О2: 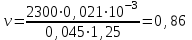 м/с, м/с,где 0,021 - динамический коэффициент вязкости при 40 0С, мПа∙с; 1,25 кг/м3 - плотность газа О2 при 20 0С, рассчитанный по формуле: 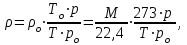 где ρо = М/22,4 кг/м3 - плотность газа при нормальных условиях; Т– температура, К; М – мольная масса газа О2, кг/гмоль;. 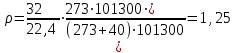 кг/м3. кг/м3.2) для нефтяного масла: 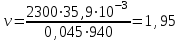 м/с. м/с.Задача № 6 На трубопроводе имеется переход с диаметра d1= 75 мм на диаметр d2= 95 мм (диаметры внутренние). По трубопроводу движется вода, имеющая температуру 20 оС. Её скорость в узком сечении ν1 = 1,6 м/с. Определить: 1) объёмный и массовый расходы воды; 2) скорость воды в широком сечении ν2; режимы течения в узком и широком сечениях. Решение Из уравнение неразрывности потока следует: 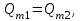 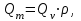 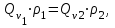 => =>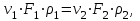 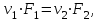 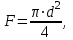 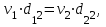 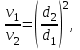 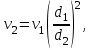 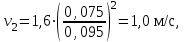 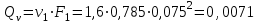 м3/с, м3/с,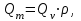 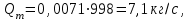 Находим критерий Рейнольдса: 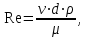 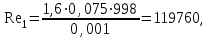 режим течения жидкости турбулентный. 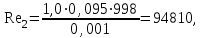 режим течения жидкости турбулентный. Задача № 7 Труба диаметром d1 = 240×10 мм переходит в трубу диаметром d2 = 75×5 мм, после чего поднимается вверх на h = 14 м. В нижнем и верхнем сечениях трубы установлены манометры. Нижний манометр показывает давление Р1 = 5,5 кГс/см2. По трубопроводу перекачивается вода с расходом Q = 65 м3/час и температурой t = 34 oC. Определить показания верхнего манометра Р2 кГс/см2. Наличием сил вязкости пренебречь. Решение Сумма геометрического и динамического напора есть величина постоянная во всех сечениях потока для идеальных жидкостей. Уравнение Бернули: 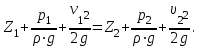 Скорость потока найдем через уравнение неразрывности: 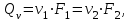 => => 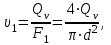 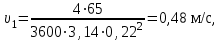 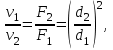 => => 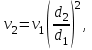 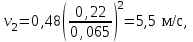 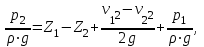 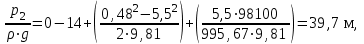 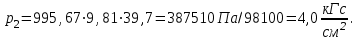 Показание верхнего манометра Р2 = 4,0 кГс/см2   Задача № 8 По трубопроводу длиной L = 19 км и диаметром D = 135×5 мм перекачивается бензол с расходом Q = 14 т/час при средней температуре 20оС. Стенки трубопровода гладкие. Манометр, установленный в начале, показывает давление Р1 = 7,5 атм. Определить показание манометра Р2, установленного в конце трубопровода. Решение Из уравнения массового расхода жидкости, можно определить скорость потока жидкости ν: 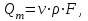 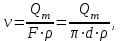 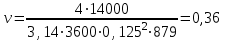 м/с, м/с,Динамический коэффициент вязкости жидкости μ = 0,65×10-3 Па∙с. Критерий Рейнольдса: 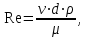 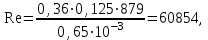 режим турбулентный. Потерю давления на трение определяем по формуле:  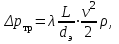 где λ – коэффициент трения, безмерный (его значение зависит в общем случае от режима течения и шероховатости стенки трубы е); ρ – плотность жидкости, кг/м3; d – диаметр трубы, м; L – длина трубы, м; ν – скорость потока, м/с. Определяем коэффициент трения λ по формуле Бразиуса: 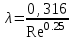 , ,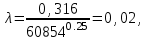 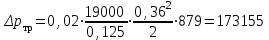 Па∙с Па∙с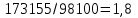 кГс/см2, кГс/см2,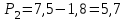 кГс/см2. кГс/см2.Показание манометра Р2 = 5,7 кГс/см2 Задача № 9 Определить максимальную и среднюю скорости воздуха, его объемный расход при рабочих и нормальных условиях, массовый расход при следующих исходных данных: - давление в трубопроводе атмосферное; - диаметр трубопровода D = 76*3 мм; - температура воздуха = 400 С; - показания водяного дифманометра, подключенного к трубке Пито-Прандтля, составляет h = 10 мм. Трубка Пито-Прандтля установлена вдоль оси воздухопровода. Решение. Плотность воздуха при t = 400 С: 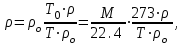 где ρо = М/22,4 кг/м3 - плотность газа при нормальных условиях; Т– температура, К; М – мольная масса воздуха, кг/гмоль. 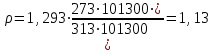 кг/м3. кг/м3.Максимальная (осевая) скорость воздуха определяется из выражения: 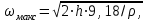 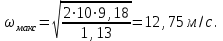 Этой скорости соответствует значение критерия Рейнольдса: 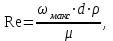 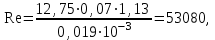 режим турбулентный режим турбулентныйгде 0,019∙10-3 - μ- динамический коэффициент вязкости, Па∙с, определяем по номограмме (рис. VI) [1]. По рис.1.2 [1] для Re = 53080 отношение средней скорости к максимальной 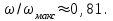 Средняя скорость: 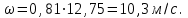 Расход воздуха: 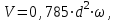 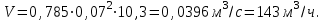 пересчёт на нормальные условия: 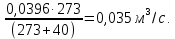 Массовый расход воздуха: 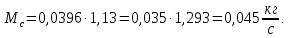 Задача № 10 Вычислить потерю давления на преодоление сил трения при прохождении воды по змеевику со скоростью ν = 1,0 м/с при t = 300 С. Диаметр стальной трубы с незначительной коррозией D = 51*2,5 мм. Число витков n = 10, диаметр витков d = 1,2 м. Решение Определяем режим течения. Динамический коэффициент вязкости воды при t = 300 С равен 0,8 мПа (табл. VI). Критерий Рейнольдса: 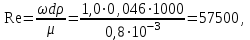 режим турбулентный. режим турбулентный.Для цельнотянутой стальной трубы с незначительной коррозией, среднее значение шероховатости стенок трубы е = 0,2 мм (табл. XII) [1], тогда: 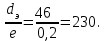 По графику (рис. 1.5) при Re = 57500 и dэ/e = 230 находим λ 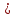 0,029. 0,029.Приближенно длина змеевика равна: 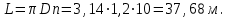 Потерю давления на трение для прямой трубы находим по формуле: 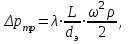 где λ – коэффициент трения; dэ – эквивалентный диаметр трубы (dэ=d), м; L – длина трубы, м; ω – скорость потока, м/с; ρ – плотность жидкости, кг/м3. 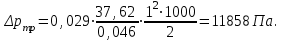 Находим поправочный коэффициент по формуле: 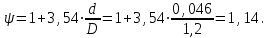 Следовательно, для змеевика: 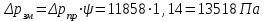 или 1378 мм вод.ст. |
