Термех. Контрольная работа по электротехнике Руководители Яковлев В. А. студентка группы пс286 Левшунова Ю
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
|
Федеральное агентство образования и науки Российской Федерации Южно-Уральский государственный университет Кафедра системы управления  Контрольная работа ПО ЭЛЕКТРОТЕХНИКе Руководители: Яковлев В.А. Выполнила: студентка группы ПС-286 Левшунова Ю. ______________ Работа защищена на оценку____ "___",_______________2007г Челябинск, 2007 Контрольное задание №1 "Расчет цепей постоянного тока"Задача 1. В схеме (рис.1) R1 = 2 Ом, R2 = 3 Ом, R5 = 2 Ом, I3 = 1,5 A. Остальные исходные данные приведены в таблице 1. На схемах показаны принятые положительные направления токов в ветвях; номера токов соответствуют номерам ветвей. Пользуясь законами Кирхгофа и законом Ома, определить все неизвестные токи и сопротивления, величину и полярность ЭДС E и величину напряжения U, приложенного к схеме. Для проверки правильности расчета составить уравнение баланса мощностей. Определить показание вольтметра. 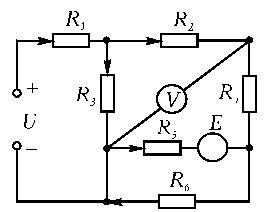 Рис.1 Рис.1Таблица 1
Задача 2. В схеме (рис.2) Е1 = 60 В, E6 = 120 В, Е11 = 90 В, R1 = 4 Ом, R2 = 65 Ом, R3 = 9 Ом, R6 = 12 Ом, R8 = 48 Ом, R9 = 5 Ом. Значения остальных сопротивлений даны в таблице 2. Начертить расчетную электрическую схему, получающуюся при замыкании ключей, указанных в таблице 2. 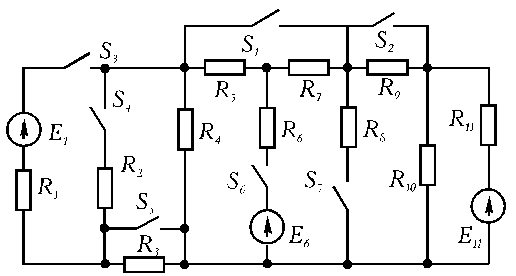 Рис.2 Таблица 2
Упростить схему, заменяя последовательно и параллельно соединенные сопротивления эквивалентными, используя при необходимости преобразование треугольника сопротивлений в эквивалентную звезду. Полученную схему с двумя узлами рассчитать методом узлового напряжения, определить величину и направление токов в источниках. Зная токи источников, используя законы Ома и Кирхгофа, определить все токи и напряжения в исходной расчетной схеме. Для проверки правильности расчета составить для исходной схемы уравнение баланса мощностей. Задача 1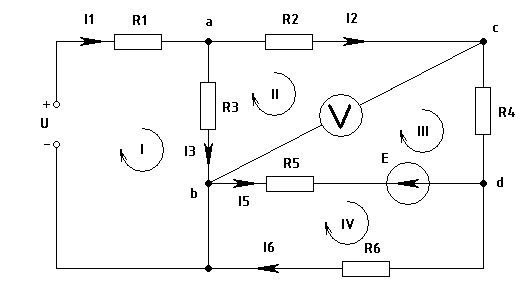 Рис. 3 Исходная схема. Дано: R1 = 2 Ом, R2 = 3 Ом, R4 = 4.5 Ом, R5 = 2 Ом, R6 = 2.7 Ом, I2 = 1.8 А, I3 = 1.5 А, I6 = 0.3 А. Найти: I1, I5, R3, U, E, Ub-c. По первому закону Кирхгофа (для узлов): для узла а: I1 = I3 + I2=> I1 = 3.3 A для узла d: I5 = I6 + I2=> I5 = - 1.5 A Вывод: так как I5 < 0 то направление тока I5 противоположно показному на схеме (рис.3) По второму закону Кирхгофа (для контуров): для контура I : U = R1*I1 + R3*I3 для контура II+III: E = - R5*I5 – R3*I3 + (R2 + R4) *I2 для контура IV: - E = R6*I6 + R5*I5=> E = 2. 19 В Из уравнений для II +III контура выразим R3: R3 = (-R5*I5 + (R2 + R4) *I2-E) / I3=> R3 = 9.54 В U = R1*I1 + R3*I3 => U = 20.91 В Рассчитаем Ub-c по второму закону Кирхгофа для контура II: Ub-c = R3*I3 – R2*I2 => Ub-c = 8.91 В Проверка результатов: по первому закону Кирхгофа для узла b: I1 = I3 - I5 + I6 = 3.3 A по второму закону Кирхгофа для контура II+III+IV: 0 = - I3*R3 + I2*(R2 + R4) + I6*R6 = 0 составим уравнение баланса мощностей: U*I1 + E*I5 = R1*I12 + (R2 + R4) *I22 + R3*I32 + R5*I52 + R6*I62 => 72.288 = 72.288 Вывод: проведённые проверки подтверждают что результаты решения задачи 1 верны. Найдено: I1 = 3.3 А, I5 = 1.5 А и протекает в противоположном показному на схеме(рис.3) направлений, R3 = 9.54 Ом, U = 20.91 В, E =2. 19 В, Ub-c=8.91 В. Задача 2 Рис.4 Исходная схема. Дано: R1 = 4 Ом, R3 = 9 Ом, R4 = 16 Ом, R5 = 28 Ом, R7 = 4 Ом, R8 = 48 Ом R10 = 24 Ом, R11 = 15 Ом, E1 = 60 B, E11 = 90 B. Объединим сопротивления: R(1,3) = R1 + R3, => R(1,3) = 13 Ом R(5,7) = R5 +R7, => R(5,7) = 32 Ом R(8,10) = (R8*R10) / (R8 + R10). => R(8,10) = 16 Ом 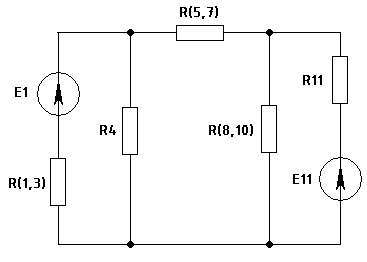 Рис.5 Схема после объединения сопротивлений. Преобразуем треугольник сопротивлений R4, R(5,7), R(8,10) в эквивалентную звезду: R(4-5,7) = (R4 * R(5,7)) / (R4 + R(5,7) + R(8,10)) => R(4-5,7) = 8 Ом R(5,7-8,10) = (R(5,7) * R(8,10)) / (R4 + R(5,7) + R(8,10)) => R(5,7-8,10) = 8Ом R(4-8,10) = (R(4) * R(8,10)) / (R4 + R(5,7) + R(8,10)) => R(4-8,10) = 4 Ом 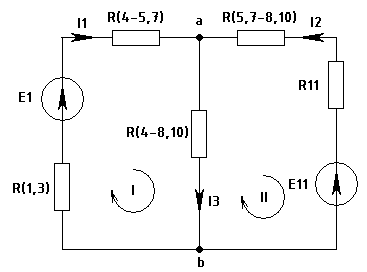 Рис. 6 Схема после преобразования треугольника в звезду По первому закону Кирхгофа: для узла а: I3 = I1 +I2 (1) По второму закону Кирхгофа: для контура I: E1 = (R(4-5,7) + R(1,3)) *I1 + R(4-8,10) *I3(2) для контура II: - E11 = - R(4-8,10) *I3 – (R(5,7-8,10) + R11) *I2(3) Запишем уравнения для Ua-b: Ua-b = R(4-8,10) *I3(4) из (2) выразим I1 = (E1 - R(4-8,10) *I3) / (R(4-5,7) + R(1,3)) (5) из (3) выразим I2 = (E11 - R(4-8,10) *I3) / (R(5,7-8,10) + R11) (6) подставим в (1) I3 = (E1 - R(4-8,10) * I3) / (R(4-5,7) + R(1,3)) + + (E11 - R(4-8,10) * I3) / (R(5,7-8,10) + R11) 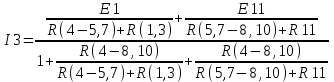 => => I3 = 4.962 A из (5) I1 = 1.912 A из (1) I2 = 3.05 A из (4) Ua-b = 19.848 В Проверка результатов: по первому закону Кирхгофа для узла b: I3 = I1 +I2 = 4.962 A по второму закону Кирхгофа для контура I+II: E1-E11=(R(4-5,7) +R(1,3)) *I1+R(4-8,10) *I3-R(4-8,10) *I3-(R(5,7-8,10) +R11) *I2 30 ≈ - 30 составим уравнение баланса мощностей: E1*I1 + E11*I2 = (R(4-5,7) +R(1,3)) *I12 + R(4-8,10) *I32 + (R(5,7-8,10) +R11) *I22 397,2 ≈ 397,2 Вывод: проведённые проверки подтверждают что результаты решения задачи 2 верны. Найдено: I1 = 1.912 А, I2 = 3.05 А, I3 = 4.962 А, Uа-b = 19.848 В. Определим остальные токи и напряжения в схеме, для этого зададимся направлениями токов в схеме.  Рис.7 Исходная схема с обозначенными токами. По первому закону Кирхгофа (для узлов): для узла с: I1= - I5 + I4(7) для узла d: I2= - I5 + I8 + I10(8) По второму закону Кирхгофа: Ue-c = E1 - R(1,3) *I1=> Ue-c = 35.144 B Ue-d = E11 - R11*I2=> Ue-d = 44.249 B По закону Ома: I4 = Ue-c / R4=> I4 = 2. 197 A I10 = Ue-d / R10=> I10 = 1.844 A I8 = Ue-d / R8=> I8 = 0.922 A из(7) I5 = 0.285 А На данном этапе мы рассчитали все токи в исходной схеме теперь по закону Ома заполним таблицу 3 Таблица 3.
Проверка результатов: составим уравнение баланса мощностей для исходной схемы E1*I1 + E11*I2=P1 + P3 + P4 + P5 + P7 + P8 + P10 + P11 397,23 ≈ 389.87 Вывод: проведённые проверки подтверждают что результаты решения задачи 2 верны. Найдено: Все найденные величины приведены в таблице 3. Рассчитаем схему (Рис.6) методом узлового напряжения. Запишем формулу для Ua-b: 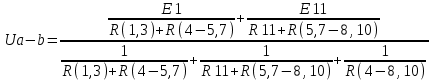 Ua-b = 19.85 В из формулы (4) выразим I3 и найдём его I3 = 4.962 A используя формулы (4) и (5) найдём I1 = 1.912 A используя формулы (4) и (6) найдём I2 = 3.05 А Вывод: результаты расчёта схемы методами узлового напряжения и по законам Кирхгофа получились идентичными что говорит о том что результат независим от метода расчётов. |
