работа по математической биостатистике. Контрольная работа по МАТЕМАТИЧЕСКОЙ БИОСТАТИСТИКЕ АВрхипова В. Контрольная работа по Математической биостатистике Вариант 1 специальность 36. 05. 01 Ветеринария
 Скачать 80.17 Kb.
|
|
ЗАДАНИЕ 2 ЗАДАНИЕ 2.1. Проверить гипотезу о равенстве двух генеральных средних с использованием критериев Стьюдента и Уилкоксона (Манна-Уитни). Сформулировать нулевую и альтернативную гипотезы. Сделать выводы на уровне значимости α=0,05 о существовании различий в средних уровнях изучаемого параметра у здорового и больного животного. Результаты измерения холестерина в крови (ммоль/л) у здоровых собак (норма) и у собак, больных гипотиреозом (заболевание щитовидной железы), представлены в таблице 2.1 Таблица 2.1 – Содержание холестерина (ммоль/л)
Решение. Нулевая гипотеза (Н0): выборки извлечены из одной и той же генеральной совокупности. Альтернативная гипотеза (Н1): выборки извлечены из разных генеральных совокупностей. Вычислим средние значения содержания холестерина в крови и показатели дисперсий по двум данным контрольным группам (выборкам), используя таблицу 2.2. Таблица 2.2 - Расчет средних значений и показателей дисперсий выборок
Средние значения содержания холестерина в крови по группам равны: 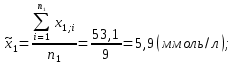 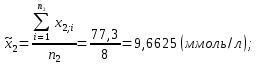 Дисперсии для групп собак составляют: 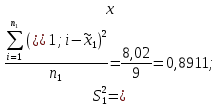 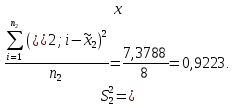 Из полученных результатов расчетов видно, что средние 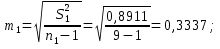 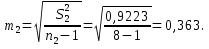. Таким образом, можно предположить, что содержание холестерина в крови в контрольных группах собак в среднем не одинаково. Проверим достоверность этого предположения с помощью критерия Стьюдента. Условие применения критерия Стьюдента выполняется, т.к. дисперсии выборок  примерно одинаковы. Вычислим значения стандартных ошибок:  Расчётное значение критерия Стьюдента: 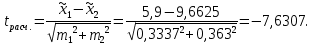 По таблице распределения Стьюдента для уровня значимости α = 0,05 и числа степеней свободы k = n1 + n2 – 2 = 9 + 8 - 2 = 15 значение критерия составляет 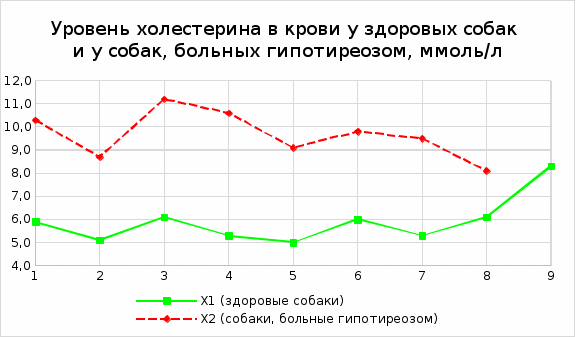  , поэтому на 5%-ном уровне значимости статистически доказано, что различия в среднем содержании холестерина в крови у здоровых и больных гипотиреозом собак существенны. Представим результаты исследования в графическом виде (рис. 2.1). Рис. 2.1 Сравнение содержания холестерина в крови у здоровых и у собак, больных гипотиреозом Используем непараметрический критерий Уилкоксона. Выполним ранжирование исходных данных и вычислим сумму рангов в каждой группе, используя таблицу 2.3. Таблица 2.3 – Расчет суммы рангов
Расчетные значения U-критерия для каждой группы:   Сравнение полученных значений критерия и анализ характера распределения значений признака по обобщенному ряду показывает, что различия между наблюдениями в группах существенны и нулевая гипотеза о том, что выборки извлечены из одной и той же генеральной совокупности, отвергается. Тестовое значение Uрасч = -1. По таблице Манна-Уитни для n1 = 9 и n2 = 8 при 5%-ном уровне значимости Uтабл не определено. Соседние значения Uтабл > Uрасч,, а значит на 5%-ном уровне значимости можно утверждать, что различия в значениях содержания холестерина в крови у здоровых собак и у собак, больных гипотиреозом, считаются достоверными и статистически значимыми. Это соответствует выводу, полученному ранее. ЗАДАНИЕ 2.2. Результаты измерения влияния микробиологического препарата «Б1-У» («Урга» - полный аналог препарата «Байкал ЭМ1») на продуктивность молочных коров по результатам опытного применения на контрольной группе 10 коров представлены в таблице 2.4. Определите, на какую величину в среднем увеличивается надой после применения препарата? Достоверны ли полученные результаты, указывающие на увеличение удойности коров вследствие применения препарата? Докажите статистическую достоверность эффективности «Б1-У». Представьте результаты в графическом виде. Таблица 2.4 – Результаты измерения влияния микробиологического препарата «Б1-У»
Решение. Нулевая гипотеза (Н0): увеличение удойности коров контрольной группы в результате использования препарата «Б1-У» равно нулю. Альтернативная гипотеза (Н1): увеличение удойности коров контрольной группы в результате использования препарата «Б1-У» не равно нулю. Для наглядности представим расчетные данные в таблице 2.5. Таблица 2.5 – Расчет средних значений и попарных разностей результатов удойности коров
Среднее значение попарных разностей составляет: 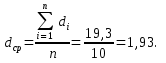 Таким образом, в среднем надой увеличивается на 1,93 л/сутки после применения препарата. Показатель дисперсии значений попарных разностей равен: 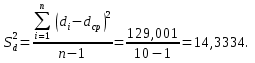 Вычислим стандартную ошибку среднего значения попарных разностей:  Расчетное значение критерия Стьюдента:  По таблице распределения Стьюдента для уровня значимости α = 0,05 и числа степеней свободы k = n – 1 = 10 - 1 = 9 значение критерия составляет   , поэтому на 5%-ном уровне значимости различия между средними значениями удойности до и после использования препарата принимаются несущественными. Таким образом, эффективность использования препарата «Б1-У» статистически не доказана.Представим результаты исследования в графическом виде (рис 2.2). 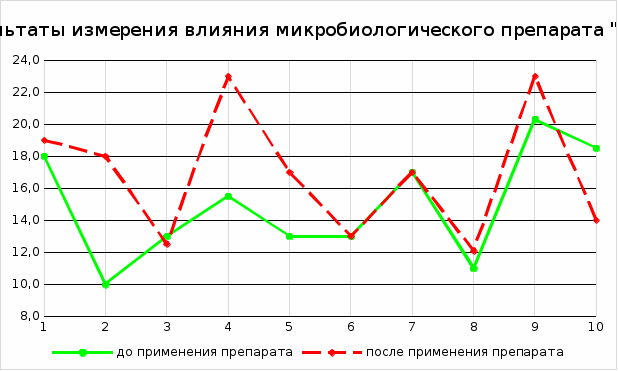 Рис. 2.2 Сравнение результатов удойности коров |
(количественная разность)