аа. Контр_работа N2_2016. Контрольная работа по общей физике 2
 Скачать 3.84 Mb. Скачать 3.84 Mb.
|
ЗАДАЧИ1.1.Температура 1.2.Температура 1.3.Вследствие изменения температуры абсолютно черного тела максимум спектральной плотности излучения сместился с 2.4 мкм на 0.8 мкм. Как и во сколько раз изменилась энергетическая светимость и максимальная спектральная плотность излучательной способности. Построить графики спектральной плотности излучательной способности при этих температурах. 1.4.Абсолютно черное тело имеет температуру 500 К. Какова будет температура тела, если в результате нагревания поток излучения увеличится в 5 раз? Исходя из формулы Планка, изобразить графически начальный и конечный спектры излучения. 1.5. Как и во сколько изменится поток излучения абсолютно черного тела, если максимум видимого света излучения переместится с красной границы спектра 780 нм на фиолетовую 390 нм? Построить графики спектральной плотности излучательной способности при этих температурах. 1.6. Интенсивность солнечного излучения вблизи Земли за пределами её атмосферы равна 1350 Дж/м2с. Принимая, что Солнце излучает как абсолютно черное тело, определить температуру его излучающей поверхности. Радиус Солнца равен 1.7. Определить температуру и энергетическую светимость абсолютно черного тела, если максимум энергии спектра излучения приходится на длину волны 600 нм. Построить график спектральной плотности излучательной способности при этой температуре. 1.8. Температура абсолютно черного тела равна 2000 К. Определить длину волны 1.9. При остывании абсолютно черного тела максимум его спектра излучения сместился на 500 нм. На сколько градусов остыло тела. Начальная температура тела 2500 К. Построить графики спектральной плотности излучательной способности при этих температурах. 1.10. Абсолютно черное тело имеет температуру Фотоэффект 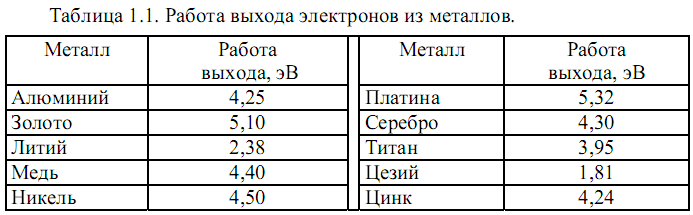 2.1. При поочередном освещении поверхности некоторого металла светом с длинами волн 2.2.Определить максимальную скорость 2.3. Красная граница фотоэффекта для цинка составляет 310 нм. Определить максимальную кинетическую энергию (в электрон-вольтах) фотоэлектронов и задерживающую разность потенциалов, если на цинк падает ультрафиолетовое излучение с длиной волны 200 нм. 2.4. На поверхность калия падает ультрафиолетовое излучение с длиной волны 150 нм. Определить максимальную кинетическую энергию фотоэлектронов (в электрон-вольтах) и задерживающую разность потенциалов. 2.5. Фотон с энергией 10 эВ выбивает электроны из серебряной пластины. Определить импульс, полученный пластиной, если принять во внимание, что направления импульсов фотона и фотоэлектрона перпендикулярны плоскости пластины. 2.6. На фотоэлемент с катодом из лития падает ультрафиолетовое излучение с длиной волны 200 нм. Найти наименьшее значение задерживающей разности потенциалов, прекращающее фототок. 2.7. Какова должна быть длина волны излучения, падающего на платиновую пластину, если максимальная скорость фотоэлектронов равна 2.8. Ультрафиолетовое излучение с длиной волны 0.25 мкм, направленное на металлическую пластину, вызывает фототок, который прекращается при минимальной задерживающей разности потенциалов 0.96 В. Определить работу выхода электрона из металла. 2.9. На поверхность металла падает ультрафиолетовое излучение с длиной волны 0.1 мкм. Красная граница фотоэффекта равна 0.3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии? 2.10. На поверхность лития падает рентгеновское излучение с длиной волны 1 нм. Определить максимальную скорость фотоэлектронов. Можно ли пренебречь работой выхода электрона? 3. Квантовые ямы 3.1. Электрон находится внутри одномерной прямоугольной потенциальной ямы с абсолютно непроницаемыми стенками. Ширина ямы 0.2 нм, энергия электрона 37.8 эВ. Определить номер энергетического уровня и значение волнового вектора 3.2 Вычислить отношение вероятностей нахождения электрона на первом и втором энергетических уровнях в интервале протяженностью в четверть ширины квантовой ямы и равноудаленной от стенок одномерной потенциальной ямы с абсолютно непроницаемыми стенками. шириной 0.20 нм. 3.3. Волновая функция гармонического осциллятора, находящаяся в основном состоянии, имеет вид 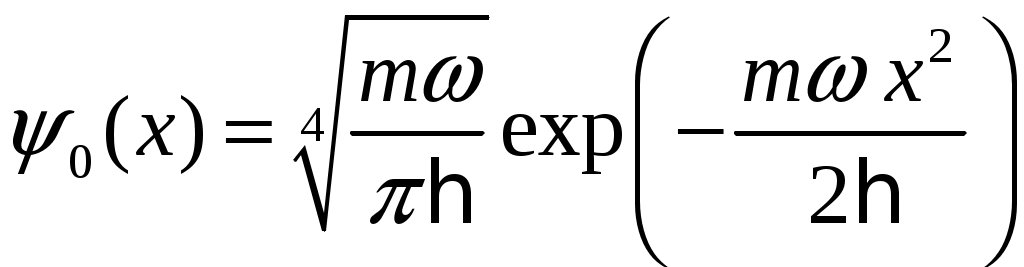 . . Найти вероятность обнаружения частицы вне пределов классической области, в которой кинетическая энергия 3.4. Электрон находится в одномерном потенциальном ящике с бесконечно высокими стенками в состоянии, характеризуемом квантовым числом 3.5. Электрон находится в одномерной прямоугольной квантовой яме шириной 3.6. Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти ширину ямы, если разность энергий между вторым и третьим энергетическим уровнями составляет 0.3 эВ. 3.7. Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна 3.8. Электрон находится в потенциальном ящике шириной 3.9. Изобразить на графике вид первых трех собственных стационарных волновых функций 3.10. Частица в потенциальном ящике шириной 4. Туннелирование Пример 4.1. Определить вероятность отражения электрона при рассеянии его квантовой ямой глубиной в 1 эВ и шириной в 1 нм. Энергия падающего электрона равна 0.25 эВ. Построить график зависимости вероятности отражения электрона от его энергии. Н 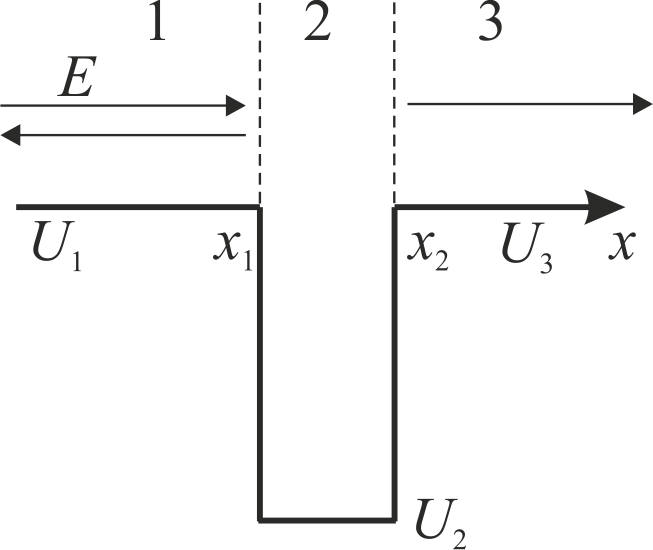 а рис. 4.1 представлена координатно-энергетическая диаграмма квантовой структуры: а рис. 4.1 представлена координатно-энергетическая диаграмма квантовой структуры: Математическая модель 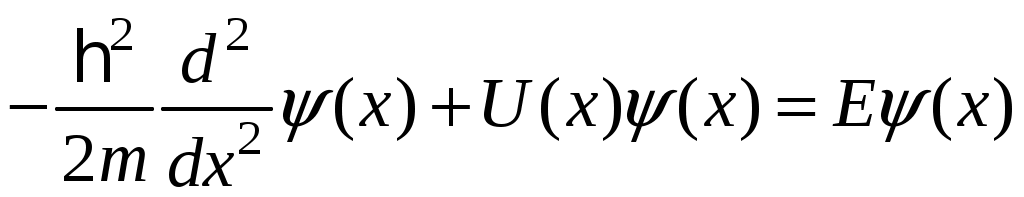 (1) (1)Условие непрерывности на границах раздела слоев квантовой гетероструктуры, приведенной на рис. 4.1. 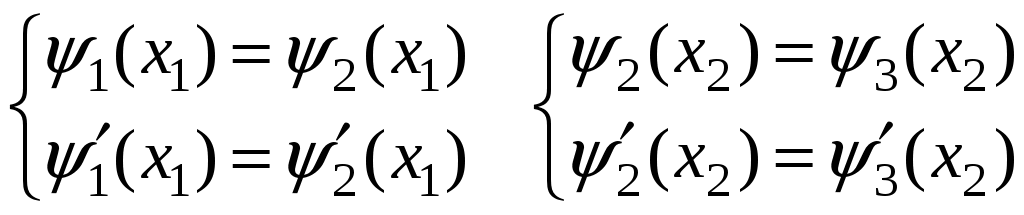 (2) (2)Решение (1) удобно представить в виде прямых и обратных плоских волн где 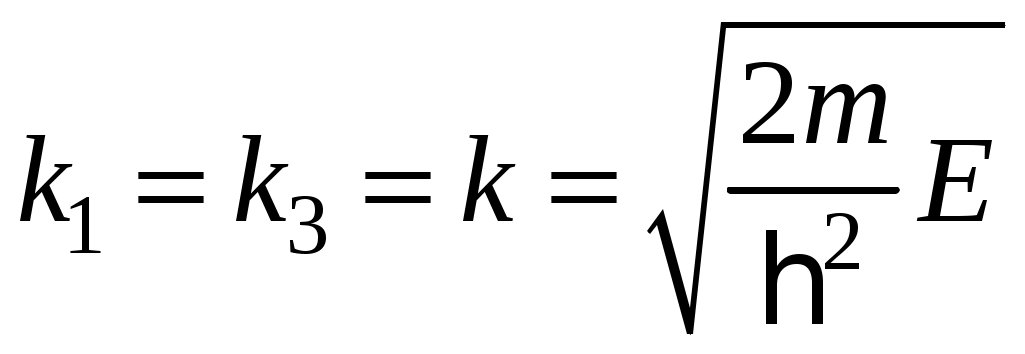 (6) (6)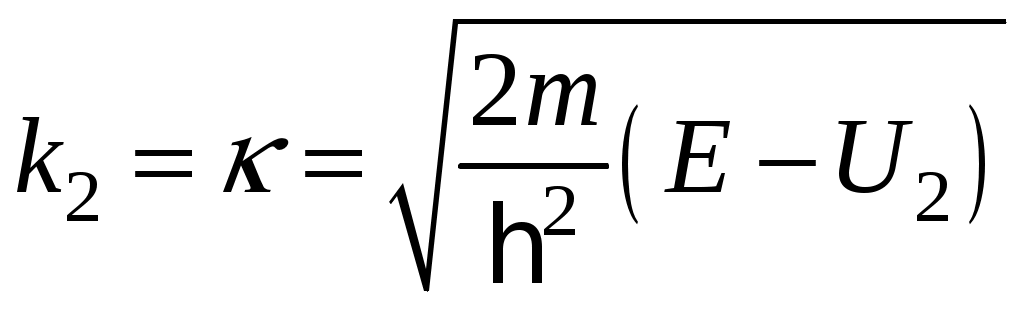 (7) (7)Граничные условия такие Требуется найти вероятность 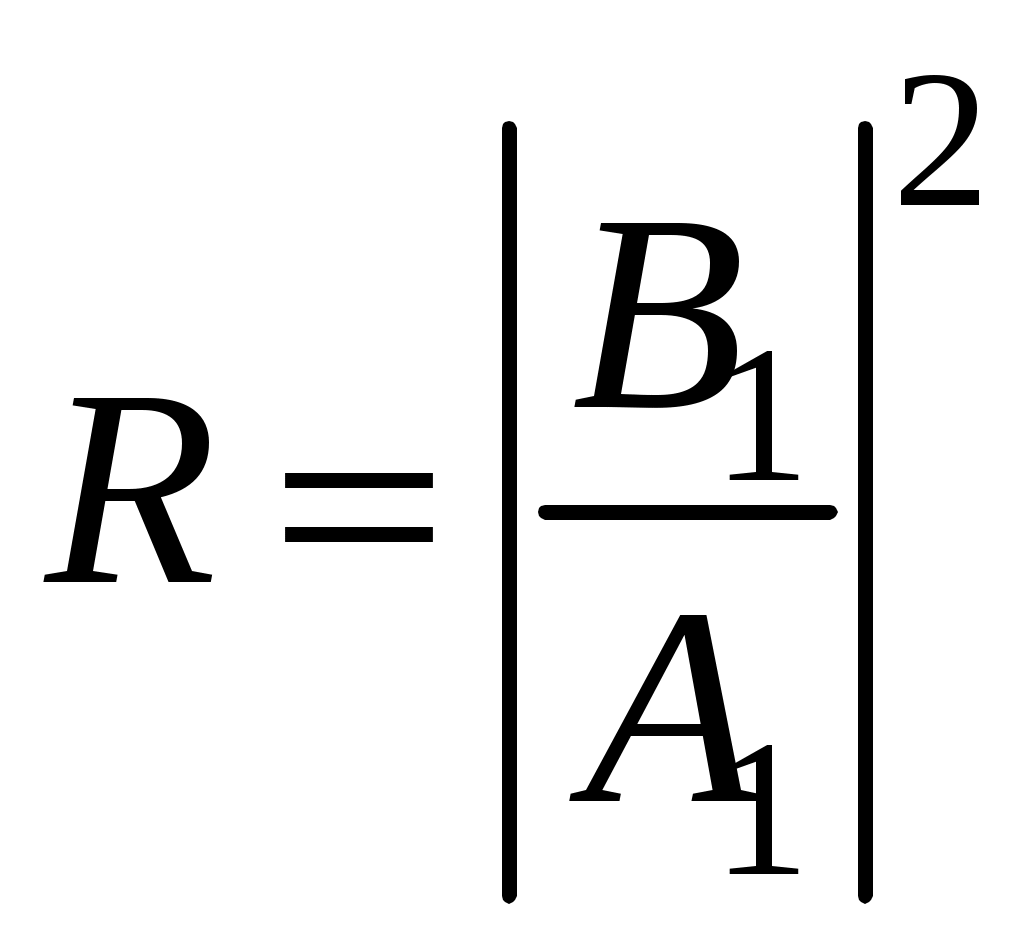 (10) (10)Решение Удобно условия (2) представить в матричном виде 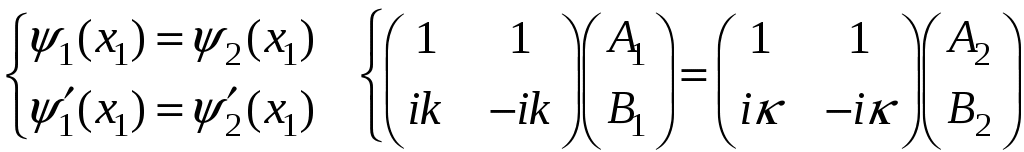 (11) (11)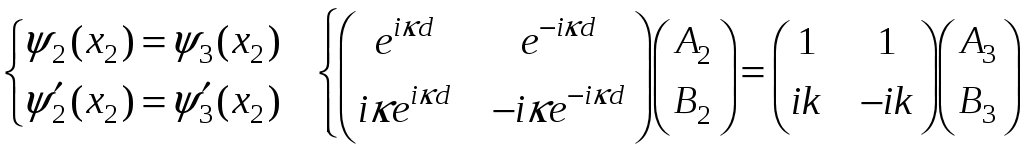 (12) (12)Наша задача найти амплитуды 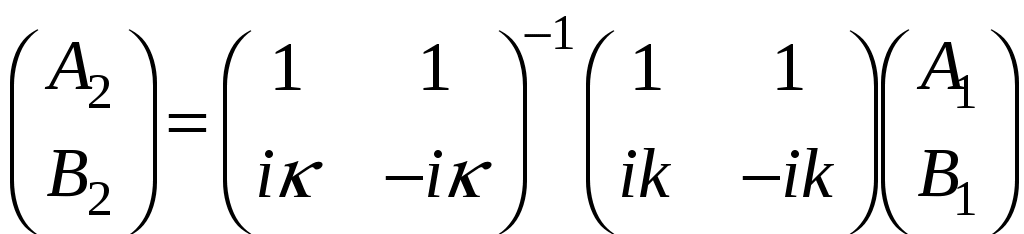 , (13) , (13)а из (12) выразим амплитуды третьего слоя через амплитуды первого слоя 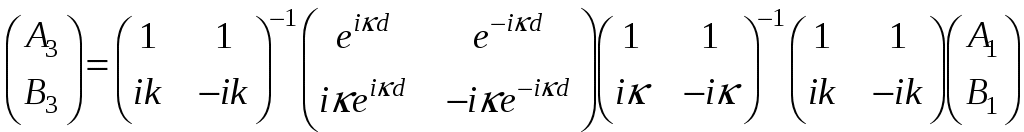 (14) (14)В сокращенной форме (14) запишется в виде 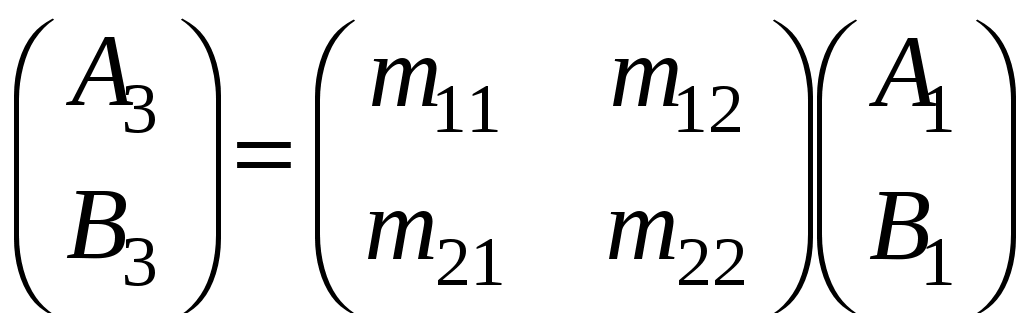 или или 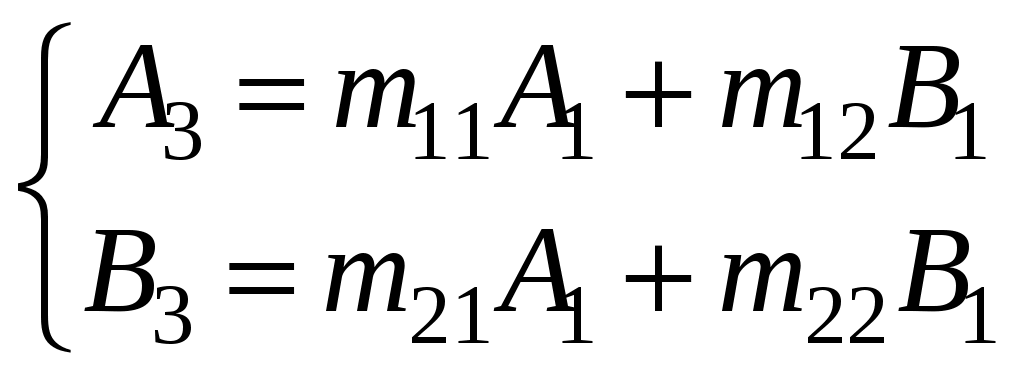 (15) (15)С учетом граничного условия (9) запишем 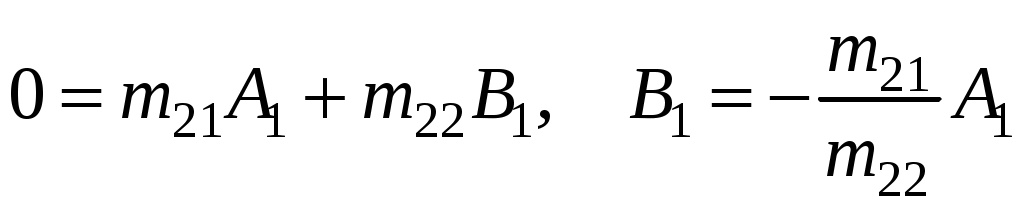 (16) (16)И, окончательно, вероятность отражения электрона квантовой ямой есть 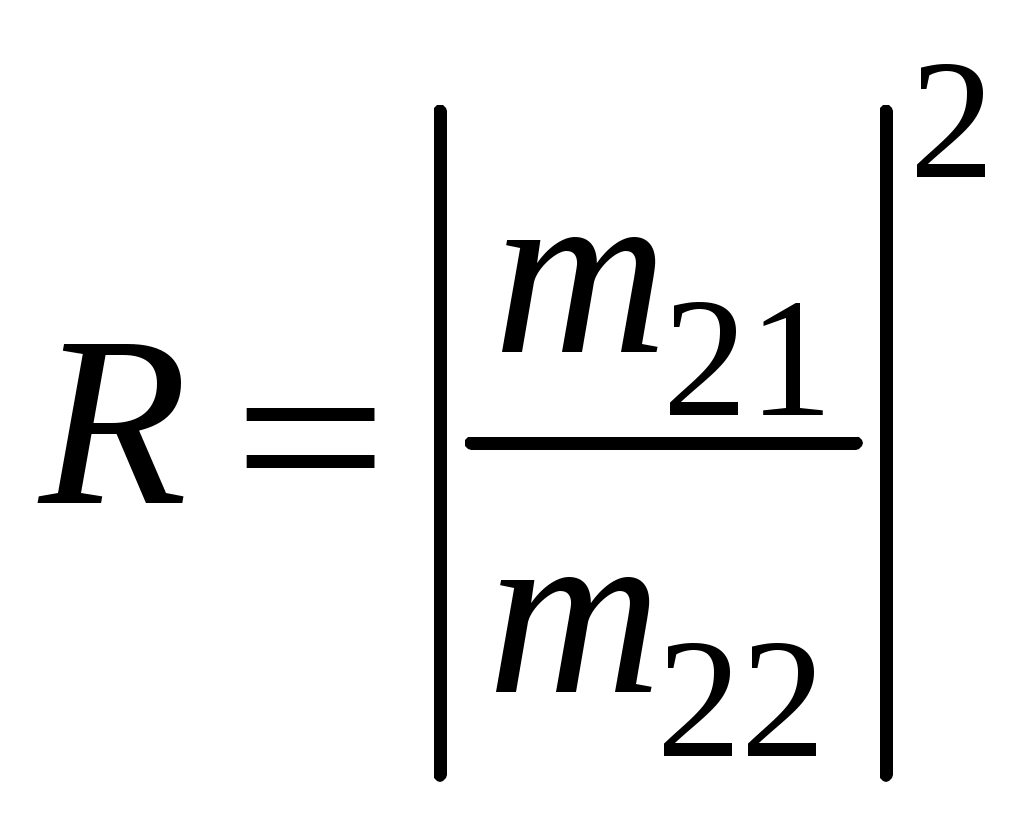 (17) (17)Предоставим умножение матриц в (14) вычислительной технике, запишем простейший код в maple > > > > 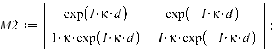 > 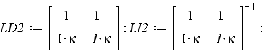 > > Построим требуемый график 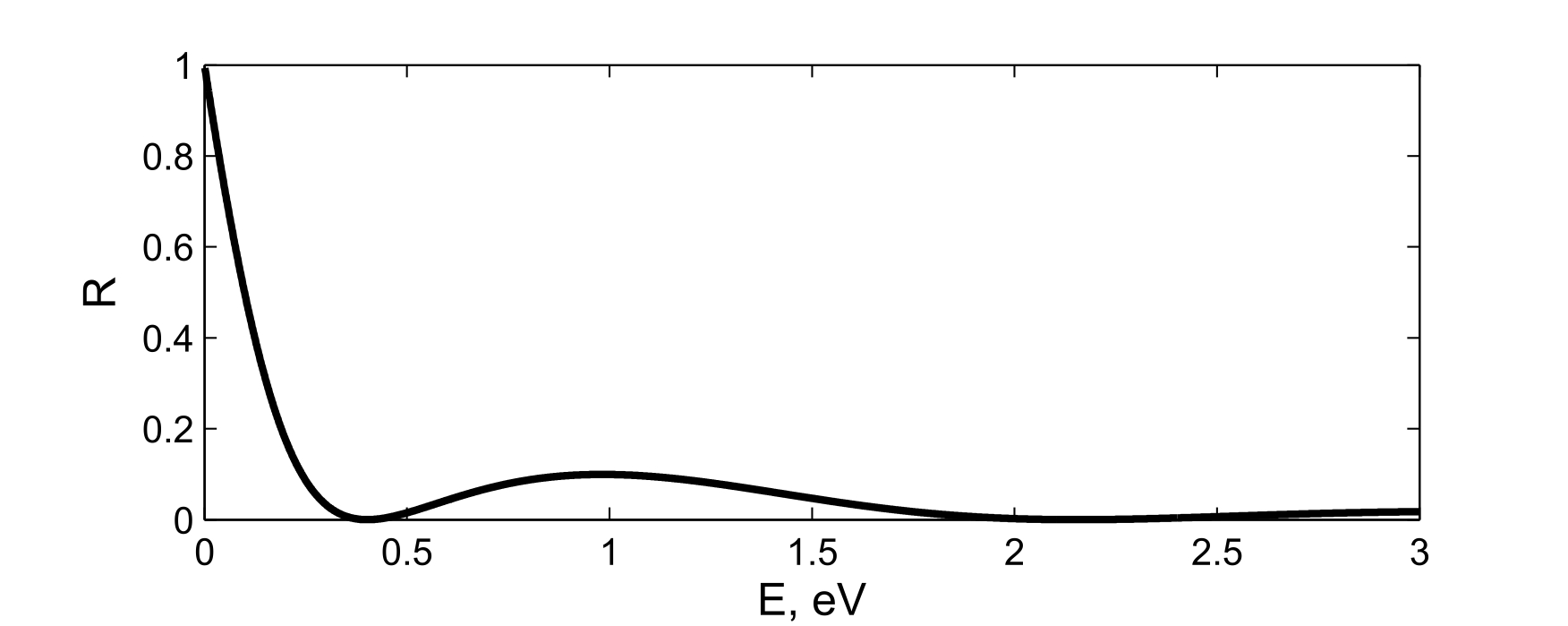 Рис.4.2 Вероятность отражения электрона от квантовой ямы в зависимости от энергии электрона. Как видно из рис.4.2 за исключением отдельных значений энергии электрон отражается квантовой ямой, это квантовый эффект, так как классическая частица не отражается потенциальной ямой, но изменяет свою скорость в области изменения потенциальной энергии. 4.1. Электрон обладает энергией 10 эВ. Определить, во сколько раз изменится его скорость 4.2. Протон с энергией 4.3. На пути электронов с длиной волны де Бройля 4.4. Электрон с энергией 100 эВ падает на бесконечно широкий потенциальный барьер высотой 64 эВ. Определить вероятность 4.5.Коэффициент отражения 4.6 Электрон с энергией 4.7. Электрон проходит через прямоугольный потенциальный барьер шириной 4.8. Найти вероятность 4.9 Протон и электрон прошли одинаковую ускоряющую разность потенциалов 4.10. Электрон с энергией 5. Атомы и молекулы 5.1. Электрон в возбужденном атоме водорода находится в 3p-состоянии. Определите изменение магнитного момента, обусловленного орбитальным движением электрона, при переходе атома в основное состояние 5.2. Электрон в невозбужденном атоме водорода получил энергию 12,1 эВ. На какой энергетический уровень он перешел? Сколько линий спектра могут излучиться при переходе электрона на более низкие энергетические уровни? Вычислите соответствующие длины волн. 5.3. Максимальная длина волны спектральной водородной линии серии Лаймана равна 0.12 мкм. Предполагая, что постоянная Ридберга неизвестна, определите максимальную длину волны линии серии Бальмера. 5.4. Атом водорода, находившийся первоначально в основном состоянии, поглотил квант света с энергией 5.5. Момент импульса 5.6. Электрон в возбужденном атоме водорода находится в 5.7. В эксперименте измерены энергии перехода между тремя последовательными уровнями энергии вращательной полосы двухатомной молекулы. Найдите квантовые числа J этих уровней и момент инерции I молекулы. 5.8. Определите для молекулы 5.9. Для молекулы 5.10. Покажите, что интервалы частот между соседними спектральными линиями чисто вращательного спектра двухатомной молекулы имеют одинаковую величину. Найдите расстояние между ядрами молекулы |
