теория игр контрольная. теория_игр_решение_9вар. Контрольная работа по предмету теория игр

• Название: Контрольная работа по предмету теория игр
• Анкор: теория игр контрольная
• Дата: 20.07.2022
• Размер: 146.09 Kb.
• Имя файла: теория_игр_решение_9вар.docx
• Тип: Контрольная работа; #633937
• страница: 4 из 4

ЗАДАНИЕ 4

Нефтяная компания собирается построить в районе крайнего севера нефтяную вышку. Имеется 4 проекта A, B, C и D. Затраты на строительство (млн. руб.) зависят от того, какие погодные условия будут в период строительства. Возможны четыре варианта погоды S₁, S₂, S₃ и S₄.

Используя критерии Вальда, максимального оптимизма, Гурвица (при α=0,6), Сэвиджа и Лапласа, выбрать оптимальный проект для строительства. Матрица затрат имеет вид: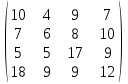


Решение:

По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е. W = max(min a_ij)

Критерий основывается на том, что, если состояние обстановки неизвестно, нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффективности каждой системы.

Для применения критерия нужно для каждой альтернативы выбрать наихудший показатель привлекательности (наименьшее число в каждой строке матрицы выигрышей) и выбрать ту альтернативу, для которой этот показатель максимальный.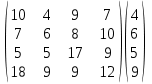



В каждой строке матрицы эффективности находится минимальная из оценок систем по различным состояниям обстановки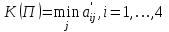

K(A) = 4 K(B) = 6 K(C) = 5 K(D) = 9

Оптимальной считается система из строки с максимальным значением эффективности: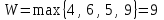



Лучший проект по критерию Вальда – D.

Критерий максимального оптимизма – наиболее простой критерий, основывающийся на идее, что игрок, имея возможность в некоторой степени управлять ситуацией, рассчитывает, что произойдет такое развитие ситуации, которое для него является наиболее выгодным. В соответствии с критерием принимается альтернатива, соответствующая максимальному элементу матрицы выигрышей или минимальному элементу матрицы затрат.

Для применения критерия нужно для каждой альтернативы выбрать наилучший показатель привлекательности (наибольшее число в каждой строке матрицы выигрышей) и выбрать ту альтернативу, для которой этот показатель максимальный.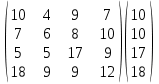



Для рассматриваемой задачи эта величина a₄₁=18, поэтому лучшая стратегия по критерию максимального оптимизма – D.

Критерий Гурвица является критерием пессимизма-оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение:

max(s_i), где s_i = min(a_ij) + (1–)max(a_ij)

По условию, =0,6.

Рассчитываем s_i.

s₁ = 0,64+(1–0,6)10 = 6,4 s₂ = 0,66+(1–0,6)10 = 7,6

s₃ = 0,65+(1–0,6)17 = 9,8 s₄ = 0,69+(1–0,6)18 = 12,6

	S1	S2	S3	S4	min(a’ij)	max(a’ij)	min(a’ij) + (1–)max(a’ij)
A	10	4	9	7	4	10	6,4
B	7	6	8	10	6	10	7,6
C	5	5	17	9	5	17	9,8
D	18	11	9	12	9	18	12,6

Выбираем из (6,4; 7,6; 9,8; 12,6) максимальный элемент: max=12,6

Вывод: выбираем проект D.
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:

a = min(max r_ij)

Элементы матрицы риска находятся по формуле: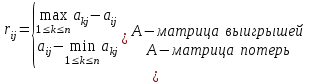



Находим матрицу рисков.

1. Рассчитываем 1-й столбец матрицы рисков.

r₁₁ = 18 – 10 = 8; r₂₁ = 18 – 7 = 11; r₃₁ = 18 – 5 = 13; r₄₁ = 18 – 18 = 0;

2. Рассчитываем 2-й столбец матрицы рисков.

r₁₂ = 11 – 4 = 7; r₂₂ = 11 – 6 = 5; r₃₂ = 11 – 5 = 6; r₄₂ = 11 – 11 = 0;

3. Рассчитываем 3-й столбец матрицы рисков.

r₁₃ = 17 – 9 = 8; r₂₃ = 17 – 8 = 9; r₃₃ = 17 – 17 = 0; r₄₃ = 17 – 9 = 8;

4. Рассчитываем 4-й столбец матрицы рисков.

r₁₄ = 12 – 7 = 8; r₂₄ = 12 – 10 = 3; r₃₄ = 12 – 8 = 4; r₄₄ = 12 – 12 = 0.
Результаты вычислений оформим в виде таблицы.

	S1	S2	S3	S4	max(rij)
A	8	7	8	5	8
B	11	5	9	2	11
C	13	6	0	4	13
D	0	0	8	0	8

Выбираем из (8; 11; 13; 8) минимальный элемент: min=8

Вывод: выбираем проект D.
Критерий Лапласа основан на предположении, что каждый вариант развития ситуации (состояния «природы») равновероятен. Поэтому, для принятия решения, необходимо рассчитать функцию полезности для каждой альтернативы, равную среднеарифметическому показателей привлекательности по каждому «состоянию природы»: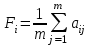



Выбирается та альтернатива, для которой функция полезности максимальна.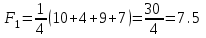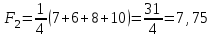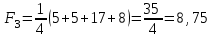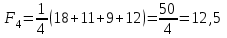









Выбираем из (7,5; 7,75; 8,75; 12,5) максимальный элемент: max=12,5.

Вывод: выбираем проект D.
Таким образом, в результате решения статистической игры рекомендуется проект D, как наиболее удачный по всем критериям.
Ответ: наиболее удачен проект D.