теория игр контрольная. теория_игр_решение_9вар. Контрольная работа по предмету теория игр
 Скачать 146.09 Kb. Скачать 146.09 Kb.
|
|
ЗАДАНИЕ 2 Предприниматель А планирует начать выпуск изделий Т1 и Т2. Ожидаемая прибыль зависит от того, какой вид изделий Т1 или Т2 будет выпускать конкурент. Если оба будут производить изделия Т1, то ввиду конкуренции А понесёт убытки в X тыс. руб. Если оба будут производить Т2, то по той же причине А понесёт убытки в Y тыс. руб. Если А будет производить Т1, а В – Т2, то прибыль А составит Z тыс. руб. Если А будет производить Т2, а В – Т1, то прибыль А составит T тыс. руб. Найти оптимальные стратегии каждого из предпринимателей. X=100, Y=350, Z=900, T=600 Решение: Платежная матрица игры имеет вид: 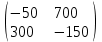 Найдем нижнюю и верхнюю цену игры. В каждой строке платежной матрицы найдем наименьший элемент, и запишем его справа от матрицы. В каждом столбце платежной матрицы найдем наибольший элемент, и запишем его снизу от матрицы. В результате получим таблицу
Нижняя цена игры max{50,150} 50. Верхняя цена игры min{300,700} 300. Так как нижняя и верхняя цены игры не совпадают, то рассмотренная игра не имеет седловой точки. В этом случае решение нужно искать в области смешанных стратегий. У игрока A в рассматриваемой задаче есть две чистые стратегии: A1 и A2. Смешанная стратегия игрока A состоит в том, чтобы применять эти чистые стратегии, чередуя их по случайному закону с частотами p1 и p2, причем p1 + p2=1. Смешанную стратегию игрока A обозначим через 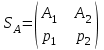 , смешанную стратегию игрока B обозначим через , смешанную стратегию игрока B обозначим через 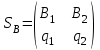 . .Средний выигрыш V при применении обоими игроками оптимальных стратегий называется ценой игры. Значения p1, p2, V, q1 и q2 определяются выражениями  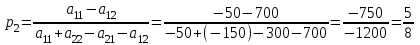 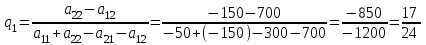  Цена игры: 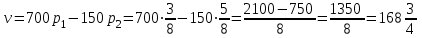 Оптимальная смешанная стратегия игрока I: 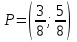 Оптимальная смешанная стратегия игрока II: 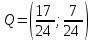 Таким образом, предпринимателю A выгодно реализовать обе стратегии A1 и A2 , чередуя выпуск изделий Т1 и Т2 по случайному закону с частотами 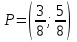 Гарантированная прибыль при этом составит 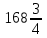 тыс. руб. тыс. руб.Предпринимателю B выгодно реализовать свои стратегии B1 и B2 с частотами 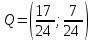 Ответ: Оптимальные стратегии предпринимателей: А – 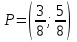 , B – , B – 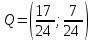 , гарантированная прибыль , гарантированная прибыль 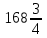 тыс. руб. тыс. руб.ЗАДАНИЕ 3 Найти решение матричной игры, сведя ее к задаче линейного программирования. 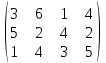 Решение: Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях. Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I. Найдем нижнюю и верхнюю цену игры. В каждой строке платежной матрицы найдем наименьший элемент, и запишем его справа от матрицы. В каждом столбце платежной матрицы найдем наибольший элемент, и запишем его снизу от матрицы. В результате получим таблицу
Нижняя цена игры max{1, 2, 1} = 2. Верхняя цена игры min{5, 6, 4, 5} 4. Так как нижняя и верхняя цены игры не совпадают, то рассмотренная игра не имеет седловой точки, цена игры находится в пределах 2 ≤ y ≤ 4. В этом случае решение нужно искать в области смешанных стратегий. Проверим платежную матрицу на доминирующие строки и доминирующие столбцы. Если в платежной матрице игры все элементы некоторой строки, определяющей стратегию Аi игрока А, не больше (меньше или некоторые равны) соответствующих элементов другой строки, то стратегия Аi называется доминируемой (заведомо невыгодной). Если в платежной матрице игры все элементы некоторого столбца, определяющего стратегию Вi игрока В не меньше (больше или некоторые равны) соответствующих элементов другого столбца, то стратегия Вi называется доминируемой (заведомо невыгодной). Решение матричной игры не изменится, если из платежной матрицы исключить строки и столбцы, соответствующие доминируемым стратегиям. Доминирующих строк и доминирующих столбцов матрица не имеет. Находим решение игры в смешанных стратегиях. Математические модели пары двойственных задач линейного программирования можно записать так: найти минимум функции F(x) при ограничениях (для игрока II): F(x) = x1+x2+x3 → min 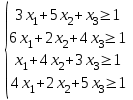 найти максимум функции Z(y) при ограничениях (для игрока I): Z(y) = y1+y2+y3+y4 → max 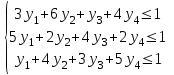 Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой функции Z(y) = y1+y2+y3+y4 при следующих ограничениях: 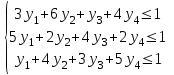 Для построения первого опорного плана приведем задачу линейного программирования к канонической форме. 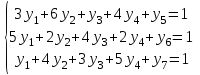 Решим систему уравнений относительно базисных переменных: y4, y5, y6. Полагая, что свободные переменные равны 0, получим первый опорный план: Y0 = (0,0,0,0,1,1,1). Составим симплекс-таблицу:
Значение целевой функции в данной точке: F= 10 + 10 + 10 + 10 + 01 + 01 + 01 = 0 Данный опорный план не является оптимальным, так как в пересечении строки 4 и столбцов y1, y2, y3, y4, y5, y6 есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-1), следовательно, в качестве ведущего выберем столбец, соответствующий переменной y4.
Вычислим значения Di по строкам как частное от деления: bi / ai4 и из них выберем наименьшее: min (1/4, 1/2, 1/5) = 1/5 Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (5) и находится на пересечении ведущего столбца и ведущей строки. Вместо переменной y7 в план 1 войдет переменная y4. Получаем новую симплекс-таблицу:
|
