КР_Виноградова Е.В._Вариант 9. Контрольная работа по программе Современные подходы к обработке и представлению результатов измерений через неопределённость в научных исследованиях, производственном контроле и метрологической деятельности Тема работы
 Скачать 68.99 Kb. Скачать 68.99 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Орловский государственный университет имени И.С. Тургенева» Центр непрерывного профессионального образования и повышения квалификации Контрольная работа по программе «Современные подходы к обработке и представлению результатов измерений через неопределённость в научных исследованиях, производственном контроле и метрологической деятельности» Тема работы: «Обработка и представление результатов измерений через неопределенность» Вариант №_9__ Слушатель: _Виноградова Е.В.  Подпись слушателя ________________ Руководитель: Подмастерьев К.В. Подпись руководителя _______________________ г. Орел, 2022 г. Условие задачи, исходные данные. При однократном измерении физической величины получено показание средства измерения X = 10. Определить, чему равно значение измеряемой величины, если экспериментатор обладает априорной информацией о средстве измерений и условиях выполнения измерений: Составление спецификации измерений Нормальный закон распределения; Значение оценки среднего квадратического отклонения: Sx = 0,1; Доверительная вероятность: P = 0,95; Значение мультипликативной (м) поправки: Qм = 1,1; Значение неисключенной систематической погрешности: Δнсп=±0,1; Цена деления: с=0,5. Решение: Расчёт неопределённости проводим в соответствии с ГОСТ 34100.3-2017 «Неопределённость измерения. Руководство по выражению неопределённости измерения». 1. Выявление и анализ факторов, влияющих на результат измерения, составление модельного уравнения. Анализ спецификации измерений позволяет определить, что на значение измеряемой величины Y наряду с показанием прибора X оказывают влияние следующие факторы: Y – значение измеряемой величины; X – показание средства измерения; Δх – основная погрешность измерения, определяемая, информацией о законе распределения результата измерений и значения среднего квадратического отклонения S; м – мультипликативная поправка; Δнсп – неисключенная систематическая погрешность; Δд – погрешность от дискретности отсчёта (определяется по цене деления шкалы средства измерения). С учётом исходных данных задачи модельное уравнение может быть представлено в следующем виде: Y = (X + Δх + Δнсп+ Δд)м. (1) 2. Оценка значений входных величин Значение входной величины X равно x= 10, поскольку X – это единственный отсчет по прибору. Значение X определяем, как середину интервала, в пределах которого находится основная погрешность прибора. Согласно информации о нормальном законе распределения и значении среднего квадратического отклонения, определяем пределы допускаемой абсолютной погрешности прибора, как 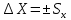 Следовательно, значение X равняется 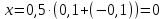 . .Значение входной величины м равно м = 1,1, поскольку это известная постоянная величина Значение величины Δнсп , заданной интервалом с пределами ±0,1 равно середине интервала, т.е. 0. Значение величины Δд определяется, как середина интервала погрешности от дискретности отсчёта. Данная погрешность определяется как ± половина цены деления: ±0,5 с = ±0,5·0,5 = ±0,25. Поэтому значение Δд также равно 0. 3. Оценка значения выходной величины Подставив значения входных величин в выражение (1), получим значение выходной величины: y = (10 + 0 + 0 + 0 )1,1 = 11. 4. Оценка стандартных неопределенностей входных величин Стандартные неопределенности величин X и м равны 0, поскольку это фиксированные величины: u(X) =0; u(м) = 0. Стандартная неопределенность основной погрешности, определяется как неопределенность по типу В. Поскольку есть информация о нормальном законе распределения и известно значение среднего квадратического отклонения, тогда: 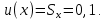 Стандартная неопределенность неисключенной систематической погрешности также определяется как неопределенность по типу В. Поскольку есть информация о нормальном законе распределения, тогда: u(Δнсп) = Δнсп = 0,1. Стандартная неопределенность от дискретности отсчета определятся аналогично: u(Δд) = Δд =0,25 Вычисление коэффициентов чувствительности и вкладов неопределенности входных величин в неопределенность результата измерений Y = (X + Δх + Δнсп+ Δд)м. Значения коэффициентов чувствительности определяются в общем случае, как: Сi = дY/дXi . Значения чувствительности равны: Сx = дY/д∆x Снсп = дY/д∆нсп Сд = дY/д∆д Сx = м = 1,1 Снсп = м= 1,1 Сд = м= 1,1 Оценка суммарной стандартной неопределенности результата измерения Принимая входные величины уравнения измерения в качестве независимых величин, суммарную стандартную неопределенность результата измерения определяем из уравнения: 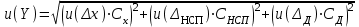 , (2) , (2)Подставив значения величин в выражение (2), получим: 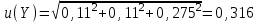 7. Определение расширенной неопределенности Расширенная неопределённость будет равна: U(y) = k· u(p) = 1,96 · 0,316 = 0,619 (3) k = 1,96 соответствует уровню доверия 95 % для нормального закона распределения. 8. Определение интервала охвата и запись результата измерения с учетом неопределенности Округляем полученные значения по правилам округления результатов измерений и получаем окончательное значение интервала неопределенности. Измеренное значение равно Ризм = (11,0 ±0,6),где число, стоящее после знака «±» – расширенная неопределенность U(y) = k · u(y),полученная длясуммарной стандартнойнеопределенности u(y) = 0,3 и коэффициента охватаk = 1,96,соответствующего уровню доверия 95 % для нормального закона распределения. 9. Бюджет неопределенности Результаты, полученные для данного примера при выполнении предшествующих этапов алгоритма, внесены в бюджет неопределенности, представленный в форме таблицы.
|