контрольные работы по геометрии 11 класс. Контрольная работа по теме Цилиндр, конус и шар
 Скачать 46.09 Kb. Скачать 46.09 Kb.
|
|
Контрольная работа по теме «Цилиндр, конус и шар» Основная цель контрольной работы: выявить уровень усвоения и прочность знаний по теме «Цилиндр, конус и шар». Вариант 1 •1. Радиус основания цилиндра равен 5 см, а высота цилиндра равна 6 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее. •2. Радиус основания конуса равен 3 м, а высота 4 м. Найдите образующую и площадь осевого сечения. 3. Радиус шара равен 17 см. Найдите площадь сечения шара, удаленного от его центра на 15 см. Контрольная работа по теме «Цилиндр, конус и шар» Вариант 2 •1. Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси цилиндра. •2. Образующая конуса l наклонена к плоскости основания под углом в 300. Найдите высоту конуса и площадь осевого сечения. 3. Радиус сферы равен 15 см. Найдите длину окружности сечения, удаленного от центра сферы на 12 см. Контрольная работа по теме «Цилиндр, конус и шар» Вариант 3 • 1. Осевое сечение цилиндра – квадрат, длина диагонали которого 36 см. Найдите радиус основания цилиндра, площадь основания цилиндра. • 2. Высота конуса равна 15 см, радиус основания 8 см. Найдите образующую конуса. 3. Шар радиусом 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найдите площадь сечения шара. Контрольная работа по теме «Цилиндр, конус и шар» Вариант 4 • 1. Осевое сечение цилиндра – квадрат, длина диагонали которого 18 см. Найдите радиус основания цилиндра, площадь основания цилиндра. • 2. Высота конуса равна 6 см, радиус основания 8 см. Найдите образующую конуса. 3. Шар радиусом 13 дм пересечен плоскостью, находящейся на расстоянии 5 дм от центра. Найдите площадь сечения шара. Контрольная работа «Объемы тел» Основная цель контрольной работы: выявить уровень усвоения и прочность знаний по теме «Объемы тел» Вариант 1 •1. Образующая конуса равна 60 см, высота 30 см. Найдите объём конуса. •2. Основание прямой призмы – прямоугольный треугольник с катетом 6 см и острым углом 450. Объем призмы равен 108 см3. Найдите площадь полной поверхности призмы. 3. Осевым сечением цилиндра является квадрат, диагональ которого равна 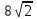 см. Найдите объем цилиндра. см. Найдите объем цилиндра.Контрольная работа «Объемы тел» Вариант 2 •1. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 300. Найдите объём конуса. •2. Основанием прямой призмы является ромб со стороной 12 см и углом 600. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы. 3. Осевым сечением цилиндра является квадрат, диагональ которого равна 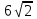 см. Найдите объем цилиндра. см. Найдите объем цилиндра.Контрольная работа «Объемы тел» Вариант 3 • 1. Прямоугольный параллелепипед имеет размеры 15 см, 50 см и 36 см. Найдите ребро равновеликого ему куба. • 2. Сторона основания правильной треугольной призмы равна 10 см, боковое ребро 12 см. Найдите объем призмы. 3. Прямоугольник с боковой стороной 40 и основанием 50 является осевым сечением цилиндра. Найдите объем цилиндра. Контрольная работа «Объемы тел» Вариант 4 • 1 . Прямоугольный параллелепипед имеет размеры 15 см, 50 см и 36 см. Найдите ребро равновеликого ему куба. • 2. Сторона основания правильной треугольной призмы равна 5 см, боковое ребро 6 см. Найдите объем призмы. 3. Прямоугольник с боковой стороной 20 и основанием 25 является осевым сечением цилиндра. Найдите объем цилиндра. Контрольная работа «Векторы. Метод координат в пространстве» Основная цель контрольной работы: выявить уровень усвоения и прочность знаний по теме «Векторы. Метод координат в пространстве» Вариант 1 Найдите координаты вектора 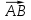 , если А(5; -1; 3), В(2; -2; 4). , если А(5; -1; 3), В(2; -2; 4).Даны векторы 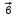 {3; 1; -2} и {3; 1; -2} и 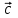 {1; 4; -3}. Найдите {1; 4; -3}. Найдите 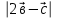 . .Найдите угол между прямыми АВ и СD, если А(3; -1; 3), В(3; -2; 2), С(2; 2; 3) и D(1; 2; 2). Вершины Δ АВС имеют координаты: А( -2; 0; 1 ), В( -1; 2; 3 ), С( 8; -4; 9 ). Найдите координаты вектора 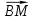 , если ВМ – медиана ∆АВС. , если ВМ – медиана ∆АВС.Даны векторы 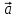 , , 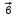 и и 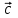 , причем: , причем: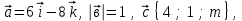 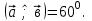 Найти: а) 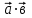 ; б) значение т, при котором ; б) значение т, при котором 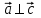 . .Контрольная работа «Векторы. Метод координат в пространстве» Вариант 2 Найдите координаты вектора 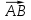 , если А(6; 3; -2), В(2; 4; -5). , если А(6; 3; -2), В(2; 4; -5).Даны векторы 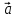 {5; -1; 2} и {5; -1; 2} и 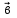 {3; 2; -4}. Найдите {3; 2; -4}. Найдите 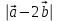 . .Найдите угол между прямыми АВ и СD, если А(1; 1; 2), В(0; 1; 1), С(2; -2; 2) и D(2; -3; 1). Даны векторы 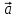 , , 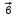 и и 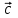 , причем: , причем: 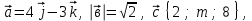 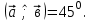 Найти: а) 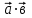 ; б) значение т, при котором ; б) значение т, при котором 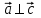 . .Вершины ∆АВС имеют координаты: А ( -1; 2; 3 ), В ( 1; 0; 4 ), С ( 3; -2; 1 ). Найдите координаты вектора 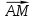 , если АМ – медиана ∆АВС. , если АМ – медиана ∆АВС. |
