Часть 2. Контрольная работа, выполненная не в соответствии с этими указаниями, не рассматривается и возвращается студенту

• Название: Контрольная работа, выполненная не в соответствии с этими указаниями, не рассматривается и возвращается студенту
• Дата: 21.11.2021
• Размер: 0.96 Mb.
• Имя файла: Часть 2.docx
• Тип: Контрольная работа; #277619
• страница: 6 из 6

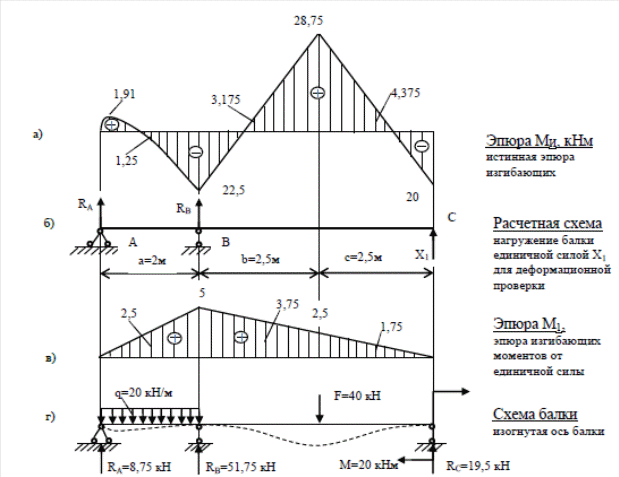Рис.109 – Деформационная проверка балки.
Из уравнений равновесия балки (Рис.109, б) определим реакции опор R_A и R_B.

Минус R_В показывает, что реакция опоры направлена вниз. Делаем проверку.

Реакции опор R_A и R_B определены верно.

Учитывая, что балкa имеет два участка, изгибающий момент на первом участке равен:
При ; ; При ; .

Изгибающий момент на втором участке равен:
При ; ; При ; .

По полученным значениям строим эпюру изгибающих моментов от единичной силы Х₁ (Рис.109, в).

Определяем прогиб на опоре С перемножая эпюру изгибающих моментов от заданной нагрузки (Рис.109, а) на эпюру изгибающих моментов от единичной силы (Рис.109, в).

=
Эпюра изгибающих моментов построена верно.

10. 
    По эпюре изгибающих моментов определяем опасное сечение. В нашем случае это сечение, где действует сила F. Здесь действует максимальный по абсолютной величине изгибающий момент М_max=28,75 кНм. Для этого сечения по условию прочности по нормальным напряжениям подбираем балку двутаврового сечения:
    

;

По сортаменту для двутавров стальных горячекатанных ГОСТ8239-89 выбираем двутавр

№20

11. 
    Схема упругой линии балки показана на рис.109, г. При ее изображении следует иметь в виду, что при положительном изгибающем моменте (эпюра М_И рис.109, а) упругая линия балки имеет выпуклость вниз, при отрицательном моменте – вверх. При изображении упругой линии балки следует учитывать расположение опор балки, на которых прогибы балки равны нулю, следовательно, упругая линия будут проходить по опорным точкам.
    

Расчетно-графическое задание №9
К решению задачи следует приступить после изучения темы «Косой изгиб». При косом изгибе плоскость действия изгибающего момента «силовая плоскость» не совпадает ни с одной из главных плоскостей балки. Косой изгиб делится на плоский косой изгиб, когда упругая линия балки – плоская кривая и пространственный косой изгиб, когда упругая линия балки – пространственная кривая. Внешнюю нагрузку при косом изгибе можно разложить на горизонтальную и вертикальную составляющие.

Используя метод сечений, строятся эпюры изгибающих моментов в горизонтальной и вертикальной плоскостях, по которым определяются опасные или предположительно опасные сечения. Из условия равенства нулю нормальных напряжений определяется положение нейтральной оси (нулевой линии), которая разделяет поперечное сечение на растянутые и сжатые части. Тангенс наклона нулевой линии с осью Ох определяется как
Нормальные напряжения при косом изгибе пропорциональны расстоянию точки, где определяются нормальные напряжения до нулевой линии. Поэтому максимальные нормальные напряжения будут действовать в наиболее удаленных от нулевой линии точках поперечного сечения и для косого пространственного изгиба они определятся
для плоского косого изгиба, для балок сечение которых имеет две оси симметрии, (прямоугольник, двутавр) величина напряжений определится
Для опасных точек поперечного сечения записывается условие прочности балки.

Линейные и угловые перемещения балки (прогиб и угол поворота поперечных сечений балки) определяются в горизонтальных и вертикальных плоскостях, а общие величины определяются геометрическим суммированием.
Задача 9. Сложное сопротивление

Для деревянной балки прямоугольного поперечного сечения (bxh), требуется:

1. 
   Найти размеры поперечного сечения балки из условия прочности при [σ] =12 МПа.
   
2. 
   Построить эпюру распределения нормальных напряжений в опасном сечении.
   
3. 
   Определить прогиб в середине длины балки.
   

Данные для расчета приведены в табл.8 и рис.87.

Решение:

1. 
   Выбираем по таблице 9 и рис.87 исходные данные согласно варианта:
   

№ схемы		Внешняя нагрузка		Длина участка балки, м		Отношение размеров поперечного сечения
		F, кН		q, кН/м		М, кНм		а	b	с	h/b
1	20		20		40		1,6	2	1,4	1,5

2. 
   На отдельной странице чертим расчетную схему с указанием исходных данных (Рис. 108, а).
   
3. 
   Строим эпюры изгибающих моментов в вертикальной плоскости. Для этого изображаем расчетную схему балки с внешней нагрузкой в вертикальной плоскости (Рис.110, б). Из уравнений равновесия определяем реакции опор и
   

Проверка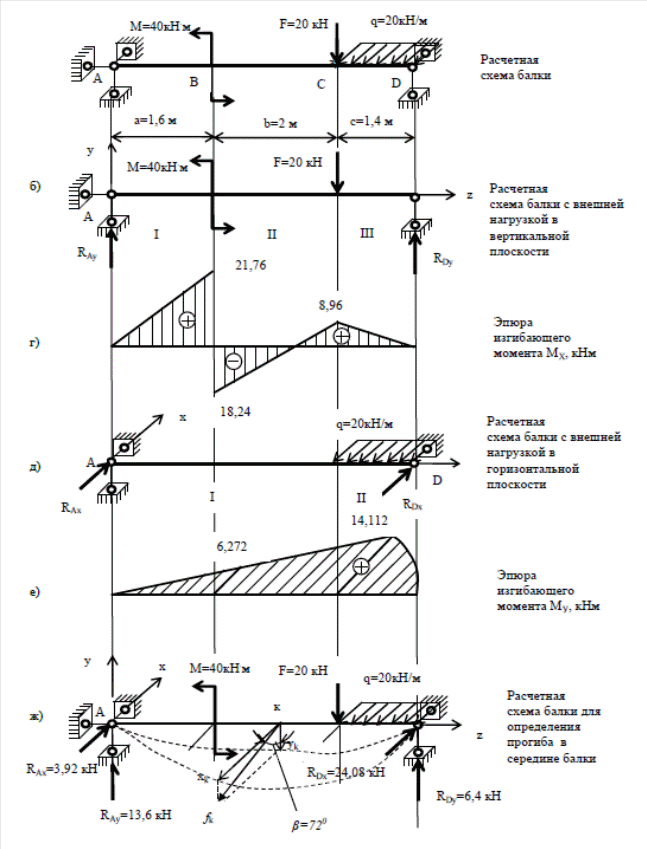


Рис.110 – Расчетные схемы и эпюры изгибающих моментов в горизонтальной и вертикальной плоскости
Делим балку на участки и определяем изгибающий момент на каждом участке. Результаты расчетов сводим в таблицу 23.

Таблица 23 - Расчет изгибающих моментов в вертикальной плоскости.

№ участка	≤ z ≤	Уравнение изгибающих моментов в вертикальной плоскости
I	RAy z1 0 ≤ z1 ≤ 1,6 м
II	1,6 ≤ z2 ≤ 3,6 м RAy z2 а	; ; =
III	RDy z3 0 ≤ z3 ≤ 1,4 м

По результатам расчетов строим эпюру изгибающих моментов М_X (Рис.110, в).

Строим эпюры изгибающих моментов в горизонтальной плоскости. Для этого изображаем расчетную схему балки с внешней нагрузкой в горизонтальной плоскости (Рис.110, г). Из уравнений равновесия определяем реакции опор и

Проверка

Делим балку на участки и определяем изгибающий момент на каждом участке. Результаты расчетов сводим в таблицу 24.

Таблица 24 - Расчет изгибающих моментов в горизонтальной плоскости.

№ участка	≤ z ≤	Уравнение изгибающих моментов в горизонтальной плоскости
I	RAх z1 0 ≤ z1 ≤ 3,6 м
II	q RDх z3 0 ≤ z3 ≤ 1,4 м

По результатам расчетов строим эпюру изгибающих моментов М_У (Рис.110, е).

4. 
   Находим размеры поперечного сечения балки из условия прочности при [σ] =12 МПа. Для этого по эпюрам изгибающих моментов определяем предположительно опасные сечения. Ими являются сечения В и С.
   

Изгибающие моменты в сечении В:

Изгибающие моменты в сечении С:

Условие прочности для предположительно опасных сечений запишется в виде:
Учитывая, что а и отношение , получим:
откуда .
Определяем размеры поперечного сечения балки в сечении В:

Определяем размеры поперечного сечения балки в сечении С:


Принимаем больший из размеров и по технологическим соображениям округляем до целых сантиметров в большую сторону. Окончательно имеем:

5. Строим эпюру распределения нормальных напряжений в опасном сечении В.

Предварительно определяем отношение осевых моментов инерции сечения:
Положение нулевой линии в сечении определится как:

Угол наклона нулевой линии к оси Х составляет Напряжения в опасных точках А и В поперечного сечения (Рис.111) равны: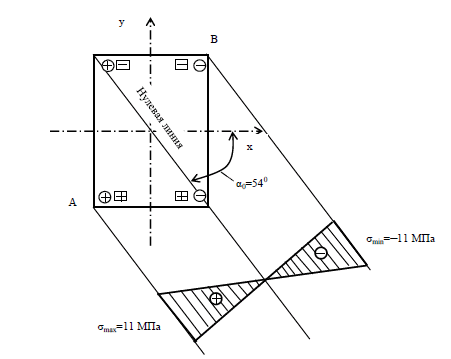




Рис.111 – Положение нулевой линии и распределение нормальных напряжений в поперечном сечении балки при косом изгибе

5. 
   Определение полного прогиба балки в середине балки (рис.110, ж; точка к) может быть выполнена по методу начальных параметров (или иным способом).
   

Определим прогиб в плоскости yoz методом начальных параметров. Уравнение прогибов запишется в виде:;

где , а определится из условия: при ;

Тогда прогиб в точки к (у_к) определится при z=2,5 м:

.

Откуда .

Определим прогиб в плоскости xoz методом начальных параметров. Уравнение прогибов запишется:;

где , а определится из условия: при ;

Откуда:
Тогда при z=2,5 м величина прогиба точки к (х_К) балки в горизонтальной плоскости;


Полный прогиб в точки к (f_K) будет равен:
Направление прогиба определится углом : 3,045; (Рис.110, ж).

Расчетно-графическое задание №10
К решению задачи следует приступить после изучения темы «Изгиб с кручением». Одновременное действие в поперечном сечении бруса изгибающего и крутящего момента приводит к возникновению в опасной точке нормальных и касательных напряжений, что характеризует плоского напряженного состояния. В этом случае оценку прочности бруса ведут по эквивалентным напряжениям с использованием теорий прочности. Наиболее часто используются следующие теории прочности:

1. 
   Теория наибольших касательных напряжений (третья теория прочности). Применяется для материалов одинаково работающих на растяжение и сжатие:
   

2. 
   Энергетическая теория прочности (четвертая теория прочности). Применяется для пластичных материалов одинаково работающих на растяжение и сжатие:
   

3. 
   Теория прочности Мора. Применяется для материалов, неодинаково работающих на растяжение и сжатие – легированная сталь, чугун и др. материалы.
   

где k – отношение предела прочности на на растяжение к пределу прочности на сжатие.