Часть 2. Контрольная работа, выполненная не в соответствии с этими указаниями, не рассматривается и возвращается студенту
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
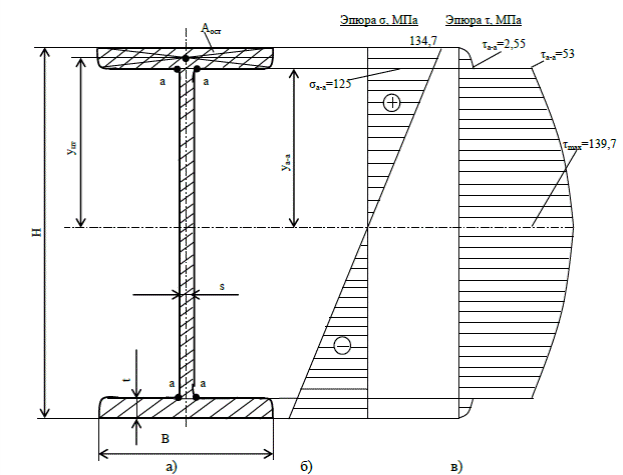 Рис.102 – Поперечное сечение двутавра и эпюры нормальных и касательных напряжений В сечении а-а там, где стойка переходит в полку, действуют значительные значения нормальных σа-а=125 МПа и касательных τа-а=53 МПа напряжений. Для двутаврового сечения это наиболее слабое место, поэтому его следует проверить на прочность с использованием теории наибольших касательных напряжений: Условие прочности по эквивалентным напряжениям выполняется. Задача 6 (б). Расчет балки на изгиб. Для заданной балки требуется: 1. Из условий равновесия балки определить реакции опор. 2. Построить эпюры поперечных сил и изгибающих моментов. 3. Из расчета на прочность по нормальным напряжениям подобрать двутавровое, круглое и прямоугольное сечения и сравнить массу балки каждого профиля, если материал балки - сталь 3, [σ] =160 МПа, Е = 2·105 МПа. 4. Для опасного сечения балки двутаврового сечения проверить прочность по эквивалентным напряжениям с использованием теории наибольших касательных напряжений. 5. Для консольно закрепленной балки двутаврового сечения (рис.7) определить прогиб и угол поворота свободного конца балки. Данные для расчета приведены в табл.6 и рис.85. Решение: Выбираем по таблице 6 исходные данные согласно варианта:
На отдельной странице чертим расчетную схему с указанием исходных данных (Рис. 101, а). На опорах балки будут возникать реакции опор RA и RВ. Из уравнения равновесия балки определяем реакции опор балки RA и RВ. Для этого для плоской системы составляем три уравнения равновесия: Указываем числовое значение реакций опор на расчетной схеме и делаем проверку. Реакции опор МВ и RВ определены верно. 4. Делим балку на участки на участки. Границами участков являются точки приложения внешних сил, начало и конец приложения распределенных усилий, плоскости приложения внешних моментов и сечения, где изменяется площадь поперечного сечения балки. Проводим через границы участков линии, перпендикулярные оси балки. 5. Присваиваем номер каждому участку. Нумерацию участков начнем с левого конца балки. 6. Методом сечений (правило РОЗУ) определяем поперечную силу Q и изгибающий момент МИ на каждом участке. Расчет поперечных сил Q и изгибающих моментов МИ сводим в таблицу 22.  Рис.103 – Расчетные схемы и эпюры поперечных сил и изгибающих моментов Таблица 22- Расчет поперечных сил и изгибающих моментов
По полученным значениям строим эпюру поперечных сил Q (Рис.103, б) и изгибающих моментов МИ (Рис.103, в). Пользуясь эпюрой изгибающих моментов, изображаем возможную изогнутую ось балки, учитывая, что при положительном изгибающем моменте ось балки имеет выпуклость вниз, а при отрицательном моменте – вверх (Рис.103, г). 7. По эпюре изгибающих моментов определяем опасное сечение. В нашем случае это сечение заделки, где изгибающий момент достигает максимального значения: МИmax= 23,45 кН.м. Из расчета на прочность по нормальным напряжениям подбираем двутавровое поперечное сечение: откуда . По ПРИЛОЖЕНИЮ для сортамента «Двутавры стальные горячекатанные (ГОСТ 8239-89)» выбираем двутавр №18а у которого , это ближайшее большее значение к расчетному моменту сопротивления сечения. Выписываем геометрические характеристики двутавра №18а (Таблица 23). Таблица 23 – Геометрические характеристики двутавров №№18а, 20.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||







