Часть 2. Контрольная работа, выполненная не в соответствии с этими указаниями, не рассматривается и возвращается студенту
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
Подбираем диаметр круглого поперечного сечения балки с учетом, что осевой момент сопротивления балки круглого поперечного сечения равен: ; Подбираем размеры прямоугольного поперечного сечения балки с учетом, что h/b=2, а Из условия равнопрочности сравним вес балок с различным поперечным сечением. Вес балки можно определить как произведение объема балки на величину плотности материала. Учитывая, что длина и плотность материала балки одинакова, получим, что для сравнения веса балки достаточно сравнить их площади поперечных сечений. см2 - для двутаврого сечения; АО = – для круглого поперечного сечения; А□ = b.h =6,04.12,08 = 72,96 см2 – для прямоугольного поперечного сечения. Получили, что самым выгодным поперечным сечением при изгибе является двутавр, за ним следует прямоугольное поперечное сечение и затем круглое поперечное сечение. Экономия материала при использовании двутаврового сечения по сравнению с круглым поперечным сечением балки составит раза, а прямоугольного - раза. 8. Для опасного сечения балки двутаврового сечения проверим прочность по эквивалентным напряжениям с использованием теории наибольших касательных напряжений. Для этого вычертим в масштабе 2:1 поперечное сечение двутавровой балки (Рис.103, а). Распределение нормальных напряжений по поперечному сечению подчиняются закону . При у=0; При ; МПа. . При МПа Строим эпюру распределения нормальных напряжений по поперечному сечению (Рис.104, б). Распределение касательных напряжений по поперечному сечению подчиняются закону. При ; При МПа При МПа По полученным значениям строим эпюру распределения касательных напряжений по поперечному сечению (Рис.104,в). 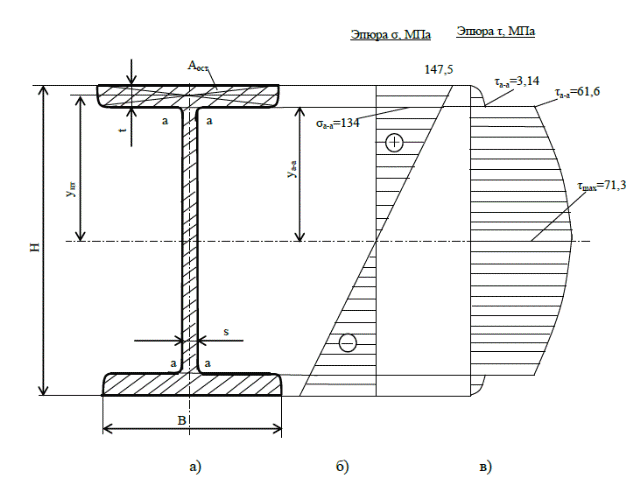 Рис.104 – Поперечное сечение двутавра и эпюры нормальных и касательных напряжений Рис.104 – Поперечное сечение двутавра и эпюры нормальных и касательных напряженийПроводим проверку прочности двутавра по сечению а-а там, где стойка переходит в полку, по теории наибольших касательных напряжений: Условие прочности по эквивалентным напряжениям не выполняется, поэтому выбираем двутавр №20, геометрические характеристики которого приведены в таблице 23. Проводим повторный расчет эквивалентных напряжений для двутавра №20. Распределение нормальных напряжений: . При у=0; При ; МПа. . При МПа Распределение касательных напряжений по поперечному сечению. При ; При МПа При МПа Эквивалентные напряжения в сечении а-а по теории наибольших касательных напряжений: . Окончательно принимаем двутавр №20 ГОСТ 8239-89. 9.Для консольно закрепленной балки двутаврового сечения определяем прогиб и угол поворота свободного конца балки. Прогиб и угол поворота поперечных сечений можно определить различными способами. Здесь рассмотрим метод начальных параметров и способ перемножения эпюр (способ Верещагина). 9.1. Метод начальных параметров. Поместим начало координат в левый конец балки (Рис.105). 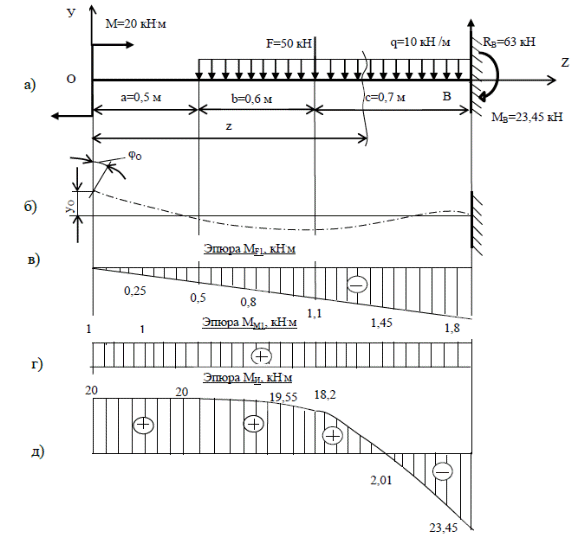 Рис.105 – Расчетные схемы и эпюры изгибающих моментов Запишем универсальные уравнения метода начальных параметров: ; . Применительно для нашей балки они будут иметь вид: ; + ; + Определим величину и из условия, что при z=1,8 м прогиб и угол поворота в сечении заделки будут равны нулю: ; 0 кН.м2; 7,81 кН.м3. С учетом начальных параметров универсальные уравнения для балки запишутся в виде: ; Тогда угол поворота свободного конца балки и прогиб уО будут равны: При z=0; м «Минус» показывает, что поперечное сечение поворачивается относительно своего первоначального положения по часовой стрелке. «Плюс» показывает, что прогиб направлен в противоположную сторону оси У. 9.2. Способ перемножения эпюр (способ Верещагина). Для определения угла поворота свободного конца балки необходимо перемножить эпюры изгибающих моментов от заданной нагрузки с эпюрами изгибающих моментов от единичного момента, приложенного на свободном конце балки. Для этого приложим к балке единичный момент (Рис.103, е). Методом сечений определяем изгибающие моменты: Стоим эпюру изгибающих моментов (Рис.105, г). Величина угла поворота свободного конца балки определится по формуле: Для упрощения расчетов при перемножении эпюр воспользуемся формулой Симпсона. Тогда: рад. «Плюс» показывает, что угол поворота совпадает с направлением единичного момента. Для определения прогиба свободного конца балки необходимо перемножить эпюры изгибающих моментов от заданной нагрузки с эпюрами изгибающих моментов от единичной силы, приложенной на свободном конце балки. Для этого приложим к балке единичную силу (Рис.103, д). Методом сечений определяем изгибающие моменты: Определяем изгибающие моменты в начале, середине и конце каждого участка. По полученным значениям строим эпюру изгибающих моментов (Рис.105, в). Величина прогиба свободного конца балки определится по формуле: Cогласно формуле Симпсона прогиб равен: «Минус» показывает, что прогиб направлен в противоположную сторону единичной силы. Результаты вычислений угла поворота и прогиба балки, выполненные разными способами дают одинаковые результаты. Расчетно-графическое задание №7 К решению задачи следует приступить после изучения темы «Статически неопределимые системы». Для решения статически неопределимых систем, кроме уравнений равновесия необходимо составить дополнительные уравнения совместности деформаций и решить статическую, геометрическую и физическую сторону задачи. Задача 7. Расчет статически неопределимых систем Для заданного абсолютно жесткого бруса, имеющего шарнирно-неподвижную опору и две тяги из упругопластического материала, нагруженного переменной по значению силой F (рис.86, табл.7) требуется: 1. Вычертить расчетную схему в определенном масштабе. 2. Найти зависимости от силы F значения усилий в тягах. 3. Определить в процессе увеличения силы F ее значение, при котором напряжение в одной из тяг достигнет предела текучести. 4. Определить в процессе увеличения силы F ее значение, при котором несущая способность обеих тяг будет исчерпана. 5. Найти значение грузоподъемности из расчета по методу допускаемых напряжений и методу разрушающих нагрузок если коэффициент запаса прочности k = 1,5, допускаемые напряжения [σ]=σт/k, модуль упругости Е = 2.105 МПа и предел текучести материала тяг σт=240 МПа. Сопоставить результаты и сделать выводы. Решение: Выбираем по таблице 7 исходные данные согласно варианта:
На отдельной странице чертим расчетную схему с указанием исходных данных (Рис. 101, а). На опорах балки будут возникать реакции опор RA и RВ. 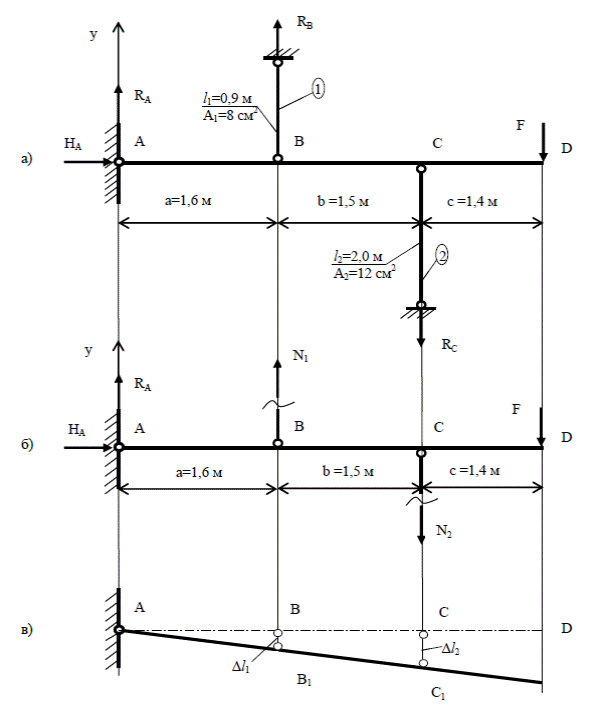 Рис.106 – Расчетные схемы статически неопределимой системы Решаем статическую сторону задачи. Определяем степень статической неопределимости системы: ; где количество неизвестных реакций связи (НА, ); у количество независимых уравнений равновесия для плоской системы. Система один раз статически неопределима. Решаем геометрическую сторону задачи. Для этого выбираем основную систему. Так как расчет реакций опоры А здесь не предполагается, то реакции НА, не вычисляем. Отбрасываем опоры В и С и заменяем из реакциями стержней N1 и N2 (Рис.106, б). Направление реакций стержней делаем положительным, то есть предполагаем, что стержни испытывают деформацию растяжения (Если в результате решения уравнений получим знак минус, значит стержень испытывает деформацию сжатия). Записываем для основной системы уравнение равновесия: Физическая сторона задачи. Составляем уравнение совместности деформации системы. Для этого системе придаем возможное перемещение (Рис.106, в). Используя подобие треугольников АВВ1 и АСС1 получим уравнение совместности деформации: , где абсолютные удлинения стержней 1 и 2, которые согласно закону Гука будут равны: Подставляя полученные выражения в уравнение совместности деформации получим: Откуда . Подставим полученное выражение в уравнение равновесия системы: Получили значения усилий и в виде функции от . Стержень 1 испытывает деформацию растяжения, а стержень 2 деформацию сжатия. Установим опасное состояние системы. Для этого определим нормальные напряжения в каждом стержне: Учитывая, что пластичные материалы одинаково работают на растяжение и сжатие сравнение напряжений производим по модулю. Получим а значит, в стержне 2 при возрастании силы F стержень 2 первым достигнет стадии текучести материала и с точки зрения метода допускаемых напряжений это состояние конструкции будет опасным и для него должно выполняться условие прочности: Тогда , = При этой нагрузке в стержне 1 рабочие напряжения составят величину = что меньше допускаемых напряжений на . Как видно, стержень 1 существенно недогружен и вся конструкция далека от разрушения, система не потеряла своей несущей способности. 5.Определим допускаемую нагрузку по методу разрушающих (предельных) нагрузок. Увеличивая внешнюю силу F и полагая, что стержень 2 постиг предела текучести и в дальнейшем, при повышении силы F усилие в стержне 2, равное будет неизменным (согласно диаграммы Прандтля рис.108), а усилие в стержне 1 будет возрастать до значения и стержень 1 вынужденно будет воспринимать увеличивающую нагрузку. В момент достижения материалом стержня 1 нормальных напряжений равных пределу текучести вся конструкция постигнет предельного состояния.  Рис.107 – Диаграмма Прандтля Условие предельного состояния системы запишем исходя из уравнения равновесия: Откуда Допустимое значение силы по методу разрушающих нагрузок определится Сравним результаты расчетов метода допускаемых напряжений и метода разрушающих нагрузок. Получим, что по методу разрушающих нагрузок мы используем дополнительные прочностные резервы конструкции, что позволило увеличить допускаемую силу по сравнению с методом допускаемых напряжений на . Расчетно-графическое задание №8 К решению задачи следует приступить после изучения темы «Расчет статически неопределимых балок». Для решения статически неопределимых балок, кроме уравнений равновесия необходимо составить дополнительные уравнения совместности деформаций и решить статическую, геометрическую и физическую сторону задачи. Дополнительные уравнения совместности деформаций для статически неопределимых балок выполняются по методу сил, где в качестве неизвестных принимаются усилия, заменяющие действие отброшенных (лишних) связей. Задача 8. Расчет статически неопределимых балок Для статически неопределимой балки постоянного поперечного сечения требуется: Построить эпюры изгибающих моментов Ми, и поперечных сил Q. Подобрать номер прокатного двутавра из условия прочности по нормальным напряжениям при [σ] =160 МПа. Изобразить вид упругой оси балки исходя из эпюры изгибающих моментов и условий закрепления балки. Данные для расчета приведены в табл.8 и рис.87. Решение: Выбираем по таблице 8 исходные данные согласно варианта:
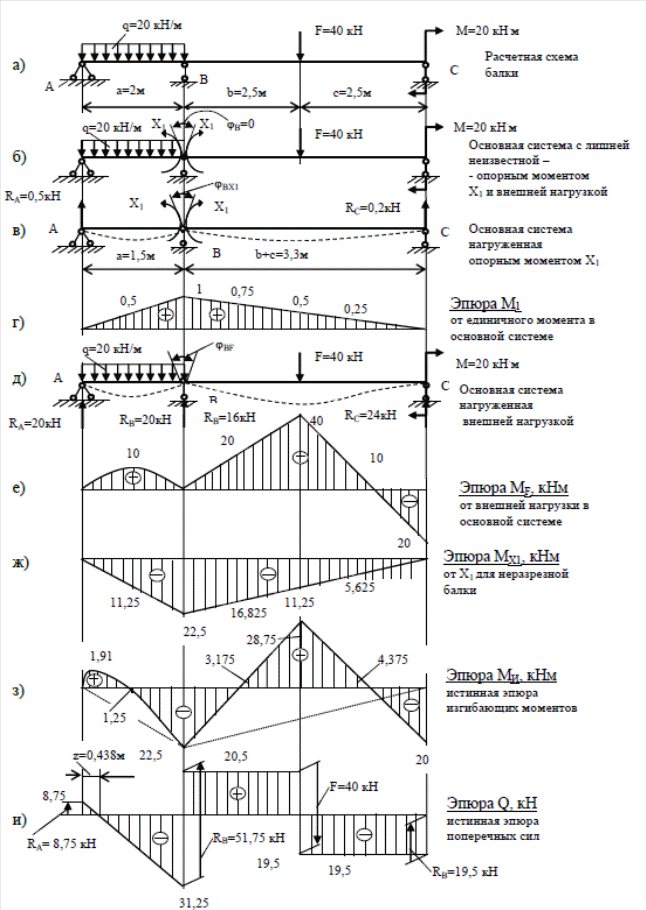 Рис.108 – Расчетные схемы и эпюры изгибающих моментов и поперечных сил для статически неопределимой балки. На отдельной странице чертим расчетную схему с указанием исходных данных (Рис. 108, а). Решаем статическую сторону задачи. Определяем степень статической неопределимости системы: ; где количество неизвестных реакций связи (НА, ); у количество независимых уравнений равновесия для плоской системы. Система один раз статически неопределима. Решаем геометрическую сторону задачи. Для этого выбираем основную систему. Основную систему выбираем в виде двух шарнирно опертых балок (Рис.108, б) путем разреза балки шарниров под опорой В. Такая основная система для многопролетной балки называется рациональной. Физическая сторона задачи. Составляем уравнение совместности деформации балки исходя из того, что за лишнее неизвестное принимаем изгибающий момент во введенном шарнире. Тогда исходя из непрерывности упругой линии балки уравнение совместности деформации в форме канонического уравнения метода сил будет иметь вид где - искомый изгибающий момент в опорном сечении Б; - угловое перемещение (угол поворота поперечного сечения) в опорном сечении Б от ; – угловое перемещение (угол поворота поперечного сечения) в опорном сечении Б от внешней нагрузки. Для определения коэффициентов необходимо построить эпюры изгибающих моментов от единичного момента и от внешней нагрузки в основной системе. Прикладываем к основной системе единичный момент (Рис.108, в). Балку представляем состоящей из двух балок. Рассмотрим левую часть балки основной системы. Определяем из уравнений равновесия реакции опор для левой части балки. Минус RВ показывает, что реакция опоры направлена вниз. Делаем проверку. Реакции опор RA и RВ определены верно. Учитывая, что левая часть балки имеет только один участок, изгибающий момент на нем будет равен: При ; ; При ; . Рассмотрим правую часть балки основной системы. Определяем из уравнений равновесия реакции опор для левой части балки. Минус RВ показывает, что реакция опоры направлена вниз. Делаем проверку. Реакции опор RB и RC определены верно. Учитывая, что правая часть балки имеет только один участок, изгибающий момент на нем будет равен: При ; ; При ; . По полученным значениям строим эпюру изгибающих моментов от единичного момента (Рис.108, г). Прикладываем к основной системе внешнюю нагрузку (Рис.108, д). Балку представляем состоящей из двух балок. Рассмотрим левую часть балки основной системы на которую действует только распределенная нагрузка. Определяем из уравнений равновесия реакции опор для левой части балки. Учитывая симметричность действия распределенной нагрузки имеем Делаем проверку. Реакции опор RA и RВ определены верно. Методом сечений определяем изгибающий момент для левой части балки который будет равен: При ; ; При ; При ; . Рассмотрим правую часть балки основной системы. Определяем из уравнений равновесия реакции опор для левой части. Проверка Реакции опор RB и RC определены верно. Учитывая, что правая часть балки имеет два участка, изгибающий момент на первом участке равен: При ; ; При ; . Изгибающий момент на втором участке равен: При ; ; При ; . По полученным значениям строим эпюру изгибающих моментов от внешней нагрузки (Рис.108, е). Определение коэффициентов и выполняем по формуле Мора. Для упрощения расчетов при перемножении эпюр можно использовать формулу Симпсона. Определяем коэффициент = Определяем коэффициент = Значение определяем из канонического уравнения метода сил: Строим истинную эпюру изгибающих моментов от умножая значение ординаты единичной эпюры М1 на значение Х1= (Рис.108, ж) и складывая ее алгебраически с эпюрой изгибающих моментов от действующей нагрузки в основной системе получим окончательную (расчетную эпюру изгибающих моментов (Рис.108, з). Ординаты истинной эпюры поперечных сил Q могут быть определены для каждого участка по формуле: где интенсивность распределенной нагрузки на рассматриваемом участке (если нагрузка отсутствует, то q=0); длина рассматриваемого участка; , ординаты моментов на правом и левом конце участка, которые берутся со своими знаками. Для нашей балки имеем: Участок I Участок II: Участок III: По полученным значениям строим эпюру поперечных сил (Рис.108, и). Проводим проверку правильности построения эпюры поперечных сил и изгибающих моментов. По эпюре Q определяем опорные реакции балки. Так как эпюра Q представляет собой силовой многоугольник, то начиная построение эпюры поперечных сил с левого конца балки, скачки на эпюре поперечных сил и направление этих скачков будет соответствовать направлению и величине внешних сил и реакций опор на расчетной схеме балки. На (Рис.108, и) показано направление и величина реакций опор балки. Выполняем статическую проверку балки: Уравнение равновесия балки выполняется, значит расчет верен. На первом участке балки эпюра поперечных сил равна нулю, а значит эпюра изгибающих моментов в этом сечении имеет экстремум. Определим абсциссу сечения из условия Величина изгибающего момента в этом сечении будет равна: При Проводим деформационную проверку балки. Для этого отбрасываем одну из опор, например, опору С (Рис.109, б) и зная, что на опоре С прогиб равен нулю, вычислим его по методу Мора. Если прогиб на опоре ( равен нулю, то эпюра изгибающих моментов построена верно, если 0, расчет балки содержит ошибки и должен быть переработан. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
