Часть 2. Контрольная работа, выполненная не в соответствии с этими указаниями, не рассматривается и возвращается студенту
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
Выписываем из сортамента размеры и геометрические характеристикистального горячекатанного швеллера с прямыми полками №10 ГОСТ 8240-89 и сводим в табл. 19. Таблица 19- Геометрические характеристики стального горячекатанного швеллера
Выписываем из сортамента размеры и геометрические характеристики горячекатанного стального равнополочного уголка №7 ГОСТ 8509-93 и сводим в табл.20. 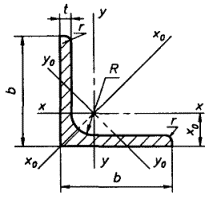 Таблица20 – Геометрические характеристики горячекатанного стального равнополочного уголка
На отдельной странице чертим составное сечение в масштабе 1:1 (Рис. 99) с указанием исходных данных. Учитывая, что швеллер занимает горизонтальное положение в составном сечении справочные значения для осей х-х и у-у меняем местами. Отмечаем центры тяжести швеллера через С1 и равнополочного уголка через С2 и проводим через них центральные оси ХС1, УС1 и ХС2, УС2. Определяем положение центра тяжести главных осей составного сечения. Для этого выбираем вспомогательные оси Х и У, проведенные через крайнюю левую точку составного сечения (в качестве вспомогательных осей можно выбрать любые оси параллельные или совпадающие с осями ХСi, УСi) и определяем расстояния от вспомогательных осей до центра тяжести каждого из сечений. = ; = см Координаты центра тяжести составного сечения определим по формулам:  Рис.99 – Cхема составного сечения Для проверки правильности определения положения центра тяжести составного сечения, нужно соединить центры тяжести О1 и О2 составляющих сечений. Центр тяжести составного сечения должен лежать на этой линии. Через полученные координаты проводим через центр тяжести центральные оси ХС и УС. Находим расстояния между центральными осями составного сечения ХС и УС и центральными осями швеллера ХС1, УС1 и уголка ХС2, УС2. Определяем значение осевых моментов инерции относительно центральных осей ХС и УС. Величина осевых моментов инерции сечения определится по формулам: Величина центробежного момента инерции сечения определится по формуле: Центробежный момент швеллера равен нулю, так как ось УС1 является осью симметрии сечения. Центробежный момент инерции уголка определится из формулы: . Знак центробежного момента инерции уголка определяется по расположению уголка в составном сечении в пространстве и берется согласно рис.100. 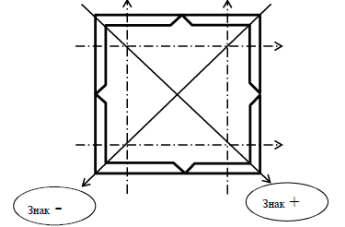 Рис.100 – Выбор знака центробежного момента инерции уголка Определяем положение главных центральных осей инерции сечения: . ; . Проводим главные центральные оси инерции. Для этого оси ХС и УС поворачивает по часовой стрелке на угол . Это оси V и Н. Определяем главные центральные моменты инерции относительно осей V и Н. Проверка Вычисления главных центральных моментов инерции выполнены верно. Определяем главные радиусы инерции: Откладывая по оси V значение радиуса инерции а по оси Н рисуем эллипс инерции на составном сечении. Расчетно-графическое задание №6 К решению задачи следует приступить после изучения темы «Чистый и поперечный прямой изгиб». При чистом изгибе в поперечных сечениях возникает только изгибающий момент, а при поперечном – изгибающий момент и поперечная сила. Особое внимание необходимо обратить на правило знаков для поперечной силы и изгибающего момента при составлении уравнений равновесия и построении эпюр поперечных сил и изгибающих моментов. Необходимо изучить вопрос о напряжениях, возникающих при изгибе в поперечных сечениях балки и распределении напряжений по поперечному сечению. Понять, как определяется опасное сечение балки и опасные точки поперечного сечения, которые лимитируют прочность балки. В зависимости от вида изгиба, поперечного сечения, распределения нормальных и касательных напряжений производится оценка прочности балки по нормальным, касательным или эквивалентным напряжениям. Следует изучить вопросы, связанные с определением линейных и угловых перемещений балки (прогиб, и угол поворота поперечных сечений балки). Освоить методы определения перемещений балки при помощи универсальных уравнений метода начальных параметров, формулы Мора и способом Верещагина (способ перемножения эпюр). Задача 6 (а). Расчет балки на изгиб. Для заданной балки требуется: 1. Из условий равновесия балки определить реакции опор. 2. Построить эпюры поперечных сил и изгибающих моментов. Используя эпюру изгибающих моментов построить изогнутую ось балки. 3. Из расчета на прочность по нормальным напряжениям подобрать двутавровое, круглое и прямоугольное сечения и сравнить массу балки каждого профиля, если материал балки - сталь 3, [σ] =160 МПа, Е = 2·105 МПа. 4. Для опасного сечения балки двутаврового сечения проверить прочность по эквивалентным напряжениям с использованием теории наибольших касательных напряжений. Данные для расчета приведены в табл.6 и рис.85. Решение: Выбираем по таблице 6 исходные данные согласно варианта:
На отдельной странице чертим расчетную схему с указанием исходных данных (Рис. 101, а). На опорах балки будут возникать реакции опор RA и RВ. Из уравнения равновесия балки определяем реакции опор балки RA и RВ. Для этого для плоской системы составляем три уравнения равновесия: Минус RВ показывает, что реакция опоры направлена в противоположную сторону. Зачеркиваем первоначальное направление реакции опоры и направляем ее в противоположную сторону. Указываем числовое значение реакций опор и делаем проверку. Реакции опор RA и RВ определены верно. 4. Делим балку на участки на участки. Границами участков являются точки приложения внешних сил, начало и конец приложения распределенных усилий, плоскости приложения внешних моментов и сечения, где изменяется площадь поперечного сечения балки. Проводим через границы участков линии, перпендикулярные оси балки. 5. Присваиваем номер каждому участку. Нумерацию участков можно вести с любого конца балки, если определены реакции опор. Для нашей задачи нумерацию участков начнем с левого конца балки. 6. Методом сечений (правило РОЗУ) определяем поперечную силу Q и изгибающий момент МИ на каждом участке. Расчет поперечных сил Q и изгибающих моментов МИ сводим в таблицу 21. 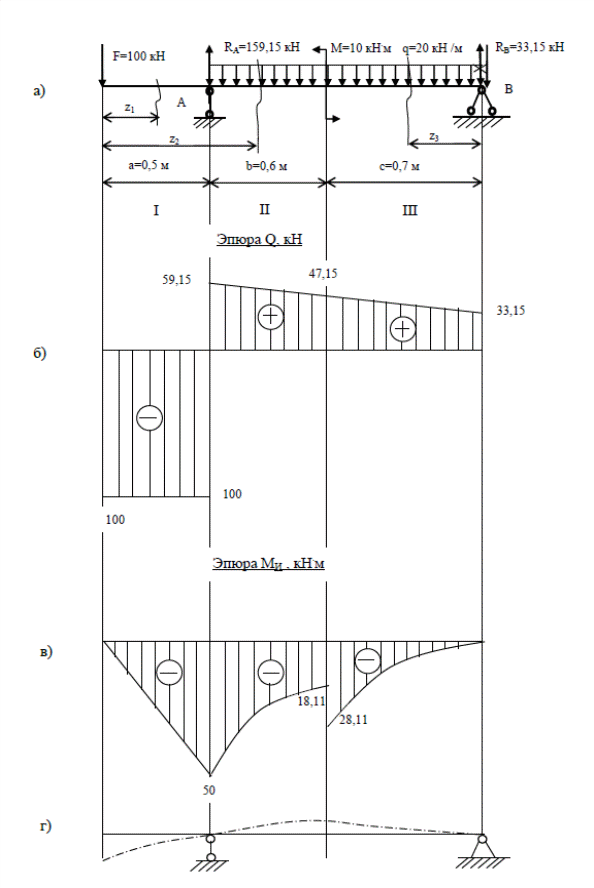 Рис.101 – Расчетная схема и эпюры поперечных сил и изгибающих моментов Таблица 20 - Расчет поперечных сил и изгибающих моментов.
По полученным значениям строим эпюру поперечных сил Q (Рис.101, б) и изгибающих моментов МИ (Рис.101, в). Пользуясь эпюрой изгибающих моментов, изображаем возможную изогнутую ось балки, учитывая, что при положительном изгибающем моменте ось балки имеет выпуклость вниз, а при отрицательном моменте – вверх (Рис.101, г). 7.По эпюре изгибающих моментов определяем опасное сечение. В нашем случае это сечение под опорой А, где изгибающий момент достигает максимального значения: МИmax=50 кН.м. Из расчета на прочность по нормальным напряжениям подбираем двутавровое поперечное сечение: откуда . Согласно ПРИЛОЖЕНИЯ по сортаменту «Двутавры стальные горячекатанные (ГОСТ 8239-89)» выбираем двутавр №27 у которого , это ближайшее большее значение к расчетному моменту сопротивления сечения. Выписываем геометрические характеристики двутавра №27 (Таблица 21). Таблица 21 – Геометрические характеристики двутавра №27
Подбираем диаметр круглого поперечного сечения балки с учетом, что осевой момент сопротивления балки круглого поперечного сечения равен: ; Подбираем размеры прямоугольного поперечного сечения балки с учетом, что h/b=2, а Из условия равнопрочности сравним вес балок с различным поперечным сечением. Вес балки можно определить как произведение объема балки на величину плотности материала. Учитывая, что длина и плотность материала балки одинакова, получим, что для сравнения веса балки достаточно сравнить их площади поперечных сечений. см2 - для двутаврого сечения; АО = – для круглого поперечного сечения; А□ = b.h =7,84.15,68 = 122,93 см2 – для прямоугольного поперечного сечения. Получили, что самым выгодным поперечным сечением при изгибе является двутавр, за ним следует прямоугольное поперечное сечение и затем круглое поперечное сечение. Экономия материала при использовании двутаврового сечения по сравнению с круглым поперечным сечением балки составит раза, а прямоугольного - раза. 8.Для опасного сечения балки двутаврового сечения проверим прочность по эквивалентным напряжениям с использованием теории наибольших касательных напряжений. Для этого вычертим в масштабе 2:1 поперечное сечение двутавровой балки (Рис.102, а). Распределение нормальных напряжений по поперечному сечению подчиняются закону . При у=0; При ; МПа. . При МПа Строим эпюру распределения нормальных напряжений по поперечному сечению (Рис.102, б). Распределение касательных напряжений по поперечному сечению подчиняются закону. При ; При МПа При МПа По полученным значениям строим эпюру распределения касательных напряжений по поперечному сечению (Рис.102,в). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






