Часть 2. Контрольная работа, выполненная не в соответствии с этими указаниями, не рассматривается и возвращается студенту
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
VII. ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ Студенты направления подготовки 20.03.01 «Техносферная безопасность» и 44.03.01 «Педагогическое образование», профиль: «Технология» выполняют задачи №1,2,3,4,5,6,11 контрольной работы. Студенты направления подготовки 13.03.02 «Электроэнергетика и электротехника» выполняют задачи №1,3,4,5,6,7 контрольной работы. Студенты направления подготовки - 13.03.02 «Нефтегазовое дело» и «Строительство» выполняют задачи №1,3,4,5,6,7 ,8,9,10,11,12,13 контрольной работы. Студенты направления подготовки - 13.03.02«Автомобили и автомобильное хозяйство» выполняют задачи №1,3,4,5,6,7,8, 10,11, 13 Расчетно-графическое задание №1 К решению задачи можно приступить после изучения темы: «Основные понятия и определения, растяжение и сжатие». Первая задача требует умения строить эпюры продольных сил, нормальных напряжений, перемещений стержня и проводить расчеты на прочность и жесткость стержня при деформации растяжение (сжатие). При работе бруса на растяжение (сжатие) в его поперечных сечениях возникает только продольная сила N, остальные внутренние силовые факторы равны нулю. Она определяется с помощью метода сечений (правило РОЗУ). Продольная сила N в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций внешних сил на его продольную ось, действующих на оставшуюся часть стержня. Правило знаков для продольной силы: Продольная сила N положительна, если относительно рассматриваемого сечения внешняя сила растягивает стержень и продольная сила отрицательна, если внешняя сила сжимает стержень. При растяжении (сжатии) стержня в его поперечных сечениях возникают нормальные напряжения (А - площадь поперечного сечения стержня). Изменение длины стержня (удлинение или укорочение) равно алгебраической сумме удлинений (укорочений) его отдельных участков и вычисляется по формуле: , где Ni, li, Аi - соответственно продольная сила, длина и площадь поперечного сечения i участка стержня; Е - модуль продольной упругости. Напряжения в наклонных сечениях стержня определяются по формулам: где угол между поперечным и наклонным сечениями. Условие прочности при растяжении (сжатии) Задача № 1. Расчет ступенчатого стержня. Для ступенчатого стержня (E = 2·105 MПa, σт = 240 МПа) необходимо определить: 1. Продольные силы по его длине и построить эпюру продольных сил. 2. Определить нормальные напряжения в поперечных сечениях и построить эпюру нормальных напряжений. 3. Определить коэффициент запаса прочности для опасного сечения. 4. Определить аналитически нормальное и касательное напряжения в опасном сечении на площадке, расположенной под углом 5. Определить полное перемещение свободного конца стержня и построить эпюру перемещений. Решение: Выбираем по таблице1 исходные данные согласно варианта:
На отдельной странице чертим расчетную схему с указанием исходных данных (Рис. 93, а). Из уравнения равновесия стержня определяем реакцию опоры стержня RA. Для этого проводим ось z в любую сторону и проектируем все внешние силы, действующие на стержень на ось z. откуда Минус показывает, что реакция опоры направлена в противоположную сторону. Зачеркиваем первоначальное направление реакции опоры и направляем ее в противоположную сторону. Указываем числовое значение реакции опоры. 4.Делим стержень на участки на участки. Границами участков являются точки приложения сосредоточенных сил, начало и конец приложения распределенных усилий и сечения, где изменяется площадь поперечного сечения стержня. Проводим через границы участков линии, перпендикулярные оси стержня. 5.Присваиваем номер каждому участку. Нумерацию участков следует вести со свободного конца стержня, чтобы не искать реакцию в заделке. Если реакция в заделке известна или определена с помощью уравнений равновесия, то нумерацию можно вести с любого конца стержня. Для нашей задачи нумерацию участков начнем со свободного конца стержня. 6.Методом сечений (правило РОЗУ) определяем продольную силу на каждом участке. Расчет продольных сил и нормальных напряжений сводим в таблицу 14. Таблица 14 - Расчет продольных сил и нормальных напряжений.
По полученным значениям строим эпюру продольных сил (Рис.93, б) и нормальных напряжений (Рис.93, в). 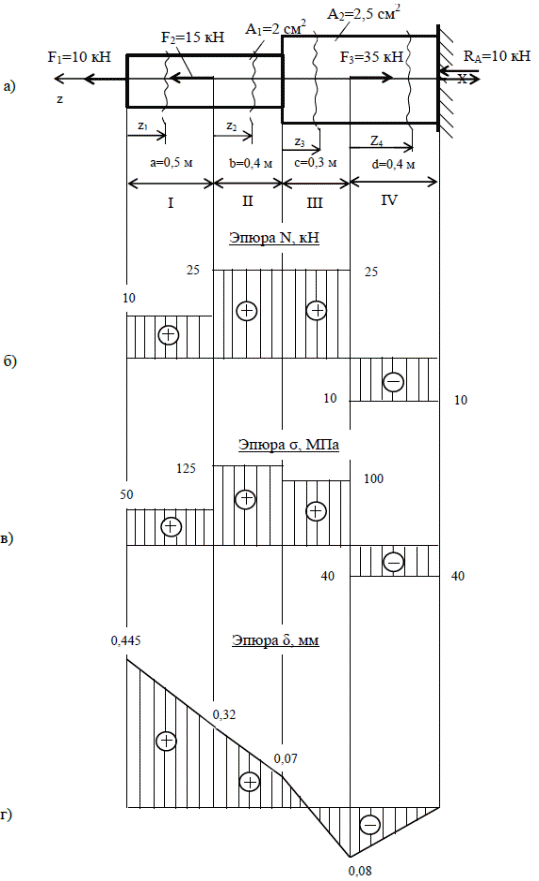 Рис.93 – Расчетная схема и эпюры продольных сил, нормальных напряжений и перемещений Определим коэффициент запаса прочности. Опасным участком является участок II, где действуют максимальные по величине напряжения. Нормальные напряжения на участке II, будут равны . Коэффициент запаса прочности определится: Для определения нормального и касательного напряжения в наклонном сечении рассечем стержень на участке II плоскостью под углом к поперечному сечению (Рис.94). 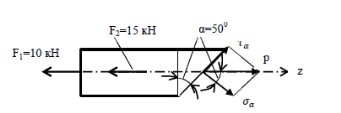 Рис.94 – Схема для определения напряжений в наклонном сечении Напряжения в наклонной площадке будут равны: Полное перемещение свободного конца стержня определится как алгебраическая сумма удлинений (укорочений) участков стержня. Определим абсолютные удлинения, укорочения участков стержня: Для построения эпюры перемещений выберем начало координат. Им является сечение заделки стержня. Тогда перемещение левого конца участка IV будет равно его укорочению: Перемещение левого конца участка III: Перемещение левого конца участка II: Полное перемещение свободного конца стержня Свободный конец стержня удлинится на 0,445 мм. Строим эпюру перемещений сечений стержня (Рис.93,г). Расчетно-графическое задание №2 Прежде чем приступить к решению задачи, следует изучить по учебнику материал, относящийся к статически неопределимым системам, работающим на растяжение (сжатие). Стержни, реакции опор у которых не могут быть определены из уравнений равновесия, называются статически неопределимыми. Для решения статически неопределимых стержней, кроме уравнений равновесия необходимо составить дополнительные уравнения совместности деформаций. Этих уравнений необходимо составить столько, сколько раз стержень статически неопределим. Величина статической неопределимости n определяется по разности количества неизвестных реакций опор R и количества независимых уравнений равновесия по формуле В этом будет состоять статическая сторона задачи. Геометрическая сторона задачи состоит в выборе основной системы. Для этого отбрасывается такое количество опор, чтобы стержень стал статически определимым. Отброшенные опоры заменяются реакциями. Полученный таким образом статически определяемый стержень и будет основной системой. Для того, чтобы она была эквивалентна заданному стержню по характеру деформирования, необходимо выполнение условий (перемещение под отброшенной опорой рано нулю, общее перемещение равно нулю). Физическая сторона задачи состоит в том, чтобы определить общее перемещение от действующей нагрузки и реакций связи и составить уравнение совместности деформаций, при котором перемещение будет равно нулю, из которого и определяются реакции опор. Задача № 2. Расчет статически неопределимого ступенчатого стержня. Для статически неопределимого стержня, нагруженного системой внешних сил определить: 1. Продольные силы и нормальные напряжения в поперечных сечениях ступенчатого стержня; 2. Построить эпюры продольных сил и нормальных напряжений; 3. Проверить условие прочности для опасного сечения стержня при [σ] =160 МПа; 4. Построить эпюру перемещений (Е = 2.105 МПа). Решение: Выбираем по таблице 2 исходные данные согласно варианта:
На отдельной странице чертим расчетную схему с указанием исходных данных (Рис. 95, а). Определяем степень статической неопределимости системы по формуле где так как неизвестны две реакции опоры и ; , потому что из трех уравнений равновесия для плоской системы сил стержня можно составить только одно уравнение равновесия: В результате получим что система один раз статически неопределима. Отбрасывая опору В и заменяя ее реакцией связи получаем основную систему, которая будет статически определима (Рис.95, б). Сечения стержня могут перемещаться. Решили геометрическую сторону задачи. Решение физической стороны задачи будет состоять в том, что деформация основной системы и расчетной схемы будут эквивалентны при условии, что общее удлинение стержня будет равно нулю, так как стержень зажат с двух сторон. Составляем уравнение совместности деформации: Применяя принцип независимости действия сил, найдем перемещение сечения В стержня отдельно от внешних сил и неизвестной реакции RВ. 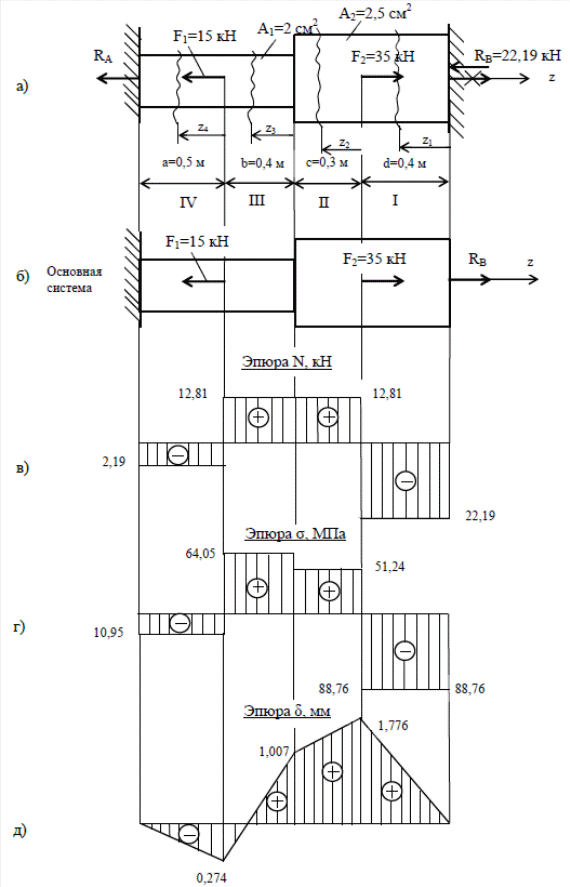 Рис.95 – Расчетная схема, основная система и эпюры продольных сил, нормальных напряжений и перемещений Прикладываем к основной системе реакцию опоры RВ и находим Прикладываем к основной системе внешнюю силу и находим Прикладываем к основной системе внешнюю силу и находим Уравнение совместности деформации запишется в виде: Минус показывает, что направление реакции опоры RВ нужно сменить на противоположное (Рис.95, а). Далее задача решается как статически определимая. Делим стержень на участки и присваиваем номер каждому участку. Методом сечений определяем продольную силу на каждом участке. Величину продольной силы и нормального напряжения сводим в таблицу 15. Таблица 15 - Расчет продольных сил и нормальных напряжений.
По полученным значениям строим эпюру продольных сил (Рис.95, в) и нормальных напряжений (Рис.95, г). Проверим прочность стержня. Для этого по эпюре нормальных напряжений определим опасный участок, это участок где действуют максимальные по величине напряжения. В нашем случае таким участком является участок номер 2, и его прочность будет обеспечена: Для построения эпюры перемещений возмем за начало координат левое сечение заделки А. Тогда перемещение правого конца участка IV будет равно его удлинению: Перемещение левого конца участка III: Перемещение левого конца участка II: Полное перемещение свободного конца стержня Строим эпюру перемещений сечений стержня (Рис.95, д). Эпюра перемещений является проверкой правильности решения задачи. Расчетно-графическое задание №3 Прежде чем приступить к решению задачи, следует изучить по учебнику материал, относящийся к теме напряженного состояния в точке, уяснить виды напряженного состояния, главные площадки и площадки сдвига, главные напряжения и экстремальные касательные напряжения, а также теорию чистого сдвига. Следует уточнить область практического применения сдвига при расчетах заклепочных, болтовых, шпоночных, шлицевых и других видов соединений на срез и смятие. При расчетах соединений на срез и смятие нужно четко представить, по каким площадкам действуют касательные напряжения среза и нормальные напряжения смятия. К этой теме относятся расчеты на прочность сварочных соединений. Задача № 3, а. Практические расчеты на срез и смятие. Для заданной схемы заклепочного соединения определить необходимое количество заклепок, для соединения листов внахлест, если 80 МПа, а Решение: Выбираем по таблице 3 исходные данные:
Чертим расчетную схему с указанием исходных данных (Рис. 96). 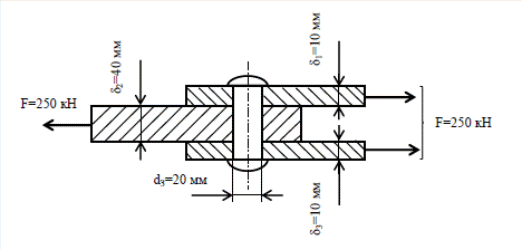 Рис.96 – Расчетная схема заклепочного соединения Заклепочное соединение одновременно должно удовлетворять условию прочности на срез и смятие, поэтому определяем количество заклепок n исходя из деформации среза: где – количество плоскостей среза. Из условия прочности на смятие: где – это минимальная толщина двух пластин , приходящихся на силу . Средняя толщина пластины Из двух расчетов выбираем большее значение и округляет до целого числа заклепок. Принимаем Задача № 3, б. Расчет сварочного соединения Для сварочного соединения, выполненного внахлест определить длину фланговых и лобового сварочных швов, если для сварных швов 100 МПа, а для материала пластины 160 МПа. Решение: Выбираем по таблице 3 исходные данные:
Чертим расчетную схему с указанием исходных данных (Рис. 97). 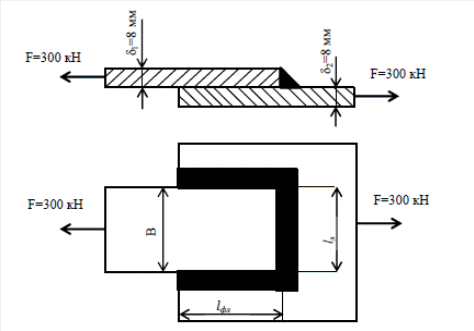 Рис.97 – Расчетная схема сварочного соединения Величина лобового сварочного шва равна ширине верхней пластины . Пластина испытывает деформацию растяжения. Из условия прочности пластины на растяжение определим длину лобового сварочного шва: Из условия прочности сварочного соединения выполненного внахлестку определим длину флангового сварочного шва: Расчетно-графическое задание №4 К решению задачи можно приступить после изучения тем «Сдвиг» и «Кручение». При кручении в поперечных сечениях бруса возникает только один внутренний силовой фактор - крутящий момент Мк. Крутящие моменты, возникающие в поперечных сечениях вала, определяются по внешним скручивающим Мск или вращающим Мвр моментам с помощью метода сечений. Крутящий момент Мк в любом поперечном сечении вала численно равен алгебраической сумме внешних скручивающих или вращающих моментов, приложенных по одну сторону от рассматриваемого сечения. Вал должен одновременно удовлетворять условиям прочности и жесткости: крутящий момент в опасном сечении вала, определяется по эпюре крутящих моментов; полярный момент сопротивления сечения: - для вала круглого поперечного сечения , где - диаметр вала; - для вала кольцевого поперечного сечения , где наружный диаметр вала; отношение внутреннего диаметра кольцевого вала к наружному; полярный момент инерции сечения . Угол поворота одного поперечного сечения вала относительно другого называется углом закручивания участка вала, величина которого определяется . Произведение модуля сдвига G на полярный момент инерции сечения называется жесткостью сечения. Угол положителен, если при взгляде относительно внешней нормали рассматриваемого сечения он направлен против часовой стрелки и отрицателен, если по часовой стрелке. Задача № 4. Расчет вала на кручение. Для заданного вала при =80 МПа, G=8·10 4 MПa, [ 1. Построить эпюру крутящих моментов. 2. Определить диаметр вала из условия прочности и жесткости на кручение. 3. Построить эпюру максимальных касательных напряжений. 4. Построить эпюру углов закручивания, производя отсчет углов от опорного защемления. 5. Из условия равнопрочности вала для опасного участка заменить круглое поперечное сечение вала кольцевым при α = 0,7 и сравнить вес вала. Решение: Выбираем по таблице 4 исходные данные: На отдельной странице чертим расчетную схему с указанием исходных данных согласно таблице (Рис. 98,а).
Направление скручивающих моментов на расчетной схеме определяем по знакам в 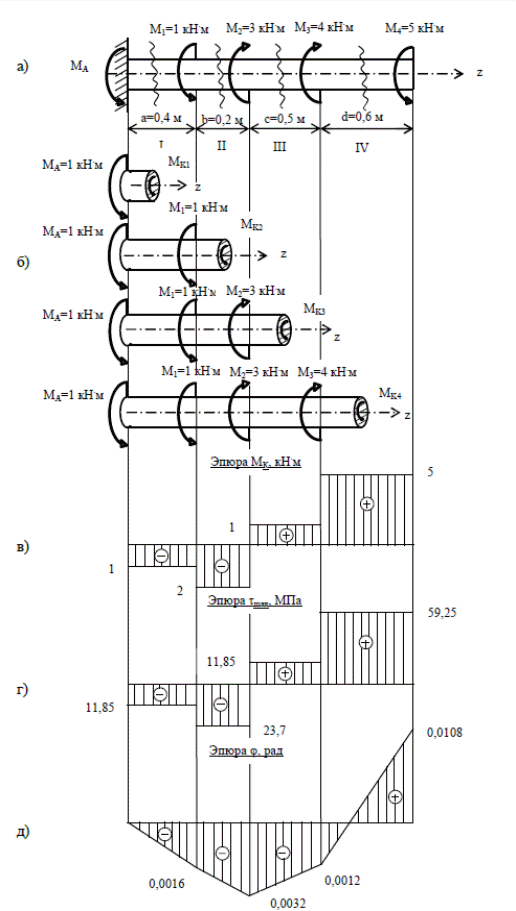 Рис.98 – Расчетная схема и эпюры вала при кручении Таблице исходных данных. Если стоит знак (+), то со стороны оси z момент направлен против направления движения часовой стрелки, если (–), то по часовой стрелке. Из уравнения равновесия вала определяем реактивный момент в сечении заделки вала МA. Для этого проводим ось z в любую сторону и проектируем все внешние скручивающие моменты, действующие относительно оси z. откуда Указываем числовое значение реактивного момента на расчетной схеме. 4. Делим вал на участки на участки. Границами участков являются сечения приложения скручивающих моментов, сечения, где изменяется площадь поперечного сечения вала. Проводим через границы участков линии, перпендикулярные оси вала. 5. Присваиваем номер каждому участку. Чтобы не искать реакцию в заделке нумерацию участков следует вести со свободного конца вала. Если реакция в заделке определена с помощью уравнений равновесия, то нумерацию можно вести с любого конца вала. Для нашей задачи нумерацию участков начнем с левого конца вала. 6. Методом сечений (правило РОЗУ) определяем крутящий момент на каждом участке. Уравнение равновесия оставшейся части вала определяем с поможью метода местных координат (рис.98, б). Расчет крутящих моментов сводим в таблицу 16. Таблица 16. Расчет крутящих моментов.
По полученным значениям строим эпюру крутящих моментов (Рис.98, в). По эпюре крутящих моментов определяем опасный участок. В нашем случае это участок IV, где действует максимальный крутящий момент 7. Определяем диаметр вала из условия прочности: откуда ; =72 мм. Определяем диаметр вала из условия жесткости: ; Откуда Из двух проектных расчетов выбираем больший диаметр вала и округляем до значения кратного пяти. Принимаем диаметр вала 8. Определим максимальные касательные напряжения на каждом участке. Результаты расчетов сводим в таблицу 17. Таблица 17. Расчет максимальных касательных напряжений.
По полученным значениям строим эпюру касательных напряжений на участках вала (Рис.58, г). 9. Определяем величину углов закручивания каждого участка. Результаты расчетов сводим в таблицу 18. Таблица 18 - Расчет углов закручивания.
Построение углов закручивания поперечных сечений вала начинаем от опорного защемления и учитываем, что угол закручивания последующего участка равен алгебраической сумме углов закручивания предыдущих участков (Рис.58, д). Для опасного участка IV заменим вал круглого поперечного сечения кольцевым из условия равнопрочности валов. Условие равнопрочности означает, что касательные напряжения, действующие на поверхности вала круглого и кольцевого поперечного сечения равны друг другу. Тогда имеем: или откуда наружный диаметр кольцевого вала равен: =0,082 м. Внутренний диаметр 0,057 м. Для сравнения веса разделим вес вала круглого поперечного сечения G на вес вала кольцевого поперечного сечения GК. С учетом того, что длина участка вала и плотность материала вала одинакова, отношение равно: Получили, что вал кольцевого сечения легче вала круглого поперечного сечения. Экономия металла в случае кольцевого вала составит 1,62 раза. Расчетно-графическое задание №5 К решению задачи следует приступить после изучения раздела«Геометрические характеристики плоских сечений». Размеры и форма поперечных сечений определяют значения таких геометрических характеристик как площадь поперечного сечения А, статический момент сечения SХ, SУ, осевые IХ, IУ, полярный Iρ, центробежный IХУ моменты инерции сечения, осевые моменты WX, WУ, полярный момент Wρ сопротивления сечения, радиусы инерции iX, iУ инерции сечения. Необходимо уяснить такие понятия как центр тяжести поперечного сечения, главные оси инерции и главные центральные оси инерции. Задача 5. Геометрические характеристики плоских сечений. Для составного поперечного сечения, изготовленного из стандартных прокатных профилей, требуется: 1. Определить положение центра тяжести относительно произвольных осей. 2. Построить центральные оси, параллельные выбранной произвольной системе осей, относительно которых определен центр тяжести сечения. 3. Определить величины осевых и центробежного момента инерции относительно центральных осей. 4. Определить положение главных центральных осей инерции. 5. Найти экстремальные значения осевых моментов инерции относительно главных центральных осей инерции. 6. Определить главные радиусы инерции и построить эллипс инерции. 7. Начертить сечение в масштабе и указать на нем все оси и все размеры. 8. При расчете все необходимые данные следует брать из таблиц сортамента. Решение: Выбираем по таблице 5 методических указаний исходные данные:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
