кристалл. Контрольная (семестровая) работа по дисциплине Кристаллография и кристаллохимия

• Название: Контрольная (семестровая) работа по дисциплине Кристаллография и кристаллохимия
• Дата: 18.12.2021
• Размер: 473.59 Kb.
• Имя файла: кристалл.docx
• Тип: Документы; #307990

Министерство высшего образования и науки РФ

ФГБОУ ВО «Волгоградский государственный технический университет»

Факультет технологии конструкционных материалов

Кафедра «Машины и технология литейного производства»

Контрольная (семестровая) работа по дисциплине

«Кристаллография и кристаллохимия»

Вариант № 12

Выполнил:

Студент гр. М-234

Давыденко А.Ю.

Проверил: преподаватель

Григорьева Н.В.

Волгоград 2021

Содержание

1. 
   Задание……………………………………………………………3
   
2. 
   Задание №1……………………………………………………….4
   
3. 
   Задание №2……………………………………………………….4
   
4. 
   Задание №3……………………………………………………….5
   
5. 
   Задание №4……………………………………………………….5
   
6. 
   Задание №5……………………………………………………….5
   
7. 
   Задание №6………………………………………..……...…….6-9
   

Задание:

1. 
   Сделать эскиз модели элементарной ячейки кристаллический структуры меди в осях координат и присвоить индексы узлам ячейки
   
2. 
   Определить индексы направлений, проходящих через указанные узлы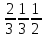
   

1 - [[ ]] [[001]];

2 - [[111]] и [[001]];

3. 
   Построить наглядное пространственное изображение направления в кубической ячейке [011]
   
4. 
   Определить символ плоскости, отсекающей на осях координат отрезки, заданные параметрами
   

а) а = ∞, в = 3, с = 3;

б) для (121) ОА = 12,75, ОВ = 6,34, ОС = 2,4;

для hkl ОА₁ = 4,25, ОВ₁ = 6,34, ОС₁ = 1,2;

5. 
   Найти hkil для плоскостей, заданных в 3-х осной системе координат XYZ (211);
   
6. 
   Определение углов между направлениями, плоскостями, прямой и плоскостью.
   

1.Сделать эскиз модели элементарной ячейки кристаллический структуры меди в осях координат и присвоить индексы узлам ячейки.

О 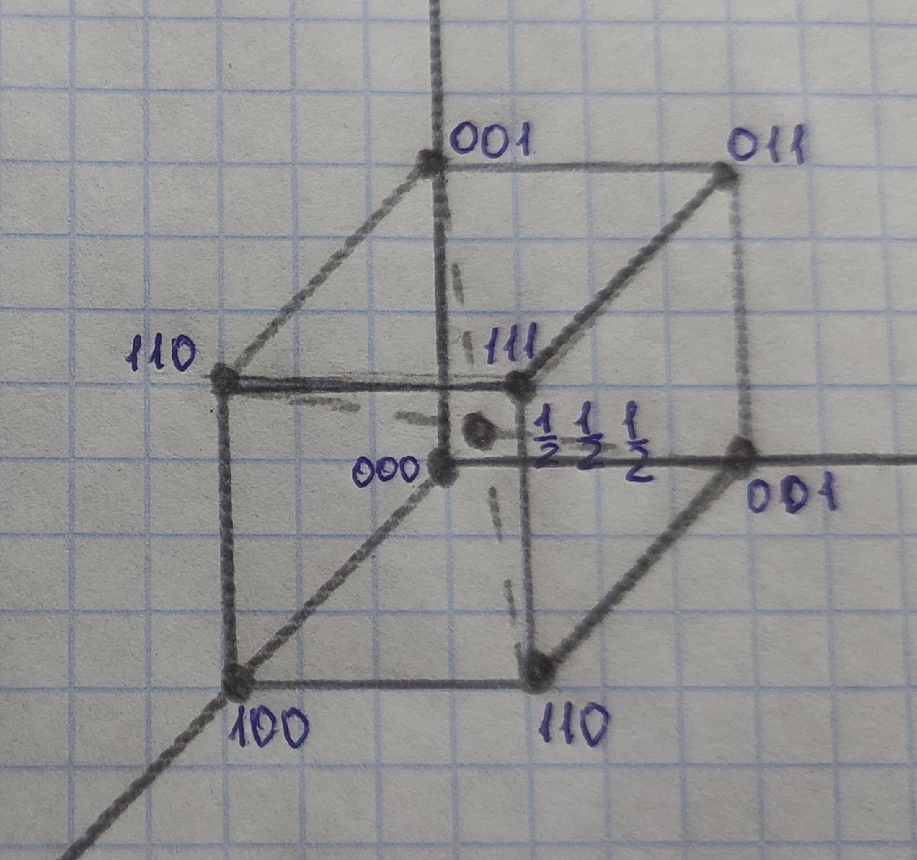ОЦК

2.Определить индексы направлений, проходящих через указанные узлы

M [[mnp]]

[u:v:w]=(m2-m1):(n2-n1):(p2-p1)

1 - [[2/3 1/3 1/2]] [[001]]= [[0-2/3 0-1/3 1-1/2]]=[[2/3 1/3 1/2]]

2. 
   - [[111]] и [[001]]=[[0-1 0-1 1-1]]= [[1 1 0]]
   

3.Построить наглядное пространственное изображение направления в кубической ячейке [011]

4.Определить символ плоскости, отсекающей на осях координат отрезки, заданные параметрами

а) а = ∞, в = 3, с = 3;

б) для (121) ОА = 12,75, ОВ = 6,34, ОС = 2,4;

для hkl ОА₁ = 4,25, ОВ₁ = 6,34, ОС₁ = 1,2;

(hkl)=1/a:1/b:1/c = (1/∞; 1/3; 1/3) = (0;1/3; 1/3)

ОА₁/ОА:ОВ₁/ОВ:ОС₁/ОС = 4,25/12,75:6.34/6,34:1,2/2,4 = 1/3:1:1/2=3:10:5

5.Найти hkil для плоскостей, заданных в 3-х осной системе координат XYZ (211);

hkl hkil h+k+l=0

(211)=(2131)

6.Определение углов между направлениями, плоскостями, прямой и плоскостью.

Межплоскостное расстояние. Между индексами (hkl)семейства параллельных плоскостей, его межплоскостным расстоянием и периодами решетки существует математическая связь. Формула, показывающая зависимость между этими величинами, получила название квадратичной формы.

Межплоскостное расстояние для решетки с произвольной сингонией:

(1.1)

где параметр определяется из формулы: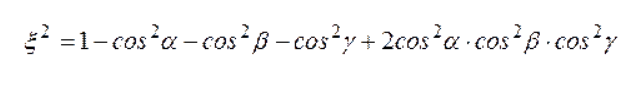

(1.2)

В частном случае формулы для межплоскостного расстояния имеют вид:

кубическая сингония:

(1.3)

тетрагональная сингония:

(1.4.)

гексагональная сингония: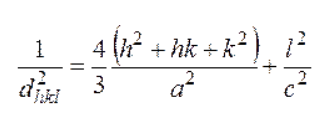

(1.5)

Из формул видно, что чем больше индексы плоскости, тем меньше межплоскостное расстояние для данного семейства плоскостей.

Семейства плоскостей с одинаковым межплоскостным расстоянием образуют совокупность плоскостей, обозначаемую фигурными скобками . Так, для кубической сингонии совокупность плоскостей куба {100} содержит шесть кристаллографически идентичных семейств плоскостей: (100), (010), (001), (100), (010), (001), связанных между собой преобразованиями симметрии. Если с помощью различных операций симметрии повернуть решетку так, что на месте плоскостей разместятся плоскости или любые из остальных четырех семейств плоскостей, то новое положение решетки совпадет с исходным. В этом и заключается кристаллографическая идентичность.

Количество кристаллографически идентичных плоскостей равно числу возможных перестановок местами и знаками индексов, входящих в данную совокупность, без изменения величины: межплоскостного расстояния. Кристаллографически идентичные плоскости симметрично расположены в пространстве.

Количество плоскостей в совокупности принято обозначать буквой Р. Так, в кубической сингонии для {100} Р = 6; для {110} Р = 12; {111} Р = 8; {123} Р = 24.

Угол между направлениями, сводится к определению угла между векторами и и вычислив величину этого скалярного произведения, найдем: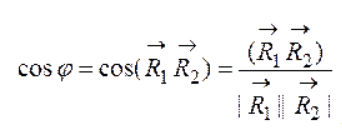



(1.6)

В общем виде формула для нахождения угла между двумя направлениями, выраженная через индексы направлений, является слишком громоздкой, поэтому ограничимся рядом частных случаев:

кубическая сингония: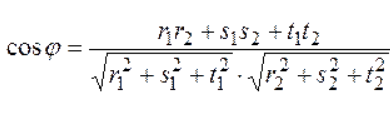

(1.7)

тетрагональная сингония:

(1.8)

Угол между плоскостями.

кубическая сингония: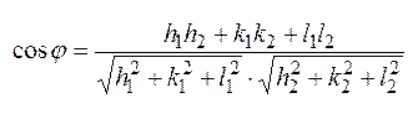

(1.9)

тетрагональная сингония: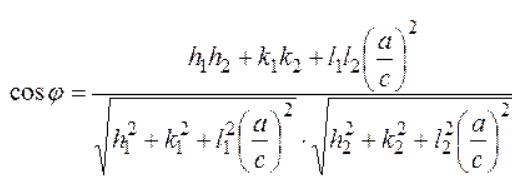

(1.10)

Объем элементарной ячейки. Если известны параметры ячейки (длины ребер и углы), можно определить ее объем по формуле: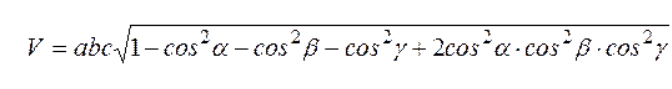

(1.11)

где V – объем; a, b, c – параметры ячейки; a, b, g - углы.

В символах узлов могут применяться и дробные индексы; для символов направлений и плоскостей (ребер и граней) используются только целочисленные индексы.