|
|
кр 7 алг. КР алг 7. Контрольные работы к 1
РАЗДЕЛ III
Контрольные работы
К— 1 Вариант I
Разложите на простые множители число: а) 388; б) 2520.
Представьте в виде десятичной дроби число:
а) 3 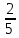 ; б) ; б) 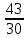
Сравните числа: 0,3; 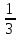 ; 0,(32); 0,(322). Выбрав единичный отрезок, укажите расположение данных чисел на координатной оси. ; 0,(32); 0,(322). Выбрав единичный отрезок, укажите расположение данных чисел на координатной оси.
Вычислите:
а) (1,075 – 0,05): 0,25; б) 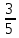 : : 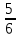 + 2 + 2 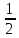 · · 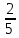 – 1: l – 1: l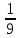 ; ;
в) (–2)3 + (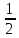 )2 – 24. )2 – 24.
К— 1 Вариант II
Разложите на простые множители число: а) 376; б) 2640.
Представьте в виде десятичной дроби число:
а) 3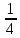 ; б) ; б) 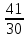 . .
Сравните числа: 0,6; 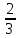 ; 0,(67); 0,(677). Выбрав единич- ; 0,(67); 0,(677). Выбрав единич-
ный отрезок, укажите расположение данных чисел на координатной оси.
Вычислите:
а) (1,225 + 0,05): 0,25; б) 1: l 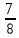 + + 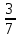 · · 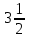 - - 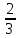 : : 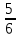 ; ;
в) (–3)2 + 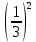 ·33. ·33.
К— 1 Вариант III
Разложите на простые множители число: а) 4680; б) 16 830; в) 14 641.
Представьте в виде десятичной дроби число:
а) 2±; б) Ц.
Представьте в виде обыкновенной дроби число: а) 0,(7); б) 0,(17);
в) 0,(045); г) 3,6(17).
Вычислите:
а) 2,2(7) + 4^ • (0,625 - 1,64 : 1,6);
б) (0,5)20 • 221 + З7 • 57 : 156.
Сколько делителей имеет число 140?
К—1 Вариант IV
Разложите на простые множители число: а) 7020; б) 17 680; в) 28 561.
Представьте в виде десятичной дроби число: a) 3i; б) «.
Представьте в виде обыкновенной дроби число:
а) 0,(8); б) 0,(43);
в) 0,(027); г) 5,2(18).
Вычислите:
а) (0,75 - 0,25 • 4,2): 0,2(45) +
б) (0,2)20 • 521 + 26 • 56 : 105.
Сколько делителей имеет число 150?
К—2 Вариант I
Запишите одночлен в стандартном виде:
а) 3а2bс • 6abc;
Запишите многочлен в стандартном виде:
а) а – 7а; б) 7а + b2 –3а – 2b2; в) 3х – (2а – х).
Вынесите за скобки общий множитель многочлена:
а) 12x– 6у; б)2аb – 6bс; в) 9x2 –12х2у3.
Преобразуйте выражение в многочлен стандартного вида:
а) 2x 2(x – 3у);б) (2x – 3у)(3у + 2x);
в) (а + b)(a – b)(a + b).
Разложите на множители:
а) т(п – 3) + 2(п – 3);
б) х – 2у – а(2у – х).
К—2 Вариант II
Запишите одночлен в стандартном виде:
а) 4а3bс · 3аb2с;
б) (–2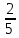 )b3c2 · (– )b3c2 · (– 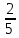 )b2c2. )b2c2.
Запишите многочлен в стандартном виде:
а) b – 8b; б) 15х + 3у2 - 8х + 3у2;
в) 14b-(3a-7b).
Вынесите за скобки общий множитель многочлена:
а) 15а + 3b; б) 14ху - 28ау; в) 20а5b3-15b4.
Преобразуйте выражение в многочлен стандартного вида:
а) 3а(2 – b); б) (5а – 6b)(6b - 5а); в)(х – у)(х + у)(х – у).
Разложите на множители:
а) а(5 – b) + 7(5 – b);
б) 7а – 4b – у(4b – 7а).
К—2 Вариант III
Запишите одночлен в стандартном виде:
а) -4,5a3bcl,2ab2c3;
б) (_3| у с2 • {^)Ъ2с3.
Упростите выражение
(х - 1)(х - 3)(х + 4)-(х+ 1)(х + 3)(х - 4).
Преобразуйте выражение в многочлен стандартного вида:
а) (х2 - 3у)(3у + х2); б) (а2 - b2)(b4 + a2b2 + а4).
Разложите на множители:
а) \2х2у - 18ху2; б) 15а4Ь3 - 25а3Ь4;
в) тпп - 3m + 2п - 6; г) х2 - ху - 2у2.
Докажите тождество
(х - 1)(х + 1)(JC2 + 1)(х4 + 1) = х8-1.
К—2 Вариант IV
1. Запишите одночлен в стандартном виде:
а) -Зг5аЬ3с2 • 1,6а3£>с;
б) (_2|]b4c2 •
Упростите выражение
(х - 1)(х - 2)(х 4- 3) - (х + 1)(х + 2)(х - 3).
Преобразуйте выражение в многочлен стандартного вида:
а) (2Ъ 4 а3)(а3 - 2Ь); б) (х2 + у2)(у4 - х2у2 4- х4).
Разложите на множители:
а) 16аЬ3 - 20а2Ь2; б) 18х4у2 - \2хьи3;
в) ттг - 2т 4- 4д - 8; г) х2 4- 3 ху - 4 у.
Докажите тождество
(х - 1)(х7 + X6 + X5 + X4 + X3 + X2 + X + 1) = X8 - 1.
К—3 Вариант I
Преобразуйте выражение в многочлен стандартного вида:
а) (х – 3)2; б) (2а + 5b)2;
в) (а – 2)(а + 2); г) (3х – у)(у + 3х).
Разложите на множители:
а) 18ab3 – 2а3b; б) а4 + 6а2b + 9b2.
Преобразуйте выражение в многочлен стандартного вида:
2(5 – у2)(у2 + 5) + (у2 – 3)2 – (у2 + у – 1)(4 – у2).
К—3 Вариант II
Преобразуйте выражение в многочлен стандартного вида:
а) (п – 2)2; б) (2а + 3b)2;
в) (х – 5)(х + 5); г) (4х – у)(у + 4х).
Разложите на множители:
а) (а + 3b)2 - (3а – b)2; б) а – b2 – b + а2.
Преобразуйте выражение в многочлен стандартного вида:
3(2 – х)2 – (2х2 + х – 5)(х2 – 2) + (х2 + 4)(4 – х2).
К—3 Вариант III
1. Преобразуйте выражение в многочлен стандартного вида:
а) (х2 - Зу)2; б) [2az + \&)>
в) (х2 - 2у)(х2 + 2у); г) (Зх - у)(у 4- Зх).
Разложите на множители:
а) (За2 + 2Ъ)2 - (За2 - Ь)2; б) 0,25а4 - За262 + 9Ъ4; в) х2 - 6х + 5; г) х2 + 4ху - 5у2.
Преобразуйте выражение в многочлен стандартного вида:
4(4 - у2)(у2 + 4) - (5 - у3)2 + (у4 + 4у2 + 16)(у2 - 4).
Вычислите значение выражения при каждом значении х:
в многочлен стандартного
б) (за3 + !&2)2; г) {2х2-Ъ){2х* + Ь\
б) 1а4 + 2а262 + 4Ь4; г) х2 + 6ху + 8у2.
(х - 1)(х - 2)(х + 3) - (х + 1)(х + 2)(х - 3).
К—3 Вариант IV
Преобразуйте выражение вида:
а) (п2 - 2т)2;
в) (х3 - 2у)(х3 + 2у);
Разложите на множители: а) (2а3 - 3Ъ2)2 - (2а3 + Ъ2)2; в) х2 - 5х + 4;
Преобразуйте выражение в многочлен стандартного вида:
3(3 - х2)2 - (9 - Зх2 + х4)(х2 + 3) - 3(х2 - х)(х2 + х).
Вычислите значение выражения при каждом значении х:
(х - 1)(х - 3)(х + 4) - (х + 1)(х + 3)(х - 4).
К—4 Вариант I
Сократите дробь:
a) б) 15а2-ЮаЬ
8 Ъ2-
|
12 аЪ
|
1
|
1
|
а- 1
|
а + 1'
|
7т2п
|
. 21т
|
8х ' 20х2у '
24х у
|
|
|
 Скачать 87.95 Kb.
Скачать 87.95 Kb.