Хомич В.А. - Основы химической термодинамики (2009) (1). Контрольные вопросы для самопроверки знаний по разделу дисциплины физической химии Химическая термодинамика
 Скачать 0.87 Mb.
|
Пример. Рассмотрим реакцию протекающую при р = const.C(графит) + O2(газ) → CO2(газ); тепловой эффект реакции равен ∆H1. Запишем реакцию через промежуточные стадии. C(графит) + 0,5O2(газ) = CO(газ) , ∆H2 ; (3.1) CO(газ) + 0,5O2(газ) = CO2(газ) , ∆H3; (3.2) Просуммируем реакции (3.1) и (3.2): C(графит) + O2(газ) → CO2(газ). Получаем исходную реакцию; поэтому сумма тепловых эффектов реакций (3.1) и (3.2) равна тепловому эффекту исходной реакции: ∆H2 + ∆H3 = ∆H1. Условие применения закона Гесса: закон применим только к тепловым эффектам процесса , т.е. к условиям, когда процесс протекает при р = const или V = const. Закон применим не только к химическим реакциям, но и к любым другим физико-химическим процессам. Пример: ∆Hвозгонки = ∆Hплав. + ∆Hиспар. 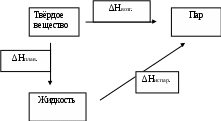 Термодинамическое обоснование закона Гесса заключается в следующем. Установлено, что QV = ∆U, а QP = ∆Н. Так как внутренняя энергия Uи энтальпия Hявляются функциями состояния системы, т. е. не зависят от пути процесса, то QV и QP не будут зависеть от промежуточных стадий, а определяются только начальным и конечным состоянием системы. Практическое значение закона Гесса заключается в следующем. Закон позволяет рассчитывать тепловые эффекты процессов не проводя экспериментов; тепловые эффекты неосуществимых процессов и процессов, для которых тепловой эффект нельзя определить опытным путём. Уравнение химической реакции с указанием теплового эффекта называется термохимическим уравнением. С термохимическими уравнениями можно обращаться так же, как и с алгебраическими уравнениями (складывать, умножать, делить). Первое следствие из закона Гесса: тепловой эффект обратной реакции равен по величине и противоположен по знаку тепловому эффекту прямой реакции.   .Второе следствие из закона Гесса: тепловой эффект реакции равен сумме теплот (энтальпий) образования продуктов реакций за вычетом (минус) суммы теплот (энтальпий) образования исходных веществ.  (3.3) здесь индекс f от лат. foramentum – образование.Например, для реакции aA + bB→cC + dD, ∆Hº298 = (с∆Hºf,298 (C) + d∆Hºf,298 (D)) – (a∆Hºf,298(A) + b∆Hºf,298(B)). При суммировании обязательно учитываются стехиометрические коэффициенты уравнения реакции. Для расчета тепловых эффектов используются стандартные теплоты образования веществ. Стандартной теплотой (энтальпией) образования вещества (  или  ) называетсяизменение энтальпии при образовании одного моль вещества из простых веществ, находящихся при стандартных условиях. Стандартная энтальпия простого вещества равна нулю.Например, если вещество получено по реакции выраженной термохимическим уравнением Ca(тв.) + C(графит) + 1,5O2(газ) = CaCO3(тв.) + 1207,7 Дж/моль, его стандартная теплота образования равна ∆Hºf,298(CaCO3)= - 1207,7 Дж/моль. Третье следствие из закона Гесса: тепловой эффект реакцииравен сумме теплот сгорания исходных веществ за вычетом (минус) суммы теплот сгорания продуктов реакции.  (3.4)здесь индекс с от лат. combustum - сгорание. Например, для реакции aA + bB→cC + dD, ∆H298 = a∆Hºс,298(A) + b∆Hºс,298(B) - c∆Hºс,298(C) - d∆Hºс,298(D) . Стандартная теплота сгорания вещества (∆Hºс,298 , ∆Hºсгор. ) – это убыль энтальпии в реакции сгорания одного моль простого вещества или соединения до соответствующих окисленных форм элементов. В случае сгорания соединений, состоящих из углерода и водорода (например, топливо) до CO2 и H2O. Стандартные теплоты сгорания и образования приведены в справочных таблицах термодинамических величин. Закон Кирхгофа устанавливает зависимость теплового эффекта реакции от температуры. Формулировка закона: температурный коэффициент теплового эффекта реакции равен изменению теплоемкости в результате процесса. Уравнение Кирхгофа для изобарного процесса (р = const):  , (3.5)где  .В зависимости от знака ∆Cр тепловой эффект реакции (процесса) с ростом температуры может увеличиваться или уменьшаться. Если ∆Cp> 0, то с ростом температуры ∆H увеличивается. Если ∆Cp< 0, то с ростом температуры ∆H уменьшается. Если ∆Cp = 0, то тепловой эффект не зависит от температуры. Проинтегрируем уравнение Кирхгоффа d∆H = ∆CрdT. Пусть теплоемкость Ср не зависит от температуры, т.е. ∆Ср = const, что допустимо в небольшом интервале температур. 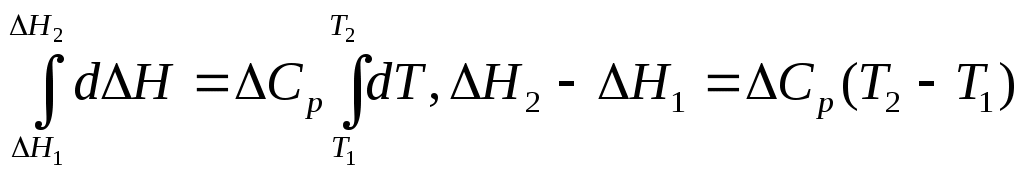 . Отсюда выведем формулу для вычисления теплового эффекта: ∆H2 = ∆H1 + ∆Cр(T2 – T1) . (3.6) 2. Пусть теплоемкость ∆Cр – является функцией от температуры, т.е. ∆Cp= f(T). Эта зависимость выражается уравнениями: Cp = a + bT + cT² или Cp = a + bT +  . В общем виде изменение теплоемкости равно ∆Cp = ∆a + ∆bT + ∆cT² + . (3.7)Подставим это выражение в уравнение Кирхгофа, тогда d∆HТ = (∆a + ∆bT + ∆cT² +∆  )dT.Возьмем неопределённый интеграл и получим выражение  . (3.8)Уравнение (3.8) показывает зависимость теплового эффекта реакции от температуры. В нем ∆H0 – постоянная интегрирования, определяемая как значение теплового эффекта при одной из температур. Уравнение Кирхгофа для изохорного процесса (V = const):  (3.9)Задача. Выразить зависимость теплового эффекта реакции от температуры, если известен тепловой эффект этой реакции при Т = 298 К и уравнение зависимости  . Данные термодинамических величин приведены в справочнике.Реакция : 2СН4 + СО2 = СН3СОСН3(г) + Н2О(г) протекает при 500 К. Решение. В основе решения – развернутое уравнение Кирхгофа (3.7):  .Для определения  и  надо знать зависимость для каждого из исходных веществ и продуктов реакции:  или  .Для нахождения постоянной интегрирования надо знать тепловой эффект реакции при температуре 298:  .Порядок расчета. 1. Данные из справочника заносим в таблицу. Таблица 2 Термохимические величины веществ
2. Находим тепловой эффект реакции при Т = 298 К.  3. Находим  в общем виде. .Принимает Т = 0.  .4. Находим 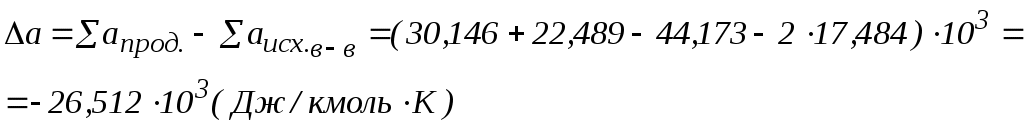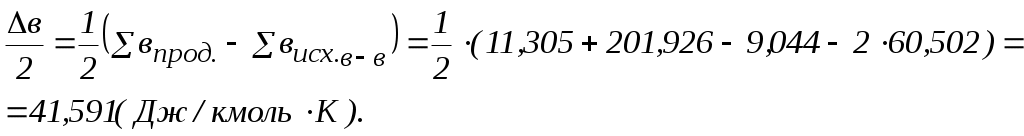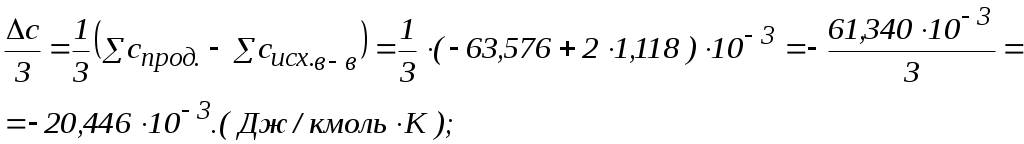и  .    .5. Вычисляем 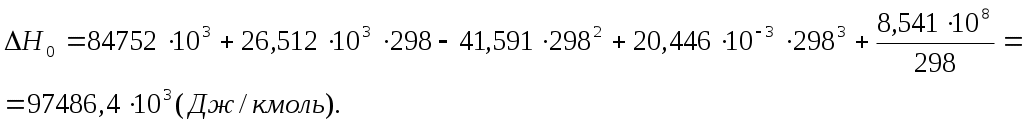  6. Находим теоретическую зависимость теплового эффекта реакции от температуры  7. Определим тепловой эффект при Т = 500 К. 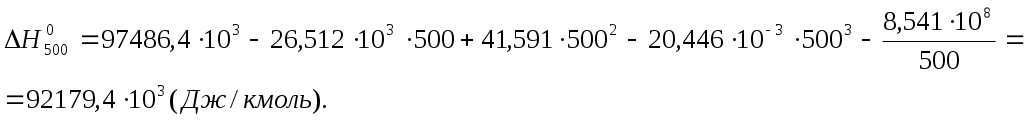 8. Определим насколько при температуре Т отличается  . где  - число кмоль продуктов реакции минус число кмоль исходных веществ в газообразном состоянии;  Л е к ц и я 4 ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ План лекции: Самопроизвольные (спонтанные) и несамопроизвольные процессы. Второй закон термодинамики, его формулировки. Аналитическое выражение второго закона термодинамики и его обоснование с использованием цикла Карно. Энтропия. Объединенное уравнение первого и второго законов термодинамики. Расчет изменения энтропии в простейших термодинамических процессах - изотермическом, изохорическом, изобарическом и адиабатическом. Постулат Планка. Изменение энтропии при фазовых переходах и при нагревании вещества. Абсолютное значение энтропии. Использование энтропии для определения направления протекания самопроизвольных процессов в изолированных системах. Самопроизвольные (спонтанные) процессы описываются следующими характеристиками. Все природные самопроизвольные процессы протекают в одном направлении, т. е. имеют одностороннее направление. Например, тепло от горячего тела переходит к холодному; газы стремятся занять наибольший объём. Часть энергии переходит в теплоту, т. е. система из упорядоченного состояния переходит в состояние с беспорядочным тепловым движением частиц. Самопроизвольные процессы можно использовать для получения полезной работы. По мере превращения система теряет способность производить работу. В конечном состоянии равновесия она имеет наименьший запас энергии. Систему нельзя вернуть в исходное состояние, не производя каких-либо изменений в ней самой или в окружающей среде. Все самопроизвольные процессы термодинамически необратимы. В самопроизвольном процессе начальное состояние является менее вероятным по сравнению с каждым последующим и наименее вероятным по сравнению с конечным. Несамопроизвольные процессы протекают при затрате работы; при этом система удаляется от состояния равновесия (например, сжатие газа, электролиз). Второй закон термодинамики– это постулат. Он имеет статистический характер и применим к системам из большого числа частиц. Второй закон термодинамики имеет следующие формулировки. Теплота не может переходить самопроизвольно от менее нагретого тела к более нагретому. Невозможен процесс, единственным результатом которого является превращение теплоты в работу. Вечный двигатель второго рода невозможен. Теплота, наиболее холодного из участвующих в процессе тел, не может служить источником работы. Аналитическое выражение второго закона термодинамики и его обоснование с использованием цикла Карно. Суть выражения второго закона термодинамики – связь самопроизвольности процесса с ростом энтропии.Это выражение вытекает из рассмотрения вопроса о теоретической полноте превращения теплоты в работу в обратимом цикле Карно. Цикл состоит из четырех процессов (рис.1): АВ – изотермическое расширение за счет теплоты Q1, подведенной к газу при температуре Т1; ВС – адиабатическое расширение; СД – изотермическое сжатие при температуре Т2, в этом процессе газ теряет теплоту Q2; ДА – адиабатическое сжатие до исходного состояния. 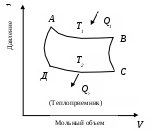 (Теплоотдатчик) Рис 1. Схема цикла Карно Теплота, поглощаемая (или выделяемая) при изотермическом расширении (или сжатии) одного моль идеального газа, равна работе  . (4.1)При адиабатическом расширении (или сжатии)  . (4.2)Применение этих уравнений к соответствующим процессам цикла приводит к выражению для термодинамического коэффициента полезного действия (к.п.д.):  . (4.3)Уравнение (4.3) является математическим выражением второго закона термодинамики. Так как T1 ‹ T2, то η ‹ 1. Согласно теории Карно замена идеального газа любым другим веществом не приведет к изменению к.п.д. цикла Карно. Замена цикла Карно любым другим циклом приведет к меньшему к.п.д. (теорема Клазиуса-Карно). Таким образом, даже в случае идеальной тепловой машины превращение теплоты в работу не может быть полным. Выражение второго закона термодинамики позволяет ввести понятие энтропии, с помощью которой сущность закона раскрывается в удобной и общей форме. Изменим выражение (4.3):  на  . (4.4)Отношение  называется приведенной теплотой. Уравнение (4.4) показывает, что алгебраическая сумма приведенных теплот по обратимому циклу Карно равна нулю.Для бесконечно малого обратимого цикла Карно  где  - элементарная приведенная теплота.Любой цикл может быть заменен совокупностью бесконечно малых циклов Карно:  . В пределе  эта сумма превратится в  .В теории интегралов доказывается, что если интеграл по замкнутому контуру равен нулю, то подинтегральное выражение есть полный дифференциал некоторой функции от параметров, определяющих состояние системы.  ,где S– это энтропия, такая функция состояния системы, полный дифференциал которой в обратимом процессе равен отношению бесконечно малого количества теплоты к температуре. Понятие «энтропия» введено Клаузиусом (1850). Это выражение является математическим выражением второго закона термодинамики для обратимых процессов. Изменение энтропии в обратимом процессе равно изменению энтропии в необратимом процессе, т.е.  . Сравним теплоты обратимого и необратимого процессов. Согласно первому закону термодинамики  . Внутренняя энергия U – это функция состояния системы, поэтому  . Максимальная работа совершается при обратимом процессе, поэтому  В общем случае для обратимого и необратимого процессов второй закон термодинамики имеет следующее математическое выражение:  . (4.5)Здесь dS = const, а изменяется только правая часть уравнения, т.е. значение величины теплоты. Единицы измерения энтропии: [S] = Дж/моль·К. Объединенное уравнение первого и второго закона термодинамики:  (4.6)Расчет изменения энтропии идеального газа. Выразим изменение внутренней энергии  Разделив уравнение (4.6) на Т , определим изменение энтропии:  (4.7)Из уравнения идеального газа:  следует, что  . Тогда, после подстановки этого соотношения в (4.7):  (4.8) Проинтегрируем выражение (4.8) при  и получим уравнение для расчета изменения энтропии идеального газа: (4.9)Изотермический процесс,  :  , (4.10)так как  , то  . (4.11)Изохорический процесс,  :  . (4.12)Изобарический процесс,  :  . (4.13)Адиабатический процесс,  :  . (4.14)Постулат Планкаимеет следующую формулировку: при абсолютном нуле энтропия правильно образованных кристаллов чистых веществ равна нулю. Постулат позволяет рассчитать абсолютное значение энтропии, если известны теплоты фазовых переходов, и если известны теплоёмкости вещества в различных агрегатных состояниях. Рассмотрим вычисление изменения энтропии в различных процессах. 1. Изменение энтропии  при фазовых переходах (T = const) определяется по формуле  , (4.15)где ∆H- теплота фазового перехода (кипение, испарение, возгонка, плавление); n – число моль вещества, переходящего из одной фазы в другую; n = g/M, где g – масса вещества, M – его молярная масса. 2. Изменение энтропии ∆S при нагревании. а) Пусть p = const, тогда  ,  . (4.16) Если Cр = const, тогда ∆S = Cр ln  , (4.17)где Т1 и Т2 – температуры начала и окончания нагревания вещества. Пусть Cр выражается в Дж/моль· К, тогда ∆S = nCрln , (4.18)Пусть Cpвыражается в Дж/г ·К, тогда ∆S = gCрln . (4.19)Если Cp зависит от температуры, т.е. Cр = f (T), тогда 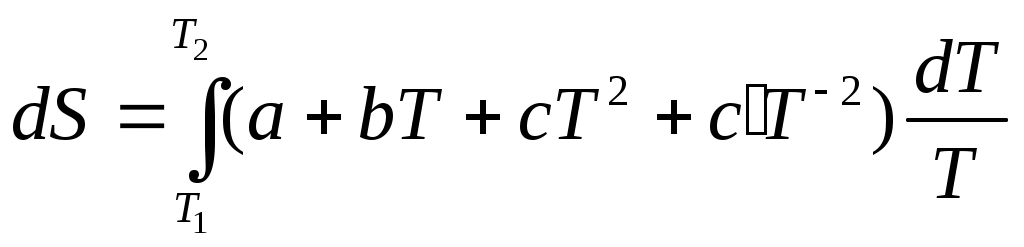 . (4.20)б) Пусть V = const, тогда  . (4.21)Для расчёта абсолютного значения энтропии S вещество нагревается от абсолютного нуля до данной температуры (p = const). Для твёрдого тела при температуре T  . (4.22)Для жидкости при температуре T 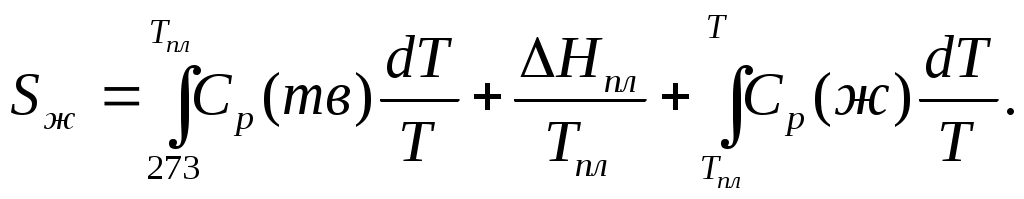 (4.23)Для газа при температуре T 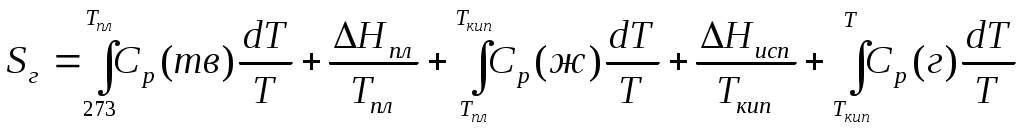 (4.24)Задача. Найти изменение энтропии g кг воды (тв.) Н2О при нагревании (охлаждении) в интервале температур от Т1до Т2, если известны температуры плавления и кипения, средние теплоемкости, теплоты плавления и испарения. Таблица 3 Термодинамические величины веществ
Решение. 1) Представим процесс нагревания вещества от Т1 и Т2по стадиям: 1 стадия. Твердое вещество (при Т1)  нагревание 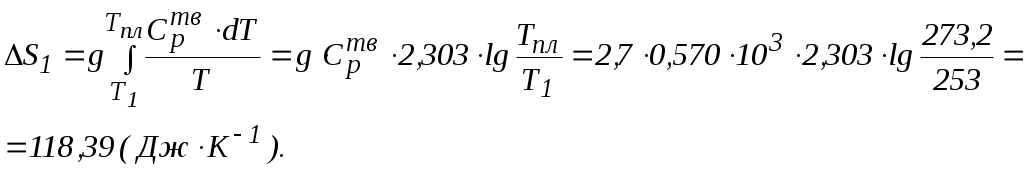 2 стадия. Твердое вещество (при Тпл.)   .3 стадия. Жидкость (при Тпл.)  нагревание 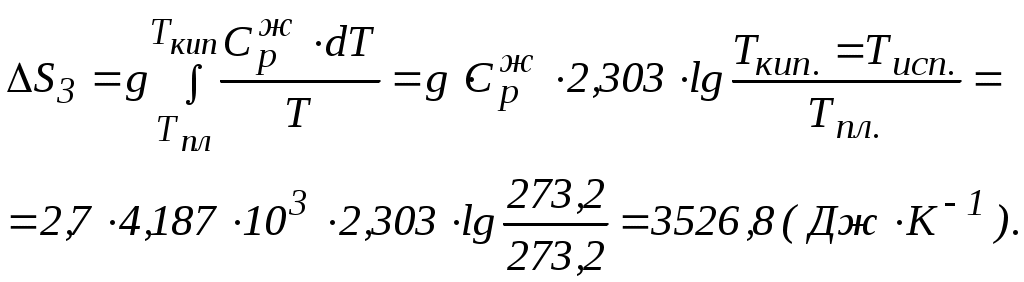 4 стадия. Жидкость (при Ткип.)  кипение  5 стадия. Пар (при Ткип.)  Пар (при Т2)нагревание 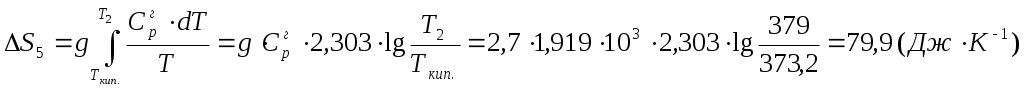 Находим изменение энтропии при нагревании вещества от Т 1 до Т2.  .Изменение стандартной энтропии системы  при протекании химической реакции определяется как разность суммы стандартных энтропий продуктов и суммы стандартных энтропий исходных веществ. (4.25)Значения величин стандартных энтропий (определенных для стандартных условий) веществ приведены в справочниках. Энтропия, как критерий возможности протекания процесса в изолированной системе (U,V = const). Изолированная система не обменивается с окружающей средой теплотой, т.е.  . Поэтому, согласно второго закона термодинамики (dS)U,V ≥ 0. (4.26) Необратимый процесс в изолированной системе возможен при (dS)U,V > 0. (4.27) При равновесном состоянии системы (или обратимом процессе) (dS)U,V = 0; (4.28) при этом энтропия принимает максимальное значение S = Smax. Если (dS)U,V < 0 (4.29) – необратимый процесс в изолированной системе неосуществим. Л е к ц и я 5 ТЕРМОДИНАМИКА АГРЕГАТНЫХ ПРЕВРАЩЕНИЙ План лекции: Уравнение Клайперона – Клаузиуса. Применение уравнения Клайперона – Клаузиуса к процессам испарения и возгонки. Зависимость давления насыщенного пара от температуры. Фазовые переходы чистого вещества в двухфазной однокомпонентной системе представим следующим образом.
При равновесии  или  .При этом  (5.1) (5.2)где  - это мольные объемы вещества в фазах α и β, - это энтропии вещества в фазах α и β.Так как  , получаем  Объединяем объемы и энтропии:  (5.3)Отсюда  (5.4)где  - это изменение энтропии при фазовом переходе; - это изменение объема при фазовом переходе.Так как  получаем  , (5.5)где  - изменение давления насыщенного пара с температурой.Уравнение (5.5) - это уравнение Клаузиуса-Клайперона, Применение уравнения Клаузиуса-Клайперона к процессам испарения и возгонки. «Жидкость  пар» или «твердое пар». или  . или  .Объемом конденсированного состояния (жидкости, твердого) можно пренебречь по сравнению с объемом пара и считать:  . Предложим, что пар подчиняется законам идеального газа, тогда  Подставляем это выражение в уравнение (5.5): , получаем:  Так как  , получаем  . (5.6)Это уравнение Клаузиуса-Клайперона для процессов испарения и выгонки. Физический смысл уравнения: с ростом температуры давление насыщенного пара в системе растет. При  можно из уравнения Клаузиуса-Клайперона найти значение величины теплового эффекта и равновесного давления насыщенного пара. Преобразуем уравнение (5.6), получаем  (5.7)Берем неопределенный интеграл выражения (5.7), после интегрирования:  (5.8)Уравнение (5.8) отвечает уравнению прямой линии. Построим графическую зависимость 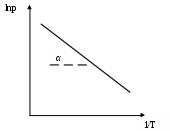 , рис. 2. Из графика находим тангенс угла наклона α:  , тогда  . Рис. 2. Графическая зависимость Возьмем определенный интеграл выражения (5.7), получаем:  . (5.9)Л е к ц и я 6 ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ План лекции: Термодинамический потенциал. Изохорно-изотермический потенциал или свободная энергия Гельмгольца. Применение энергии Гельмгольца в качестве критерия направления самопроизвольного процесса и равновесия в закрытых системах. Изобарно-изотермический потенциал или свободная энергия Гиббса. Применение энергии Гиббса в качестве критерия направления самопроизвольного процесса и равновесия в закрытых системах. Характеристические функции: внутренняя энергия, энтальпия, свободная энергия Гельмгольца, свободная энергия Гиббса. Уравнения Гиббса-Гельмгольца. Химический потенциал. Термодинамический потенциал – это функция состояния системы, убыль которой в процессе, протекающем при постоянстве двух параметров, равна максимальной полезной работе. Энергия Гельмгольца как изохорно-изотермический потенциал. Для изохорно-изотермических условий V = const, T = const. Вспомним, что объединенное уравнение, выражающее первый и второй законы термодинамики, имеет следующий вид:  . Так как при V = const,  = 0, получим  . (6.1) Проинтегрируем данное уравнение:   .Введем обозначение F – это энергия Гельмгольца. F = U - TS (6.2) Тогда F2 = U2 - TS2и F1 = U1 - TS1.  ,  или  То есть энергия Гельмгольца – это термодинамический потенциал, так как его изменение равно полезной работе при протекании обратимого процесса в системе. Для необратимого процесса:  В общем случае для обратимого и необратимого процессов справедливо выражение  (6.3)Энергия Гельмгольца равна  , отсюда U = F+TS. (6.4) То есть F – это та часть внутренней энергии, которая может быть превращена в работу, поэтому она называется свободной энергией; произведение TS – это энергия, которая выделяется в виде тепла, поэтому она называется связанной энергией. Энергия Гельмгольца как критерий возможности протекания процесса. Дифференцируя выражение получим dF = dU – TdS - SdT . Подставляя вместо произведения TdS его выражение из «объединенного» уравнения TdS ≥ dU+pdV получим dF ≤ - SdT - pdV. (6.5) Так как SdT = 0 иpdV= 0 (при Т = const и V= const), тогда для изохорно-изотермических условий (dF)v,T≤ 0. (6.6) В закрытых (замкнутых) системах при изохорно-ихотермических условиях: если dF < 0, то процесс протекает самопроизвольно; если dF > 0, то процесс не протекает; если dF = 0, то система находится в состоянии равновесия. Энергия Гиббса как изобарно-изотермичесий потенциал. Для изобарно-изотермических условий р = const , T = const. Преобразуем объединенное уравнение первого и второго законов термодинамики:  как  (6.7)Проинтегрируем это выражение:  или .Введем обозначение  - это энергия Гиббса. (6.8)Тогда    ,  ,  То есть энергия Гиббса G – это термодинамический потенциал, так как его изменение равно полезной работе при протекании обратимого процесса в системе. Для необратимого процесса  В случае для обратимого и необратимого процесса справедливо выражение  (6.9)Энергия Гиббса равна  , но  Поэтому  отсюда  . (6.10) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, Дж/кмоль
Дж/моль
спарение
лавление