Хомич В.А. - Основы химической термодинамики (2009) (1). Контрольные вопросы для самопроверки знаний по разделу дисциплины физической химии Химическая термодинамика

• Название: Контрольные вопросы для самопроверки знаний по разделу дисциплины физической химии Химическая термодинамика
• Дата: 08.05.2023
• Размер: 0.87 Mb.
• Имя файла: Хомич В.А. - Основы химической термодинамики (2009) (1).doc
• Тип: Контрольные вопросы; #1114115
• страница: 3 из 3

Энергия Гиббса G – эта часть энтальпии, которая может быть превращена в работу; поэтому она называется свободной энергией.

В выражение для энергии Гиббса подставим энергию Гельмгольца, которая определяется как F= U - TS. Тогда получим, что или . (6.11)
Энергия Гиббса, как критерии возможности протекания процесса.

Продифференцируем выражение , получим



Вместо TdS подставим его значение из объединенного уравнения первого и второго законов термодинамики Тогда

или

(6.12)

В изобарно-изотермических условиях и

. (6.13)

То есть dG является критерием возможности протекания процесса в замкнутой (закрытой) системе в изобарно-изотермических условиях. При этом

• 
  если dG < 0, то процесс протекает самопроизвольно;
  
• 
  если dG > 0, то процесс самопроизвольно не протекает;
  
• 
  если dG = 0, то система находится в состоянии равновесия.
  

Характеристической функцией называется такая функция состояния системы, посредством которой или ее производных могут быть выражены в явной форме термодинамические свойства системы. Характеристическими функциями являются:

1. 
   внутренняя энергия U ,
   
2. 
   энтальпия H,
   
3. 
   изохорно-изотермический потенциал F,
   
4. 
   изобарно-изотермический потенциал G,
   
5. 
   энтропия S.
   

Определим значение частных производных основных характеристических функций.

Известно, что для любой функции от переменных её полный дифференциал может быть представлен выражением

,

где - частные производные этой функции по соответствующей переменной при сохранении постоянного значения остальных переменных.

Из объединенного уравнения первого и второго закона термодинамики: выводим выражение для изменения внутренней энергии:

. (6.14)

Дифференцируем выражение

Н = U + pV: .

Вместо подставляем выражение (6.14), получаем

(6.15)

Таким образом, из уравнения (6.14) следует, что а из уравнения (6.15) - .

Запишем выражение полных дифференциалов dU и dH.

(6.16)

. (6.17)

Сопоставляя уравнение (6.16) с уравнением (6.14) и уравнение (6.17) с уравнением (6.15) можно заключить, что

, (6.18, 6.19)

, . (6.20, 6.21)

Эти соотношения показывают физический смысл частных производных внутренней энергии и энтальпии.

Запишем выражения для полных дифференциалов энергии Гельмгольца и энергии Гиббса: , .

Рассмотрим F как функцию от T и V, а Gкак функцию T и р. Их полные дифференциалы равны:


, (6.22)

. (6.23)

Сопоставляя эти выражения с уравнениями (6.5): и (6.12): приходим к выводу, что

, , (6.24, 6.25)

, . (6.26, 6.27)

Изменение изохорного потенциала с изменением температуры при постоянном объеме определяется энтропией. Изменение изохорного потенциала с изменением объема при постоянной температуре определяется давлением.

Изменение изобарного потенциала с температурой при постоянном давлении определяется энтропией. Изменение изобарного потенциала с изменением давления при постоянной температуре определяется объемом.

Уравнения Гиббса-Гельмгольца. Запишем выражения для энергии Гельмгольца и энергии Гиббса: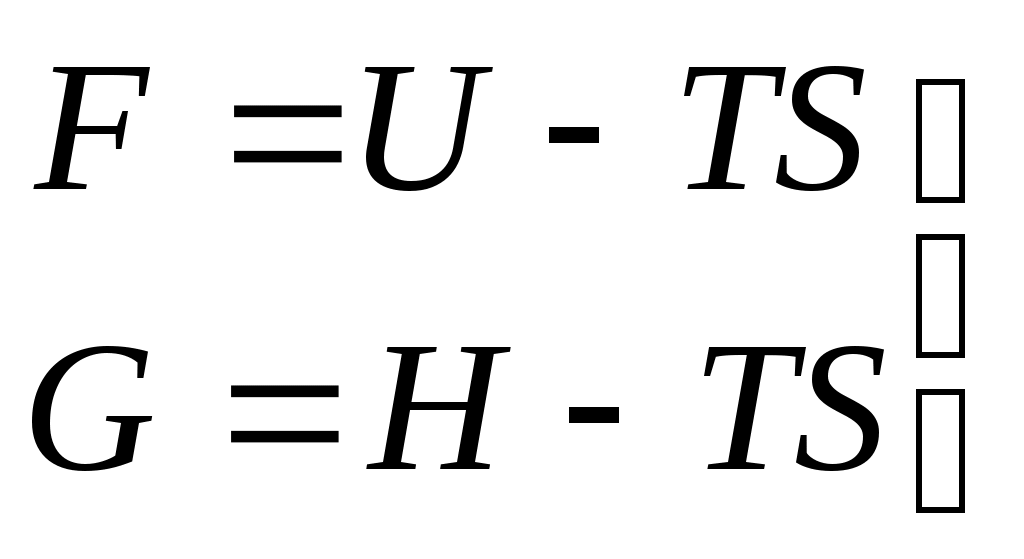

.

Подставим в эти уравнения, вместо энтропии равные ей производные потенциалов, получаем соотношения: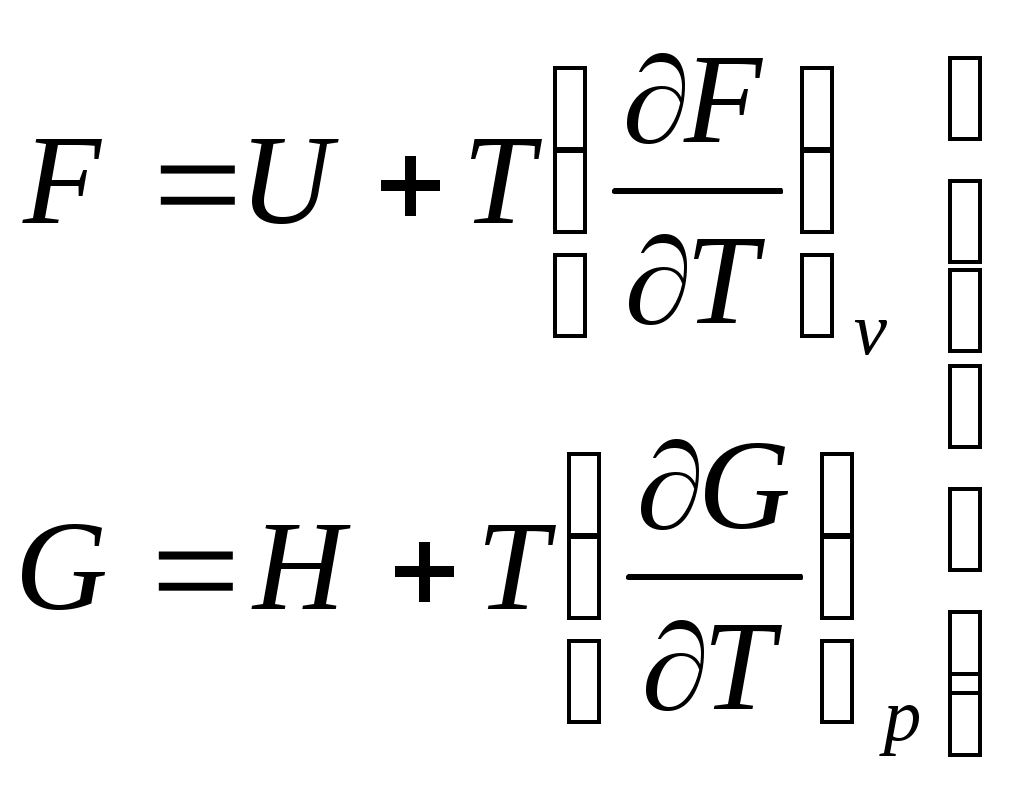

.

Для изменения 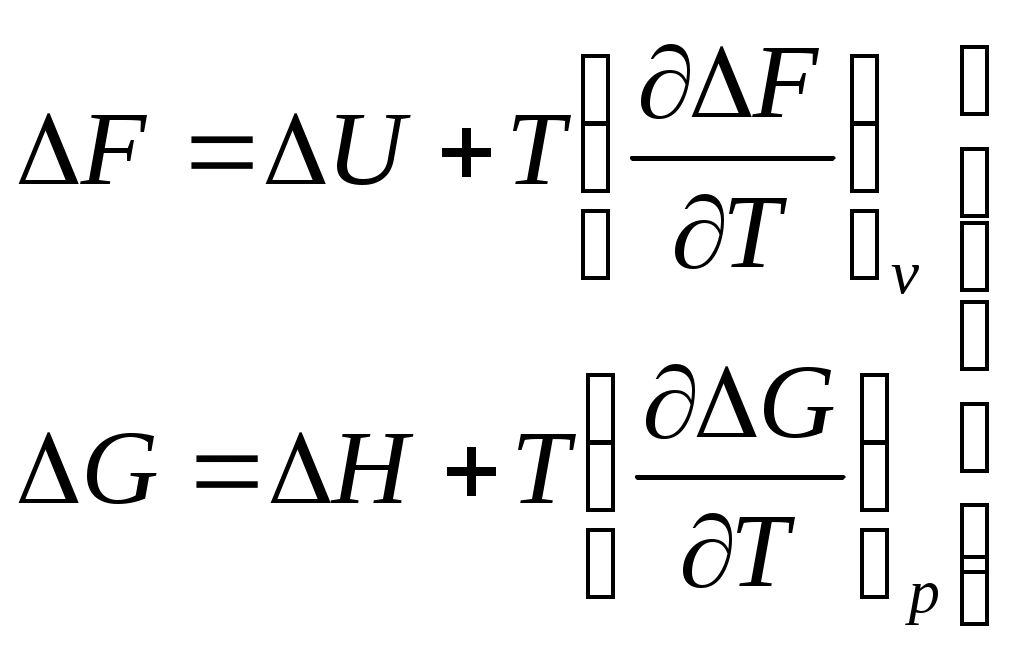этих функций в результате процесса получим:

. (6.28, 6.29)

Уравнения (6.28 и 6.29) - это уравнения Гиббса-Гельмгольца.

Химический потенциал. Для изучения растворов и гетерогенных систем, состоящих из 2-х и более веществ необходимо рассматривать системы, где состав и масса могут быть непостоянными вследствие химической реакции, испарения, кристаллизации и т.д. Изобарный потенциал является функцией не только Т и р, но и количества n₁, n₂, n₃,…, n_j молей компонентов.

,



(6.30)

Химический потенциал вещества в смешанной фазе равен его парциальному изобарному потенциалу. Он численно равен приращению изобарного потенциала раствора, происходящему при добавлении одного моль данного компонента к такому количеству раствора, при котором (при ) его состав не меняется.



или

При : .

Математическое выражение условия равновесия системы с переменным числом молей компонентов: … (6.31)

Представим , что из фазы α в фазу β, переходит dn₁ молей 1-го компонента.

α

β

Условие фазового равновесия для 1-го компонента:

,

,

. (6.32)

При фазовом равновесии химический потенциал каждого компонента во всех фазах одинаков.

Л е к ц и я 7
СТАТИСТИЧЕСКИЙ ХАРАКТЕР

ВТОРОГО ЗАКОНА ТЕРМОДИНАМИКИ
План лекции: Статистический характер второго закона термодинамики. Термодинамическая вероятность состояния системы. Уравнение Больцмана-Планка. Границы применимости второго закона термодинамики.
Второй закон термодинамики можно назвать законом возрастания энтропии при самопроизвольном процессе в изолированной системе. В связи с этим очень важно выяснить физические причины необратимости реальных процессов, сопровождающихся возрастанием энтропии.

Смысл второго закона термодинамики можно понять более глубоко исходя из молекулярно-кинетической теории. Рассмотрим уравнение . В него входят такие параметры, как температура и теплота. Температура является мерой интенсивности теплового движения молекул; теплота – неупорядоченная форма обмена энергии между различными частями системы вследствие хаотического движения частиц. Следовательно, возрастание энтропии в самопроизвольных процессах отражает закономерные изменения в молекулярно-кинетическом состоянии системы.

Характер зависимости энтропии идеального газа от температуры и давления показывает, что энтропия S, может служить мерой беспорядка в расположении и движении молекул. Возрастание энтропии связано с самопроизвольным переходом вещества из состояния со строго упорядоченным расположением частиц в состояние с большим и наибольшим молекулярным беспорядком. Максимальной энтропии отвечало бы состояние газа с совершенно равномерным распределением хаотически движущихся частиц по объему. Однако, в каждый момент времени, в результате беспорядочного движения молекул, имеются местные отклонения от равномерного распределения: временное увеличение концентрации молекул в одних участках объема и уменьшение в других. Поэтому можно говорить о более или менее вероятных состояниях системы. Термин «вероятность состояния» равнозначен по смыслу понятию «беспорядок». Энтропия, является мерой вероятности состояния системы. Это открытие способствовало развитию статистической термодинамики.

Макросостоянием системы называется состояние, заданное термодинамическими параметрами. Это состояние из большого числа частиц. Микросостояние – это непосредственно ненаблюдаемое состояние молекул, атомов, ионов и др. частиц, характеризуемое координатами их положения в пространстве и скоростью их движения. В статистической термодинамике при подсчете вероятности состояния исходят из того, что одно макросостояние системы, например газа, при определенной температуре и давлении, может быть осуществлено большим числом микросостояний с любым распределением частиц по координатам и скоростям. Поскольку частицы газа постоянно и хаотически движутся, микросостояния постоянно чередуются. Однако любое микросостояние равновероятно. Число микросостояний, определяющих данное макросостояние, называется термодинамической вероятностью состояния системы.

Допустим, что имеется всего три молекулы (обозначим цифрами), которые размещаются в двух ячейках фазового пространства (обозначим клетками). Рассмотрим макросостояние, когда в одной ячейке имеется 2 молекулы, а в другой одна. Данное макросостояние реализуется тремя перестановками молекул между ячейками, то есть тремя микросостояниями:
п ервое микросостояние
в торое микросостояние
т ретье микросостояние
Если в системе находится N молекул, то общее число перестановок будет N!. Поделив N! на число перестановок N_i! в каждой ячейке и исключив их тем самым из подсчета, получим термодинамическую вероятность:

, (7.1)

где - число молекул в каждой фазовой ячейке, причем N=N₁+N₂+N₃+…

Процесс выравнивания микросостояний, идущий в естественных условиях самопроизвольно и с возрастанием энтропии, приводит к росту термодинамической вероятности. Термодинамическая вероятность характеризует ту или иную степень беспорядка в сообществе частиц, из которых состоят тела системы. Термодинамическая вероятность, или вероятность состояния системы, оценивается энтропией.

Связь между энтропией и термодинамической вероятностью указывает статистическую природу второго закона термодинамики. Больцман Л. сделал допущение, что энтропия есть некоторая функция вероятности, S = f (W). В классической термодинамике доказывается, что в самопроизвольном процессе энтропии возрастает. С точки зрения статистической термодинамики этот же процесс сопровождается возрастанием вероятности W. При равновесии S и W принимают свои максимальные значения. Вид функции S = f (W) определяется уравнением Больцмана-Планка:

. (7.2)

Константа Больцмана kдолжна иметь размерность энтропии.

, (7.3)

здесь N₀ – число Авогадро, равное 6,02 10²³.
Границы применимости второго закона термодинамики. Статистический характер второго закона термодинамики приводит к заключению, что увеличение энтропии в самопроизвольных процессах указывает на наиболее вероятные пути развития процессов в изолированной системе. Невозможность процесса следует принимать лишь как его малую вероятность по сравнению с обратным. Поэтому второй закон термодинамики нужно рассматривать как закон вероятности. Он тем точнее соблюдается, чем больше размеры системы.

Действие второго закона нельзя распространять на микросистемы. Но также неправомерно распространять второй закон на вселенную. Второй закон термодинамики применим лишь к изолированной системе ограниченных масштабов. Вселенная же существует неограниченно во времени и пространстве.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется системой? В чем заключается отличие изолированной, открытой и закрытой систем?

2. Является ли химическая реакция термодинамическим процессом?

3. Приведите примеры экстенсивных и интенсивных параметров. Может ли экстенсивный параметр стать интенсивным?

4. Соответствует ли первый закон термодинамики принципу эквивалентности работы и энергии? Запишите математическое выражение первого закона.

5. Внутренняя энергия, энтальпия, теплота и работа. Что является функцией состояния, а что функцией процесса?

6. Каким функциям состояния системы равны тепловые эффекты в процессах, протекающих при постоянных давлении, объеме?

7. Чему равна разница между теплоемкостями при постоянном давлении и постоянном объеме?

8. Какими уравнениями выражается температурная зависимость теплоемкости?

9. Какие условия применения закона Гесса? Какие следствия закона Гесса используются для расчета тепловых эффектов физико-химических процессов?

10. Каким уравнением представлена зависимость теплового эффекта от теплоемкости и температуры?

11. Какими характеристиками обладают самопроизвольные (спонтанные) процессы?

12. Запишите аналитическое выражение второго закона термодинамики.

13. Приведите расчетные формулы изменения энтропии в простейших термодинамических процессах: адиабатическом, изотермическом, изохорическом и изобарическом.

14. Какое значение имеет постулат Планка?

15. Приведите расчетные формулы изменения энтропии при фазовых переходах и при нагревании вещества.

16. Для каких систем с использованием энтропии можно определить направление протекания самопроизвольного процесса?

17. Какую зависимость представляет уравнение Клайперона-Клаузиуса? Для определения какой характеристики при агрегатных превращениях оно применяется?

18. Почему энергия Гельмгольца является термодинамическим потенциалом? Почему энергия Гельмгольца является свободной энергией?

19. Почему энергия Гиббса является термодинамическим потенциалом? Почему энергия Гиббса является свободной энергией?

20. Почему внутренняя энергия, энтальпия, свободная энергия Гельмгольца, свободная энергия Гиббса являются характеристическими функциями?

21. На каком основании энергия Гиббса и энергия Гельмгольца используются в качестве критериев направления самопроизвольных процессов и равновесия в неизолированных системах?

22. Какое математическое выражение представляет объединенное уравнение первого и второго законов термодинамики?

23. Какие зависимости термодинамических потенциалов представляют уравнения Гиббса-Гельмгольца?

24. Химический потенциал является функцией состояния системы или функцией процесса? Это экстенсивный или интенсивный параметр?

25. Чем обусловлен статистический характер второго закона термодинамики?

26. Что называется термодинамической вероятностью состояния системы? Запишите уравнение Больцмана-Планка.
Библиографический список
1. Стромберг А.Г. Физическая химия: Учеб. /А.Г. Стромберг, Д.П. Семченко. – М.: Высш. шк., 2006. – 527 с.

2. Физическая химия. В 2-х кн. Кн.1. Строение вещества. Термодинамика: Учеб. / К.С. Краснов, Воробьев, И.Н. Годнев и др.; Под ред. К.С. Краснова. - М.: Высш. шк., 2007. – 512 с.

Содержание
Лекция 1. ВВЕДЕНИЕ………………………………………………………...3

Лекция 2. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ………………………...6

Лекция 3. ТЕРМОХИМИЯ…………………………………………………..13

Лекция 4. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ………………………..20

Лекция 5. ТЕРМОДИНАМИКА АГРЕГАТНЫХ ПРЕВРАЩЕНИЙ……..29

Лекция 6. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ………………….33

Лекция 7. СТАТИСТИЧЕСКИЙ ХАРАКТЕР ВТОРОГО ЗАКОНА

ТЕРМОДИНАМИКИ……………………………………………….40

Контрольные вопросы……………………………………………………….44

Библиографический список…………………………………………………46

Учебное издание


Хомич Вера Алексеевна

Редактор Т.И.Калинина

Подписано к печати

Формат 60x90 1/16. Бумага ксероксная

Оперативный способ печати

Гарнитура Times New Roman

Усл. п.л. 2,5, уч. – изд. л. 2,5

Тираж 50 экз. Заказ

Цена договорная

Издательство СибАДИ

644099, Омск, ул. П.Некрасова, 10

___________________________________
Отпечатано в ПЦ издательства СибАДИ

644099, Омск, ул. П.Некрасова, 10