КОНТРОЛЬНЫЕ ВОПРОСЫ. Контрольные вопросы испытания и события
 Скачать 29.8 Kb. Скачать 29.8 Kb.
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Испытания и события. 2. Случайные, достоверные и невозможные события. 3. Сумма и произведение событий. 4. Противоположные события. 5. Несовместимые и совместимые события. 6. Полная система событий. 7. Классическое определение вероятности. 8. Свойства вероятности. 9. Статистическое определение вероятности. 10. Теоремы сложения вероятностей несовместимых событий. 11. Условная вероятность. 12. Независимые и зависимые события. 13. Теорема умножения вероятностей. 14. Теорема сложения вероятностей совместимых событий. 15. Вероятность появления хотя бы одного из n независимых событий. 16. Формула полной вероятности, формула Байеса. 17. Сочетания. 18. Схема Бернулли, постановка задачи. 19. Формула Бернулли. 20. Наивероятнейшая частота. 21. Локальная формула Лапласа. 22. Свойства и график кривой Гаусса. 23. Интегральная формула Лапласа. 24. Свойства и график интегральной функции Лапласа. 25. Что такое случайная величина? Дискретные и непрерывные случайные величины. 26. Закон распределения дискретной случайной величины. 27. Биноминальный закон распределения. 28. Числовые характеристики случайной величины, их вероятностный смысл. 29. Что такое интегральная функция распределения вероятностей случайной величины? Ее свойства и график. 30. Что такое дифференциальная функция распределения (плотность вероятности)? Каковы ее свойства? 31. Связь между интегральной и дифференциальной функциями распределения непрерывной случайной величины. 32. Числовые характеристики непрерывной случайной величины. 33. Нормальное распределение. График дифференциальной функции. 34. Вероятность попадания непрерывной случайной величины в за- данный интервал. A 35. Закон больших чисел. Неравенства Маркова и Чебышева. Теоремы Чебышева и Бернулли. 1. Испытания и события. Испытание – это изначальное понятие, разъясняется как действие, явление, наблюдение, опыт и проч. Событие – эторезультат (исход) испытания. События обозначаются прописными буквами: А, B, С, D, Е… Примеры: 1) испытание – выстрел по мишени: событие А – попадание в цель, событие В – промах; 2) испытание – бросание монеты: событие Г – выпал орел, событие R – выпала решка; 3) испытание – сдача экзамена: – событие А – экзамен сдан; – событие А1 – получена оценка «отлично»; – событие А2 – получена оценка «хорошо»; – событие А3 – получена оценка «удовлетворительно»; – событие В – экзамен не сдан; 4) испытание – участник турнира завершил шахматную партию: событие А – выигрыш; событие В – проигрыш; событие С – ничья. События называются: – совместными, если в результате испытания наступление одного из событий не исключает появления других (в примере 3 это события А и А1; А и А2; А и А3); – несовместными (несовместимыми), если в одном и том же испытании появление одного из событий исключает появление других (примеры 1, 2 и 4); – единственно возможными, если в результате испытания, хотя бы одно из событий обязательно произойдет (примеры 1,2,3 и 4); – равновозможными, если нет оснований считать появление какого-либо из событий более возможным по отношению к другим, т. е. все события имеют равные шансы (только пример 2). 2. Случайные, достоверные и невозможные события. Так как Р(А) = 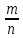 , где количество благоприятных исходов m находится в пределах от 0 доn, то вероятность любого события принимает значения только от нуля до единицы включительно: , где количество благоприятных исходов m находится в пределах от 0 доn, то вероятность любого события принимает значения только от нуля до единицы включительно: 0 ≤ Р(А) ≤ 1. Достоверным называется событие, которое обязательно наступит в результате испытания. Для него все исходы благоприятны, т. е. m = n. Поэтому его вероятность Р(А) = 1. Например, достоверным событием является извлечение из урны красного шара, если все шары в урне красные. Невозможным называется событие, которое в результате испытания заведомо не произойдет. Для него благоприятных исходов нет, т. е.m= 0, поэтому его вероятность Р(А) = 0. Например, невозможным событием является извлечение из урны красного шара, если в урне красных шаров нет. Случайным называется событие, которое в результате испытания может произойти или не произойти. Для него есть как благоприятные, так и неблагоприятные исходы (0< m< n), поэтому его вероятность: 0 < Р(А) < 1. Для задания вероятности часто используют проценты. При этом безразмерное числовое значение вероятности умножают на 100%. Например: Р(А) = 0,8 (80%); Р(В) = 0,052 (5,2%). Если бракованная продукция завода составляет 9%, а событие С – взятое наугад изделие бракованное, то Р(С) = 9% /100% = 0,09. Вероятность служит числовой мерой объективной возможности наступления события. 3. Сумма и произведение событий. Определение 1. Суммой двух событий А и В называется новое событие, состоящее в наступлении хотя бы одного из данных событий, обозначается: А + В. Если А и В – совместные события, то их сумма А + В означает наступление или события А, или события В, или обоих событий. Если А и В – несовместные события, то их сумма означает наступление или события А, или события В: А + В = (А или В). Определение 2. Произведением двух событий А и В называется новое событие, состоящее в совместном наступлении этих событий, обозначается: А·В = (А и В). Если А и В – совместные события, то их произведение А·В означает одновременное наступление и события А, и события В. Если А и В – несовместные события, то их произведение А·В является невозможным событием, поэтому его вероятность Р(А·В) = 0. Совместное появление событий называют их совмещением. Аналогично можно ввести понятия суммы и произведения для любого конечного количества событий. 4. Противоположные события. Если полная группа событий содержит только два события, то такие события называются противоположными. Их обозначают: А и 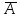 (событие (событие 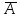 читается не А). читается не А).Из определения полной группы событий вытекает, что противоположные события А и 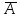 несовместны и единственно возможны, следовательно, сумма их вероятностей равна единице: несовместны и единственно возможны, следовательно, сумма их вероятностей равна единице:Р(А) + Р( 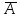 ) = 1. ) = 1.Отсюда находим вероятность противоположного события 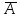 : :Р( 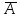 ) = 1– Р(А). ) = 1– Р(А).5. Несовместимые и совместимые события. – совместными, если в результате испытания наступление одного из событий не исключает появления других (в примере 3 это события А и А1; А и А2; А и А3); – несовместными (несовместимыми), если в одном и том же испытании появление одного из событий исключает появление других (примеры 1, 2 и 4); 6. Полная система событий. Единичный, отдельный исход испытания называется элементарным событием. Элементарные исходы образуют полную систему, если они: 1) попарно несовместны; 2) единственно возможны; 3) по каждому из них можно судить о появлении или непоявлении любого другого события, не обязательно элементарного. 7. Классическое определение вероятности. Вероятностью событияAназывается число P(A), равное отношению количества элементарных исходов m, благоприятствующих событию A, к общему количеству n всех равновозможных элементарных (т.е. единственно возможных и попарно несовместных) исходов: Р(А) = 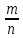 . . 8. Свойства вероятности. Основные свойства вероятности проще всего определить, исходя из аксиоматического определения вероятности. 1) вероятность невозможного события (пустого множества {\displaystyle \varnothing }) равна нулю:{\displaystyle \mathbf {P} \{\varnothing \}=0;} Это следует из того, что каждое событие можно представить как сумму этого события и невозможного события, что в силу аддитивности и конечности вероятностной меры означает, что вероятность невозможного события должна быть равна нулю. 2) если событие A включается («входит») в событие B, то есть {\displaystyle A\subset B}, то есть наступление события A влечёт также наступление события B, то:{\displaystyle \mathbf {P} \{A\}\leqslant \mathbf {P} \{B\};} Это следует из неотрицательности и аддитивности вероятностной меры, так как событие {\displaystyle B}, возможно, «содержит» кроме события {\displaystyle A}ещё какие-то другие события, несовместные с {\displaystyle A}. 3) вероятность каждого события {\displaystyle A} находится от 0 до 1, то есть удовлетворяет неравенствам:{\displaystyle 0\leqslant \mathbf {P} \{A\}\leqslant 1;} Первая часть неравенства (неотрицательность) утверждается аксиоматически, а вторая следует из предыдущего свойства с учётом того, что любое событие «входит» в {\displaystyle X}, а для {\displaystyle X}аксиоматически предполагается {\displaystyle \mathbf {P} \{X\}=1}. 4) вероятность наступления события {\displaystyle B\setminus A}, где {\displaystyle A\subset B}, заключающегося в наступлении события {\displaystyle B} при одновременном ненаступлении события {\displaystyle A}, равна:{\displaystyle \mathbf {P} \{B\setminus A\}=\mathbf {P} \{B\}-\mathbf {P} \{A\};} Это следует из аддитивности вероятности для несовместных событий и из того, что события {\displaystyle A} и {\displaystyle B\setminus A} являются несовместными по условию, а их сумма равна событию {\displaystyle B}. 5) вероятность события {\displaystyle {\bar {A}}}, противоположного событию {\displaystyle A}, равна:{\displaystyle \mathbf {P} \{{\bar {A}}\}=1-\mathbf {P} \{A\};} Это следует из предыдущего свойства, если в качестве множества {\displaystyle B} использовать всё пространство {\displaystyle X} и учесть, что {\displaystyle \mathbf {P} \{X\}=1}. 6) (теорема сложения вероятностей) вероятность наступления хотя бы одного из (то есть суммы) произвольных (не обязательно несовместных) двух событий {\displaystyle A} и {\displaystyle B} равна:{\displaystyle \mathbf {P} \{A+B\}=\mathbf {P} \{A\}+\mathbf {P} \{B\}-\mathbf {P} \{AB\}.} Это свойство можно получить, если представить объединение двух произвольных множеств как объединение двух непересекающихся — первого и разности между вторым и пересечением исходных множеств: {\displaystyle A+B=A+(B\setminus (AB))}. Отсюда учитывая аддитивность вероятности для непересекающихся множеств и формулу для вероятности разности (см. свойство 4) множеств, получаем требуемое свойство. Для трех совместных событий формула сложения вероятностей усложняется Р(А+В+С)=Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС) При увеличении числа слагаемых формула сложения становится всё более и более громоздкой, но принцип её построения остаётся прежним: сначала суммируются вероятности событий взятых по одиночке, затем вычитаются вероятности всех по парных комбинаций событий, прибавляются вероятности событий взятых тройками, вычитаются вероятности комбинаций событий взятых четверками и т.д. Свойства вероятности события: 1. Вероятность достоверного события равна 1. Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т.е. m = n и, следовательно, P(Ω) = m/n = n/n = 1. 2. Вероятность невозможного события равна 0. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е. m = 0, откуда: P(Ø) = m/n = 0/n = 0. 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0 Замечание. Из определения вероятности следует, что элементарные события являются равновероятными, т. е. обладают одной и той же вероятностью. +События, вероятности которых очень малы (близки к нулю) или очень велики (близки к единице), называются соответственно практически невозможными или практически достоверными событиями. 9. Статистическое определение вероятности. Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях. В отличие от «математической» вероятности Р(А), рассматриваемой в классическом определении, статистическая вер-ть является характеристикой опытной, экспериментальной. Если Р(А) есть доля случаев, благоприятствующих событию А, которая определяется непосредственно, без каких-либо испытаний, то есть доля техФактически произведенных испытаний, в которых событие А появилось. Статистическое определение вер-ти, как и понятия и методы теории веро-тей в целом, применимы не к любым событиям с неопределенным исходом, которые в житейской практике считаются случайными, а только к тем из них, которые обладают определенными свойствами. 1) Рассматриваемые события д.б. исходами только тех испытаний, которые м.б. воспроизведены неограниченное число раз при одном и том же комплексе условий. 2) События должны обладать так называемой статистической устойчивостью, или устойчивостью относительных частот. Это означает, что в различных сериях испытаний относительная частота (частость) события изменяется незначительно (тем меньше, чем больше число испытаний), колеблясь около постоянного числа. Оказалось, что этим постоянным числом является вероятность события. Факт приближения относительной частоты, или частости, события к его вер-ти при числа испытаний, сводящихся к схеме случаев, подтверждается многочисленными массовыми экспериментами, проводимыми разными лицами со времен возникновения теории вер-тей. 3) Число испытаний, в результате которых появляется событие А, должно быть достаточно велико, ибо только в этом случае можно считать вер-ть события Р(А) приближенно равной ее относительной частоте. Резюмируя, можно сказать, что теория вер-тей изучает лишь такие события, в отношении которых имеет смысл не только утверждение об их случайности, но и возможна объективная оценка относительной частоты их появления. Так, утверждение, что при выполнении определенного комплекса условий S вероятность события = р, означает не только случайность события А, но и определенную, достаточно близкую к р, долю появлений события А при большом числе испытаний; а значит, выражает определенную объективную (хотя и своеобразную) связь между комплексом условий S и событием А (не зависящую от субъективных суждений о наличии этой связи того или иного лица). И даже просто существование вероятности р (когда само значение р неизвестно) сохраняет качественно суть этого утверждения, выделенную курсивом. Замечание: 1) Статистическая вер-ь может быть найдена только после проведения опытов, а для классической вероятности опыты не нужны. 2) Статистическая вер-ть получается различной для разных серий опытов, однако при достаточно большом количестве опытов практически достоверно, что статистическая вер-ть будет сколь угодно мало отличатся от классической вер-ти (устойчивость статистической вер-ти). Классическое определение вероятности имеет ряд недостатков. Во-первых, должно быть известно общее количество элементарных исходов n и количество благоприятных исходов m. Во-вторых, все элементарные исходы должны быть равновозможными. На практике эти условия, как правило, не выполняются. Поэтому для практических нужд чаще пользуются статистическим понятием вероятности. 10. Теоремы сложения вероятностей несовместимых событий. |
