Задание 1. Контрольные вопросы Кв 1
 Скачать 27.75 Kb. Скачать 27.75 Kb.
|
|
Задание 1 №3 лёд Δ = xизм – xд. Δ = 0.5 – 0 = 0.5 кипящая вода Δ = xизм – xд. Δ = 101 – 100 = 1 =  * 100% * 100% =  * 100% = 0.66 * 100% = 0.66Ответ: 0.66 oC №5 макс = 60+2 = 62 мин = 60-2 = 58 допуст. погрешность = 62-58 = 4 Δ = --- №6 Δ =1.21 - 1.2 = 0.01 δ =  100 % = 0.82% 100 % = 0.82%Ответ: относительная погрешность> относительной погрешности батареи, значит, батарея не годна к эксплуатации №7 δ1 = - 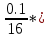 100 % = -0.625 100 % = -0.625δ2 = -  100 % = -0.25 100 % = -0.25Ответ: δ1 = -0.625, δ2 = -0.25 Контрольные вопросы Кв 1 Абсолютная погрешность Δ – это погрешность, выраженная в единицах измеряемой величины и определяемая по формуле (1.1). По формуле (1.1) погрешность рассчитывается в тех случаях, когда действительное значение физической величины известно – это задачи поверки и градуировки средств измерений. В таких задачах на вход средства измерений подают эталонное значение физической величины, которое и принимается за xд. Разность показаний средства измерений и значения эталона и будет представлять собой абсолютную погрешность с соответствующим знаком: Δ = xизм – xд. (1.1) Пример. Необходимо определить погрешность весов. Для этого на платформу весов ставят эталонную гирю 1 кг и снимают показания весов – 1,002 кг. По формуле (1.1) находим, что абсолютная погрешность весов в данной точке шкалы; Δ = 1,002 – 1,000 = 0,002 кг. При этом не принимается во внимание, что масса гири имеет некоторую допустимую погрешность, зависящую от класса точности гири. Если класс точности гири соответствует требованиям к эталону для данных конкретных весов, то считается, что погрешность массы гири равна нулю. Масса гири здесь представляет собой действительное значение массы, относительно которого рассчитывается погрешность. Другой пример. Погрешность рабочего вольтметра определяют методом сличения с эталонным вольтметром. Для этого оба вольтметра подключают к одному и тому же источнику напряжения. Считается, что погрешность эталонного вольтметра равна нулю, то есть его показание представляет собой действительное значение напряжения. Пусть рабочий вольтметр показывает 4,035 В, а эталонный вольтметр – 4,060 В, тогда абсолютная погрешность рабочего вольтметра Δ = 4,035 – 4,060 = – 0,025 В. Во всех задачах подобных, описанным в этих двух примерах, погрешность эталона должна быть в нормированное число раз меньше погрешности рабочего средства измерений. Часто используется отношение погрешностей эталона и рабочего средства измерений 1/3 и менее (1/4; 1/5 и т. д.). При рабочих измерениях эталон не используется, действительное значение величины xд не известно и формула (1.1) неприменима. В таких задачах абсолютную погрешность рассчитывают на основе известной относительной погрешности δ или приведенной погрешности γ средства измерений, которые в свою очередь определяют на основе класса точности данного рабочего средства измерений. При многократном измерении в качестве действительного значения xд принимается среднее арифметическое ряда отдельных измерений, входящих в данный ряд. Относительная погрешность – это погрешность, выраженная отношением абсолютной погрешности Δ к действительному значению величины. Относительную погрешность δ находят из выражения  Относительную погрешность допускается выражать в относительных единицах, в этом случае в формуле (1.2) множитель 100 % отсутствует. Приведенная погрешность – это относительная погрешность, в которой абсолютная погрешность средства измерений отнесена к условно принятому значению XN, постоянному на всем диапазоне измерений или его части, так называемому нормирующему значению; 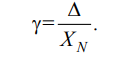 где XN – нормирующее значение. За нормирующее значение чаще всего принимают верхний предел измерений средства измерений. В зависимости от знака Δ, значения δ и γ могут быть как положительными, так и отрицательными. Кв 2 По формуле (1.1) погрешность рассчитывается в тех случаях, когда действительное значение физической величины известно – это задачи поверки и градуировки средств измерений. Кв 3 Истинное значение физической величины xист – это значение физической величины, которое идеальным образом характеризует в количественном и качественном отношении данную физическую величину. Истинное значение физической величины всегда неизвестно, поскольку дать его абсолютно точную количественную оценку невозможно. Кв 4 Погрешность метода измерений (методическая погрешность) – это составляющая погрешности измерения, обусловленная несовершенством принятого метода измерений. Отметим, что в современных нормативных документах [1], вместо термина «методическая погрешность» используется термин «погрешность метода измерений». Вместе с тем, в многочисленной литературе и некоторых государ- 8 ственных стандартах по-прежнему употребляется термин «методическая погрешность». Погрешность метода измерений в основном проявляется как систематическая погрешность, но иногда может проявляться и как случайная погрешность. Особенностью погрешностей метода измерений является их индивидуальность, связанная не только с применением данного метода или физического принципа, но и с его конкретным воплощением. Из многих возможных причин погрешности метода измерений укажем две характерные причины: - неточность модели физического процесса, на котором базируется средство измерений; - неверное применение средства измерений. В нормативной документации на СИ погрешность метода измерений обычно не указывается, однако могут быть приведены методические рекомендации по правильному применению данного СИ. Пример. При взвешивании тела на аналитических рычажных весах будет допущена систематическая методическая погрешность, если не будет вноситься поправка на различие выталкивающих сил, действующих со стороны воздуха на взвешиваемое тело и гири. Действительно, на взвешиваемое тело и гири действуют направленные вверх силы Архимеда. Объемы взвешиваемого тела и гирь в общем случае различны, соответственно будут отличаться и действующие на них выталкивающие силы. Пример. У термометра, размещенного на солнце, показания будут завышенными из-за дополнительного нагрева солнечным излучением. Термометр будет нагрет сильнее, чем окружающий воздух, методическая погрешность имеет знак «плюс». Пример. При измерении напряжения вольтметром по его входной цепи протекает ток, зависящий от входного сопротивления вольтметра. Поэтому измеренное напряжение будет меньше действительного значения. Методическая погрешность в этом случае имеет знак «минус» и может быть достаточно точно рассчитана по входному сопротивлению вольтметра и выходному сопротивлению контролируемой цепи. Для снижения методической погрешности входное сопротивления прибора должно быть как можно больше, по сравнению с выходным сопротивлением контролируемой цепи (в идеале сопротивление вольтметра должно быть бесконечно большим). Кв 5 Инструментальная погрешность – это составляющая погрешности измерения, обусловленная погрешностью применяемого СИ. Например, инструментальная погрешность может быть обусловлена нелинейностью преобразования сигнала, инерционностью СИ, его нестабильностью, изменением условий эксплуатации (температуры окружающей среды и других внешних воздействующих факторов). Инструментальная погрешность складывается из основной и дополнительных погрешностей, рассмотренных ниже. Суммарная инструментальная погрешность в реальных условиях применения средства измерений может рассчитываться на основе двух моделей погрешности [2]. Модель I является наиболее полной и учитывает пять составляющих погрешности средства измерений: систематическую составляющую основной погрешности; случайную составляющую основной погрешности; случайную составляющую основной погрешности, обусловленную гистерезисом; дополнительные погрешности, обусловленные действием влияющих величин и неинформативных параметров входного сигнала; динамическую погрешность. Δи – инструментальная погрешность. Кв 6 Субъективная погрешность – это составляющая систематической погрешности измерения, обусловленная индивидуальными особенностями конкретного оператора. Например, при снятии показаний по стрелочному отсчетному устройству большое значение имеет правильное направление взгляда оператора. Другой пример. При постоянном измеряемом напряжении показания цифрового вольтметра хаотически изменяются на 2-3 последних цифры. Один оператор будет брать средние значения, другой – минимальные (максимальные) значения. Кв 7 Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности могут быть предсказаны, обнаружены и существенно уменьшены путем введения поправок при определении результата измерений. Поправки определяются и вычисляются с некоторой погрешностью, часть систематических погрешностей оказывается необнаруженной, поэтому существует понятие неисключенной систематической погрешности. Кв 8 Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений физической величины постоянного размера, проведенных с одинаковой тщательностью в одинаковых условиях. Случайная погрешность неустранима и проявляются в виде разброса результатов многократных измерений. Предельные значения случайной погрешности могут быть оценены на основе теории случайных процессов и математической статистики. Уменьшение слу- 10 чайной погрешности возможно путем проведения многократных измерений и усреднения их результатов. Кв 9 Грубая погрешность (промах) – это погрешность, которая при исправных средствах измерений и корректных действиях оператора не должна появляться. Причины промахов – неправильная запись показаний и иные ошибки оператора, сбои в работе аппаратуры, скачки напряжения в сети, сотрясения пола и другие. При однократном измерении промах может быть обнаружен только путем логического анализа или сопоставления результата с априорным представлением о нем. В сомнительных случаях проводят дополнительные измерения, при необходимости скорректировав методику их выполнения. При многократном измерении одной и той же величины постоянного размера промахи проявляются в том, что результаты отдельных измерений, входящих в один ряд, резко отличаются от остальных результатов этого ряда. Такие промахи выявляют с помощью специальных критериев при обработке результатов измерений. При последующей статистической обработке результат, признанный промахом, не учитывают. Кв 10 Дополнительная погрешность СИ – составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений. Примеры: дополнительные погрешности, вызванные изменением температуры окружающей среды, напряжения питания и других влияющих факторов. Кв 11 Статическая погрешность СИ – погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную. Иными словами, статическая погрешность – это погрешность статического измерения. Статическое измерение имеет место, если измеряемая величина постоянна или изменяется настолько медленно, что этим изменением в процессе измерения можно пренебречь. 11 Пример. Масса человека не является постоянной величиной. Однако в процессе взвешивания масса человека не успевает заметно измениться, поэтому мы считаем, что это статическое измерение. Динамическая погрешность СИ – погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерения) физической величины. Эта дополнительная динамическая составляющая погрешности обусловлена инерционными свойствами СИ, не способного отслеживать быстрое изменение измеряемой величины. Отметим, что лишь немногие виды СИ пригодны для проведения динамических измерений. Пример. Мы хотим зарегистрировать изменение температуры газов, образующихся при быстром горении. Однако датчик температуры не может моментально прогреться до измеряемой температуры, поэтому мгновенные измеренные температуры будут ниже действительных значений (динамическая погрешность в данном случае отрицательна). Кв 12 Основная погрешность СИ – это погрешность СИ, применяемого в нормальных условиях. Δо – основная погрешность средства измерений. Кв 13 Суммарная погрешность результата измерений в общем случае определяется путем геометрического суммирования отдельных составляющих. Например, если помимо инструментальной погрешности имеется неисключенная погрешность метода измерений, то суммарную погрешность находим по формуле: 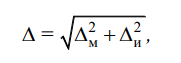 |
