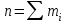Главная страница
Навигация по странице:

  • РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ Задание

  • Определение степени согласованности мнений экспертов Задание

    		•

    метрология 5 вариант 2 и 3 задание. Результатов измерений


    Скачать 46.18 Kb.
    НазваниеРезультатов измерений
    Дата13.01.2023
    Размер46.18 Kb.
    Формат файлаdocx
    Имя файламетрология 5 вариант 2 и 3 задание.docx
    ТипЗакон
    #885434

    Задание 2. Вариант 5


    ПОСТРОЕНИЕ МОДЕЛЕЙ ЗАКОНА РАСПРЕДЕЛЕНИЯ

    РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

    Задание:

    При n - кратном независимом измерении одной и той же физической величины постоянного размера на табло прибора в случайном порядке появились значения (табл.1).

    Таблица 1 – Исходные данные

    хi
    90,1
    90,11
    90,12
    90,13
    90,14
    90,15
    90,16
    90,17
    90,18
    90,19
    90,2

    mi
    1+К
    2 + К
    5 + К
    10 +К
    20+К
    24+К
    19+К
    11+К
    5 + К

    2 + К
    1 + К

    mi
    6
    7
    10
    15
    25
    29
    24
    16
    10
    7
    6

    Примечание: К – шифр студента.

    Каждое хi значение появилось mi раз. Построить по этим данным графики плотности распределения вероятности и функции распределения вероятности.

    Решение:

    Решение задачи производится в следующей последовательности. Определяется вероятность появления на табло прибора результата хi по формуле:


    (2.2)

    где n –общее число измерений или объем выборки.

    Q - измеряемая величина;

    [Q] - известный размер в единицах СИ.


    Общее число измерений или объем выборки определяется по формуле:

    (2.3)


    В данном случае n= 155.

    Вероятность появления на табло прибора результата 90,1 равно:


    Следующим этапом определяются значения функции распределения вероятности F(xi):

    (2.4)


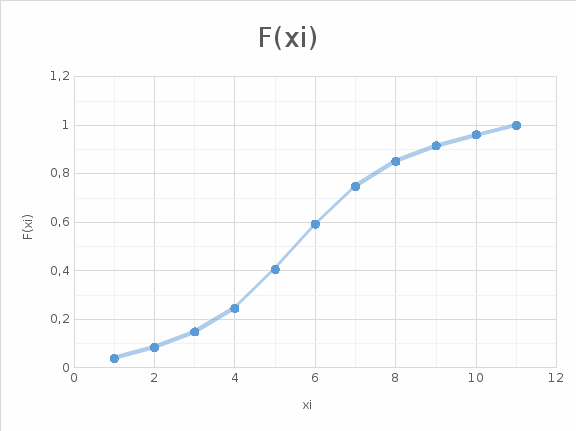
    Для результата измерения 90,1 значение F(xi-1) принимается равным 0. В этом случае значение F(x1) приравнивается к значению P(x1) и будет равным 0,0387. Значение функции распределения вероятности для результата измерения 90,11 определяется следующим образом:


    Необходимо отметить, что значение F(xi) для последнего значения должно получиться близким к 1. Аналогично производятся расчеты для остальных значений. Результаты расчетов оформляются в виде таблицы (табл. 2).
    Таблица 2 - Результаты расчетов

    № п/п
    хi
    mi
    P(xi)
    F(xi)

    1
    90,10
    6
    0,0387
    0,0387

    2
    90, 11
    7
    0,0452
    0,0839

    3
    90,12
    10
    0,0645
    0,1484

    4
    90,13
    15
    0,0967
    0,2451

    5
    90,14
    25
    0,161
    0,4061

    6
    90,15
    29
    0,187
    0,5931

    7
    90,16
    24
    0,155
    0,7481

    8
    90,17
    16
    0,103
    0,8511

    9
    90,18
    10
    0,0645
    0,9156

    10
    90,19
    7
    0,0452
    0,9608

    11
    90,20
    6
    0,0387
    0,9995


    По данным табл. 2 строятся графики соответствующих функций (рис. 2.2).


    а) график P(xi)




    б) график F(xi)



    Рисунок 1 – Графики плотности распределения вероятности и функции распределения вероятности



    Задание 3. Вариант 5


    Определение степени согласованности мнений экспертов

    Задание:

    Определить степень согласованности мнений экспертов по данным, приведенным в табл. 3.

    Таблица 3

    Номер объекта экспертизы
    Оценка эксперта

    1-го
    2-го
    3-го
    4-го
    5-го

    1
    9
    11
    8
    6
    11

    2
    11
    10
    10
    6
    9

    3
    9
    6
    11
    7
    10

    4
    6
    7
    7
    9
    6

    5
    10
    11
    8
    10
    9

    6
    10
    7
    11
    9
    7

    7
    6
    8
    9
    7
    8


    Решение

    а) Определение среднего значения суммы рангов (сумма оценок каждого эксперта по каждому виду продукции. Например, для первого объекта экспертизы сумма рангов равна: Тогда среднее значение суммы рангов определяется из отношения суммы сумм рангов к общему числу объектов экспертизы:

    б) Определение отклонений суммы рангов каждого объекта экспертизы от среднего арифметического рангов. Для примера берется первый объект экспертизы:



    в) Определение суммы квадратов отклонений суммы рангов каждого объекта экспертизы от среднего арифметического рангов и их суммы. В данном примере эта величина принимает значение: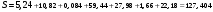



    г) Определение коэффициента конкордации:



    Результаты расчетов сводятся в табл. 4.

    Таблица 4

    Результаты расчетов

    № объекта
    Оценка эксперта
    Сумма рангов
    Откл-е от среднего
    Квадрат откл-й

    1го
    2го
    3го
    4го
    5го

    1
    9
    11
    8
    6
    11
    45
    2,29
    5,24

    2
    11
    10
    10
    6
    9
    46
    3,29
    10,82

    3
    9
    6
    11
    7
    10
    43
    0,29
    0,084

    4
    6
    7
    7
    9
    6
    35
    -7,71
    59,44

    5
    10
    11
    8
    10
    9
    48
    5,29
    27,98

    6
    10
    7
    11
    9
    7
    44
    1,29
    1,66

    7
    6
    8
    9
    7
    8
    38
    -4,71
    22,18



    написать администратору сайта