Методы количественного анализа. Контрольнокурсовое задание Методы количественного анализа
 Скачать 115.89 Kb. Скачать 115.89 Kb.
|
|
«Синергия» Контрольно-курсовое задание Методы количественного анализа Задание 1 Файл Облигации.XLS содержит значения следующих переменных: Дата – текущая дата. 10 - летние облигации – значения учетной ставки 10-летних облигаций Министерства финансов США (процентное изменение по отношению к величине учетной ставки на момент закрытия предыдущих торгов). DJIA - значения индекса Доу Джонса на момент закрытия предыдущих торгов. Постройте график (один) временных рядов для ежедневных значений индекса, его ежедневных процентных изменений. Вычислите основные статистические характеристики переменных. Определите ежедневные изменения индекса DJIA, выраженные в процентах. Насколько соответствуют этим данным правила областей (правило трёх сигм (3σ))? Ответ Динамика индекса Доу-Джонса представлена на рис. 1. 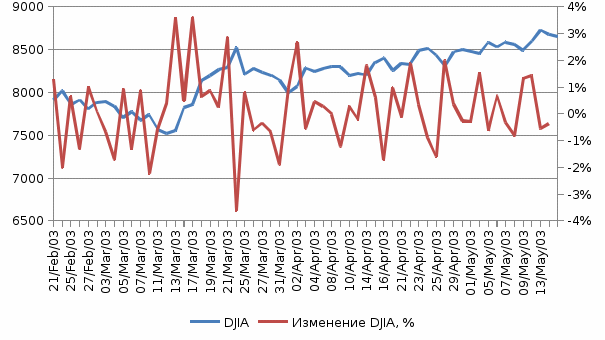 Рисунок 1 - Индекс Доу-Джонса и его ежедневные процентные изменения Статистические характеристики переменных рассчитаны с помощью модуля Анализ данных Описательная статистика. Результат приведен в табл. 1. Таблица 1 - Статистические характеристики переменных
Среднее значение по 10-летним облигациям за период составило3,837. Медиана – 3,89. Это означает, что в половине случаев значение учетной ставки было ниже этого уровня, а в половине – выше. Поскольку среднее значение и медиана близки по значению, это говорит об однородности совокупности. Разница между минимальным и максимальным значением учетной ставки за период составила 0,55. Стандартное отклонение равно 0,1387, т.е. величина учетной ставки отклоняется от среднего значения на 0,1387. Коэффициент вариации (отношение стандартного отклонения к среднему значению) равно 3,6%, т.е. совокупность данных является однородной. Среднее значение индекса Доу-Джонса за период равно 8197,58, медиана – 8257,61. Близость этих показателей говорит о том, что совокупность однородна. Стандартное отклонение равно 311,36, т.е. отдельные значения индекса отклоняются от средней величины в среднем на 311,36. Разница между наибольшим и наименьшим значением за период составила 1202,67. Коэффициент вариации равен 3,8% (311,36/8197,58*100%). Это говорит о количественной однородности совокупности. Ежедневные изменения индекса Доу-Джонса рассчитаны в столбце D на листе «Облигации». Среднее значение изменений равно 0,16%, стандартное отклонение – 1,38%. Проверим правило трех сигм: Ни одно значение не выходит за пределы интервала -3,96%–4,29%, т.е. данные соответствуют правилу «трех сигм». Задание 2 Для анализа финансовых расчетов с филиалами торговой компании за последние 4 месяца (файл Торговая компания.XLS) собрана информация об операциях поставки товаров, а именно, Филиал№, месяц, категория товара, сумма поставки, сумма поступившей оплаты. Необходимо исследовать данные с помощью инструментария Excel, а также: А) создайте сводную таблицу для вычисления количества операций по каждому филиалу и по каждому месяцу (по всем категориям) Б) создайте сводную таблицу для вычисления общих сумм поставок по каждому филиалу за каждый месяц. Используя полученные данные, постройте соответствующие временные ряды для каждого филиала. В) постройте гистограмму для поступивших оплат для трех категорий поставки. Ответ Рассчитаем, какой удельный вес имеет каждый филиал в общем доходе компании (табл. 2). Таблица 2 - Структура доходов компании по филиалам
Из таблицы видно, что наибольшую долю в оплате имеет филиал №2 (23,1%), а наименьшую – филиал №6 (7,0%). Средний размер оплаты по филиалу равен 50202,29 тыс. руб. Среднемесячное значение оплаты за период равно 87854,5 тыс. руб. (табл. 3). Таблица 3 - Сумма оплаты по месяцам
Самый высокий уровень оплаты наблюдается в июне (137,3% от среднего уровня), а самый низкий – в мае (59,6%). В целом таблица показывает неравномерность объемов продаж по месяцам. Таблица 4 - Структура денежных поступлений по категориям товара
Из таблицы 4 видно, что наибольший удельный вес в доходах компании имеют поступления от продаж и текстиля (74,2%). Второе по значимости место занимает парфюмерия (17,3%). Сводная таблица по количеству операций представлена на рис. 2. 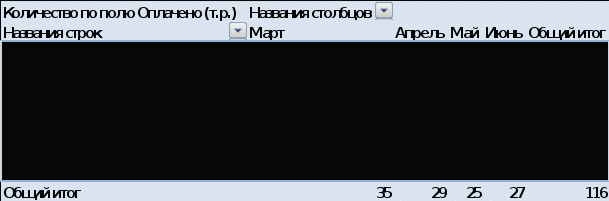 Рисунок 2 - Сводная таблица по количеству операций Из сводной таблицы видно, что за анализируемый период было проведено 116 операций. Больше операций было совершено в марте (35), меньше всего – в мае (25). Наибольшее количество операций пришлось на второй филиал (28), наименьшее – на филиал №7 (11). 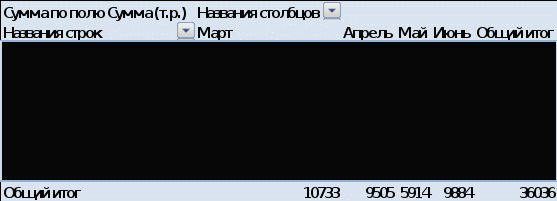 Рисунок 3 - Сводная таблица по сумме поставок Из таблицы видно, что общая величина поставок по всей компании за период составила 36036 тыс. руб. Наибольший объем поставок наблюдается по второму филиалу (7877 тыс. руб.), наименьший – по филиалу №7 (2752 тыс. руб.) 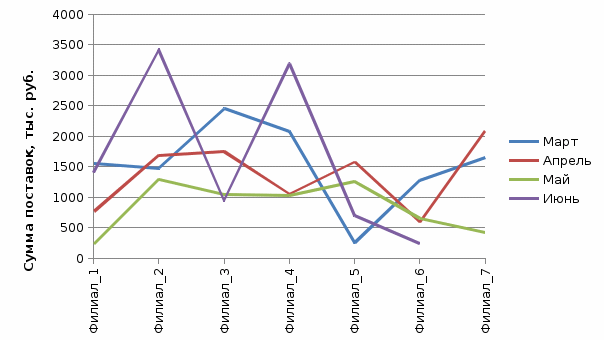 Рисунок 4 - Динамика величины поставок по филиалам 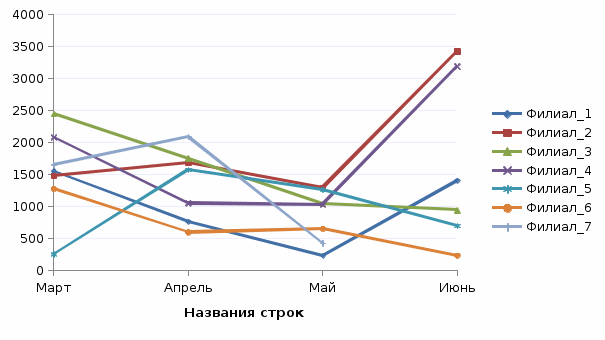 Рисунок 4.1 - Динамика величины поставок по филиалам 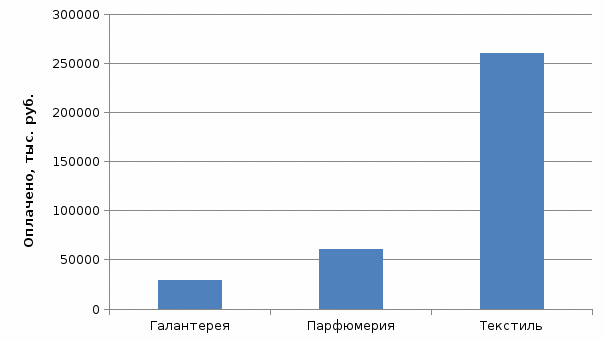 Рисунок 5 - Величина оплаты по категориям товаров Из рис. 5 видно, что наибольшая величина денежных поступлений приходится на текстиль, вторая по значимости категория – парфюмерия. Наименьшая величина оплаты наблюдается по галантерее. Задание 3 Владелец ресторана европейской кухни заинтересовался особенностями заказов, принимаемых на выходные. Он стал записывать количество заказов на различные виды блюд. Предположим, что владельца ресторана интересует также, заказывают ли посетители десерт. Он решил записывать значения еще двух переменных: пол посетителя и заказывал ли он говядину. Результаты этих исследований приведены ниже.
Подготовьте модель (Excel: относительные, абсолютные ссылки) и вычислите: Какова вероятность того, что первый же клиент закажет десерт? Какова вероятность того, что первый клиент не закажет говядину? Какова вероятность того, что первый клиент закажет десерт или говядину? Какова вероятность того, что первый клиент окажется женщиной и не закажет десерт? Какова вероятность того, что первый клиент закажет десерт и говядину? Какова вероятность того, что первый клиент окажется женщиной или не закажет десерт? Предположим, что первый клиент, у которого официант принял заказ, оказался женщиной. Какова вероятность того, что она не закажет десерт? Предположим, первый же клиент заказал говядину. Какова вероятность, что он закажет и десерт? Являются ли пол клиента и заказ десерта статистически независимыми? Являются ли заказ десерта и заказ говядины статистически независимыми? Ответ 1) Вероятность того, что первый же клиент закажет десерт, равна отношению числа ответов «Да» по десерту к общему числу заказов: P = 320 / 600 = 0.533 (53.3%) 2) Вероятность того, что первый клиент не закажет говядину: P = 413 / 600 = 0.688 (68.8%) 3) Вероятность того, что первый клиент закажет десерт или говядину равна сумме вероятностей этих заказов без вероятности их совместного появления: P(A+B) = P(A) + P(B) – P(AB) P(A) = 320 / 600 = 0.533; P(B) = 187 / 600 = 0.312; 0.53 + 0.312 – 0.533 * 0.312 = 0.679 (67.9%) 4) Вероятность того, что первый клиент окажется женщиной и не закажет десерт, рассчитывается по формуле умножения вероятностей: P(AB) = P(A) * P(B) Вероятность того, что клиент окажется женщиной: 464 / 600 = 0,773 (77.3%) Вероятность того, что женщина не закажет десерт: 240 / 464 = 0,517 (51.7%). P = 0.773 * 0.517 = 0.4 (40%) 5) Вероятность того, что первый клиент закажет десерт и говядину, также вычисляется как произведение вероятностей: P = 320 / 600 * 187 / 600 = 0.166 (16.6%) 6) Вероятность того, что первый клиент окажется женщиной или не закажет десерт, можно рассчитать, как разницу между 1 и вероятностью того, что клиент будет мужчиной и закажет десерт: P = 1 - 136 / 600 * 96 / 136 = 0.840 (84%) 7) Вероятность того, что женщина не закажет десерт, равна: P = 240 / 464 = 0.517 (51.7%) 8) Вероятность того, что клиент, заказавший говядину, закажет и десерт: P = 320 / 600 = 0.533 (53.3%) 9) Являются ли пол клиента и заказ десерта статистически независимыми? Статистическая независимость признаков проверяется с помощью критерия χ2 Пирсона: 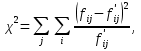 где: Критерий χ2 равен: Табличное значение χ2 для уровня значимости 0,05 и числа степеней свободы k=2-1=1 равно 3,841. Поскольку фактическое значение критерия превышает табличное, это означает, что между признаками существует стохастическая связь. Вывод: пол клиента и заказ десерта не являются статистически независимыми. 10) Являются ли заказ десерта и заказ говядины статистически независимыми По аналогичным вычислениям критерий χ2 равен: Табличное значение χ2 для уровня значимости 0,05 и числа степеней свободы k=2-1=1 равно 3,841. Поскольку фактическое значение критерия превышает табличное, это означает, что между признаками существует стохастическая связь. Вывод: заказ десерта и заказ говядины не являются статистически независимыми. Задание 4 В рабочей книге PIZZA.XLS содержатся данные о 36 порциях пиццы: стоимость в долларах, количество калорий и количество жира в граммах для трех категорий продуктов: сырной пиццы из пиццерии (тип 1), сырной пиццы из супермаркета (тип 2) и острой пиццы из супермаркета (тип 3). Используйте инструмент Сводные таблицы и функции вычисления статистических характеристик. Вычислите распределение частот и процентное распределение для стоимости, калорий и жирности. Постройте кривую распределения (полигон накопленных процентов) для стоимости, калорий и жирности. Изучите аналитически и графически взаимосвязь переменных. Какие выводы можно сделать о стоимости, количестве калорий и жирности каждой из разновидностей пиццы? Ответ Распределение частот для стоимости, калорий и жирности можно построить с помощью инструмента «Гистограмма» из пакета «Анализ данных». Таблица 6 - Распределение пиццы по стоимости
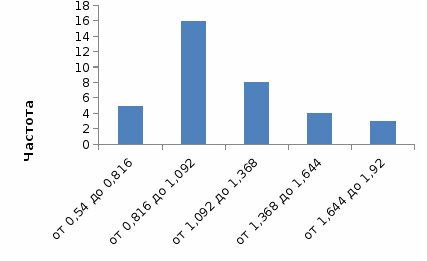 Рисунок 6 - Гистограмма распределения пиццы по стоимости Наибольшую частоту имеет интервал «816-1,092 долл.», т.е. это наиболее распространенная цена на пиццу. Вторым по частоте интервалом (22,2%) является интервал «1,092-1,368 долл.». Цену свыше 1,644 долл. имеют всего 8,3% пицц. Статистические характеристики ряда распределения рассчитаем с помощью инструмента «Описательная статистика» из пакета «Анализ данных» (табл. 7). Таблица 7 - Описательные статистики для стоимости, калорий и жира
Из таблицы видно, что средней ценой на пиццу является 1,099. Медиана несколько ниже – 0,960. Это означает, что в половине случаев пицца дешевле 0,96 долл., а в половине – дороже. Мода с помощью этого инструмента рассчитывается как наиболее часто повторяющееся значение в выборке. Поэтому более информативно будет рассчитать моду по интервальному распределению по формуле: где: Модальным является интервал «0,816-1,092». Мода равна: Таким образом, наиболее распространенная цена на пиццу – 0,976 долл. Самая низкая цена равна 0,54 долл., самая высокая – 1,92. Стандартное отклонение равно 0,329, т.е. цена на пиццу отклоняется от средней величины в среднем на 0,329 долл. Коэффициент вариации равен 29,9%, т.е. совокупность является количественно однородной. 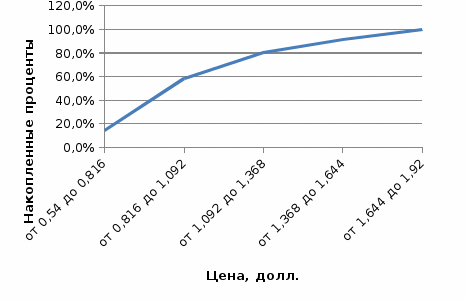 Рисунок 7 - Полигон накопленных процентов для распределения пиццы по стоимости Таблица 8 - Распределение пиццы по калориям
Из таблицы видно, что наиболее распространенной является пицца с калориями 359,2-385,6 (30,6% от совокупности). Второе место по распространенности занимает пицца с числом калорий 332,8-359,2 (22,2%). 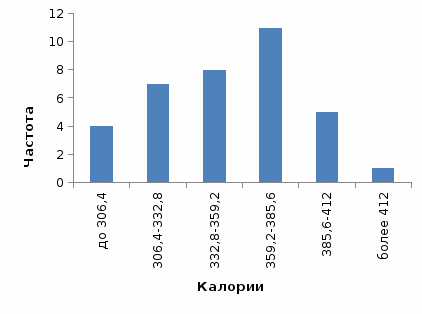 Рисунок 8 - Гистограмма распределения пиццы по калорийности Высококалорийная пицца (с числом калорий более 412) занимает всего 2,8% совокупности. Низкокалорийная пицца (до 306,4 кал.) более распространена – ее удельный вес в совокупности 11,1%. Средняя калорийность пиццы – 351,8 кал., медиана распределения – 354, т.е. в половине случаев в пицце менее 354 кал., а в половине – больше 354 кал. Мода распределения равна: Таким образом, наиболее распространенная калорийность пиццы – 368 кал. Коэффициент вариации равен 10,2%, т.е. совокупность является количественно однородной. Разброс в значениях составляет 132 кал. (разница между максимальной и минимальной калорийностью). 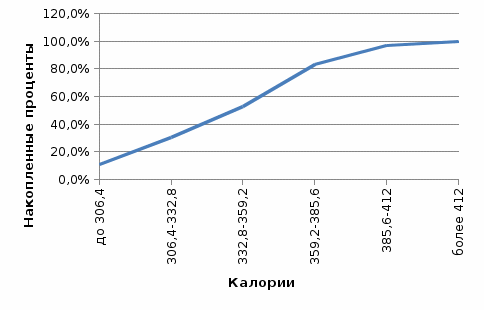 Рисунок 9 - Полигон накопленных процентов для распределения пиццы по калориям Таблица 9 - Распределение пиццы по жиру
Из таблицы видно, что наиболее распространенным значением жирности является 12,8-17,2 (36,1% совокупности). Также очень распространена пицца жирностью 17,2-21,6 (25% совокупности). Пицца с жирностью менее 8,4 встречается редко (доля в совокупности всего 5,6%). Средняя жирность по совокупности равна 15,6, медианная – 14,5. Мода распределения равна: 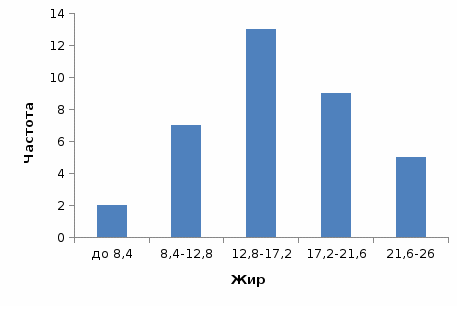 Рисунок 10 - Гистограмма распределения пиццы по жиру Стандартное отклонение равно 5,16, т.е. жирность конкретной пиццы отклоняется от средней величины в среднем на 5,16. Коэффициент вариации равен 33%, т.е. совокупность количественно неоднородна. Из всех рассмотренных показателей (цена, калории, жирность) это самый высокий коэффициент вариации, т.е. именно по жирности пиццы различаются между собой сильнее всего. 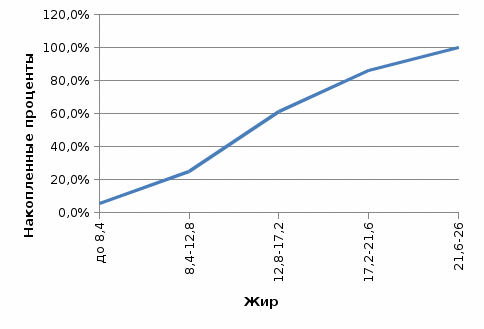 Рисунок 11 - Полигон накопленных процентов для распределения пиццы по жиру Сводная таблица по видам пиццы показывает, что самой дорогой является пицца Chain (средняя цена – 1,451), а самой дешевой – сырная пицца Cheese (средняя цена – 0,998).  Рисунок 12 - Сводная таблица по пицце Самой калорийной и жирной является пицца Пепперони, а наименее калорийной и жирной – сырная пицца. Для оценки взаимосвязи между переменными можно построить диаграммы рассеяния и рассчитать коэффициенты парной корреляции с помощью функции КОРРЕЛ или построить корреляционную матрицу с помощью инструмента «Корреляция» (Анализ данных). 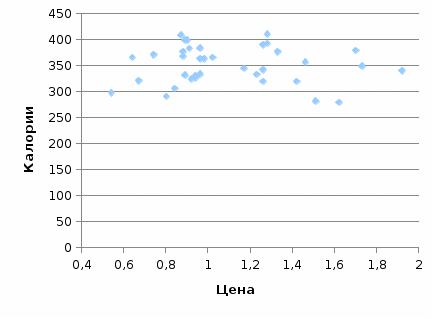 Рисунок 13 - Диаграмма рассеяния между ценой и калорийностью пиццы Из рисунка 13 видно, что между калорийностью и ценой пиццы нет корреляционной связи. 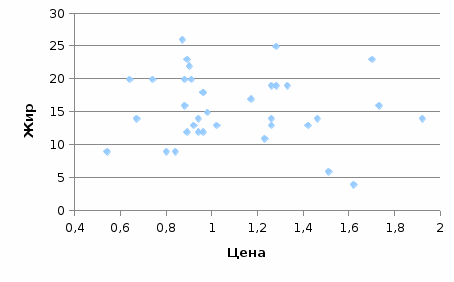 Рисунок 14 - Диаграмма рассеяния между ценой и жирностью пиццы Из рисунка 14 видно, что между жирностью и ценой пиццы нет корреляционной связи. 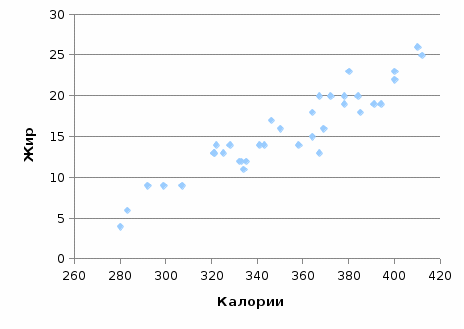 Рисунок 15 - Диаграмма рассеяния между калорийностью и жирностью пиццы Из рис. 15 видно, что между жирностью и калорийностью пиццы есть прямая связь – чем жирнее пицца, тем выше ее калорийность. Проверим сделанные выводы, построив корреляционную матрицу (табл. 10). Таблица 10 - Корреляционная матрица
Из таблицы видно, что единственный значимый коэффициент корреляции (0,9357) наблюдается между жиром и калорийностью, т.е. между этими переменными есть сильная корреляционная связь. Между остальными признаками связи нет. Литература 1. Бизнес-анализ информации. Статистические методы Автор: В. Л. Аббакумов, Т. А. Лезина Издательство: Экономика Достоинствами данной книги являются подробный разбор примеров анализа данных и изложение приемов интерпретации результатов работы статистических процедур. 2. Количественные методы анализа хозяйственной деятельности Автор: Ричард Томас Издательство: Дело и Сервис В книге изложены важнейшие методы количественного анализа деятельности различных предприятий: методы сбора и анализа данных, корреляционно - регрессионный метод, методы прогнозирования, моделирования, управления запасами др. 3. Количественные методы анализа в маркетинге Автор: Под редакцией Т. П. Данько, И. И. Скоробогатых Издательство: Питер В книге описываются количественные методы маркетингового анализа, позволяющие специалисту-маркетологу принимать обоснованные решения, руководствуясь результатами статистической обработки данных и математического моделирования. 4. Рынок ценных бумаг. Количественные методы анализа Автор: В. И. Малюгин Издательство: Дело В учебном пособии последовательно и математически строго излагаются количественные методы анализа рынка ценных бумаг в условиях неопределенности. Описываются вероятностные модели курсов и доходностей ценных бумаг, методы оптимизации структуры портфелей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
