1 вар записка. Корреляционный и регрессионный анализ экспериментальных данных
 Скачать 136.69 Kb. Скачать 136.69 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ВолгГТУ) Кафедра «Технология машиностроения» Семестровая работа по дисциплине «Математическое моделирование технологических процессов тема: «Корреляционный и регрессионный анализ экспериментальных данных» Вариант № 1 Выполнил: студент гр. КТО-325 Василенко Д.И. Проверил: Фролов Е. М. Волгоград 2018 г. Цель работы: провести корреляционный и регрессионный анализ результатов эксперимента. Задачи: Оценить степень тесноты взаимосвязи значений функции отклика со значениями независимой переменной. Определить достоверность данной оценки. Проанализировать условия применимости статистического анализа. Получить линейную регрессионную модель зависимость функции отклика от независимой переменной. Оценить значимость коэффициентов регрессии и адекватность уравнения регрессии. Задание: Таблица 1
Продолжение таблицы 1
1. Для оценки степени тесноты взаимосвязи значений функции отклика со значениями независимой переменной используется коэффициент парной корреляции, рассчитываемый по формуле 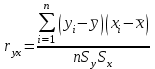 ( (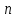 – объем выборки; – объем выборки; 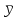 и и 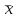 – средние арифметические значения – средние арифметические значения 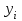 и и 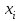 в рассматриваемой выборке; в рассматриваемой выборке; 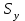 , , 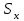 – стандартные отклонения – стандартные отклонения 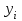 и и 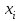 в рассматриваемой выборке). в рассматриваемой выборке).По результатам расчета коэффициент парной корреляции 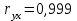 , что больше 0,5. Соответственно можно сделать вывод о наличии тесной взаимосвязи значений функции отклика со значениями независимой переменной. , что больше 0,5. Соответственно можно сделать вывод о наличии тесной взаимосвязи значений функции отклика со значениями независимой переменной.Так как объем рассматриваемой выборки N=69, то для оценки достоверности рассчитанного коэффициента корреляции проверяется нулевая гипотеза 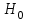 , согласно которой коэффициент корреляции генеральной совокупности равен нулю, посредством критерия Стьюдента. Результаты расчета приведен в таблице 2. , согласно которой коэффициент корреляции генеральной совокупности равен нулю, посредством критерия Стьюдента. Результаты расчета приведен в таблице 2.Таблица 2
Поскольку критическое значение критерия Стьюдента при уровне значимости 0,05 и числе степеней свободы 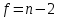 =69–2=67 меньше расчетного, то нулевую гипотезу об отсутствии линейной зависимости между значениями функции отклика и значениями независимой переменной следует отвергнуть и признать коэффициент парной корреляции достоверным. =69–2=67 меньше расчетного, то нулевую гипотезу об отсутствии линейной зависимости между значениями функции отклика и значениями независимой переменной следует отвергнуть и признать коэффициент парной корреляции достоверным.2. Применение корреляционного и регрессионного анализа правомерно и эффективно при соблюдении следующих условий: 2.1. Параметр оптимизации – случайная величина с нормальным законом распределения. Для проверки используется критерий Пирсона 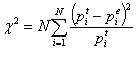 (N – число интервалов, по которому строится эмпирический закон распределения; (N – число интервалов, по которому строится эмпирический закон распределения; 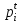 – вероятность попадания значения случайной величины в i-й интервал для теоретического закона распределения; – вероятность попадания значения случайной величины в i-й интервал для теоретического закона распределения; 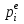 – вероятность попадания значения случайной величины в i-й интервал для эмпирического закона распределения). Результаты расчетов приведены в таблице 3. – вероятность попадания значения случайной величины в i-й интервал для эмпирического закона распределения). Результаты расчетов приведены в таблице 3.Таблица 3
Для ответа на вопрос о принятии нулевой гипотезы о том, что данная случайная величина подчиняется нормальному закону распределения, находится критическое значение критерия Пирсона в зависимости от уровня значимости 0,05 и числа степеней свободы k=s-1-r=9-1-2=6 (s – число интервалов, r – количество параметров предполагаемого распределения. В ходе сравнения наблюдаемого значения критерия Пирсона с теоретическим установили, что наблюдаемое значение критерия меньше теоретического, а соответственно рассматриваемая случайная величина распределена по нормальному закону. 2.2. Дисперсии результатов параллельных опытов должны быть однородны. Так как число опытов при определении каждого значения функции отклика одинаково, то однородность ряда дисперсий оценивается с помощью критерия Кохрена 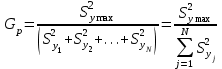 . Результаты расчета приведены в таблице 4. . Результаты расчета приведены в таблице 4.Таблица 4
Табличное значение критерия Кохрена определяется в зависимости от уровня значимости 0,05 и количества степеней свободы f=k-1=3-1=2 (где k количество параллельных опытов). Поскольку расчетное значение критерия Кохрена меньше теоретического, дисперсии считаются однородными. 2.3. Значения независимых переменных должны изменяться с пренебрежимо малыми ошибками по сравнению с ошибкой в определении функции отклика. Считаем, что эксперимент проводится на исправном оборудовании в соответствующих условиях и поэтому ошибки в задании независимых переменных пренебрежимо малы по сравнению с ошибками в определении функции отклика. 2.4. Независимые переменные не должны коррелировать друг с другом. Данное условие не требует проверки, так как в эксперименте участвует только одна независимая переменная. 2.5. Процесс изменения зависимой переменной должен быть стационарным и случайным. Для проверки стационарности процесса строится случайная последовательность значений функции отклика, соответствующая порядку проведения измерений и разбивается на 7 равных отрезков. Для каждого из них рассчитывается дисперсию и с помощью критерия Кохрена устанавливается, являются ли значения дисперсий на каждом из отрезков оценками одной и той же генеральной дисперсии. Результат расчета приведен в таблице 5. Поскольку расчетное значение критерия Кохрена меньше теоретического для уровня значимости 0,05 и количества степеней свободы в знаменателе f=k-1=7-1=6 (где k количество опытов в отрезке), дисперсии на каждом из отрезков являются оценками одной и той же генеральной дисперсии. Таблица 5
Затем проверяется гипотеза о равенстве всех генеральных средних. Чтобы она была справедлива, должно соблюдаться условие  ( 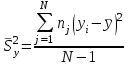 ; ; 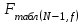 – табличное значение критерия Фишера; – табличное значение критерия Фишера; 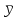 – общее среднее всех элементов отрезков при объединении их в одну выборку). Результаты расчета приведены в таблице 6. – общее среднее всех элементов отрезков при объединении их в одну выборку). Результаты расчета приведены в таблице 6.Таблица 6
Поскольку табличное значение критерия Фишера меньше расчетного, гипотеза о равенстве всех генеральных средних отвергается. Данный результат вызван тем, что при анализе результатов эксперимента не было выполнено требование о расположении значений функции отклика в последовательности, соответствующей порядку проведения измерений. 2.6. Экспериментальные данные должны быть получены из ряда независимых испытаний и образовывать случайную выборку из генеральной совокупности. Данная гипотеза проверяется методом последовательных разностей (Критерий Аббе-Линника). Для чего по значениям выборки, расположенным в последовательности их наблюдения, образуется 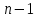 разностей между соседними членами: разностей между соседними членами: 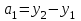 , , 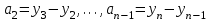 . Затем рассчитывается критерий . Затем рассчитывается критерий 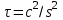 , в котором: , в котором: 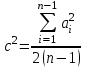 , , 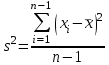 . .Если 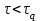 ( (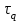 – критическое значение при уровне значимости 0,95), то гипотеза о случайности выборки верна. Результаты расчета представим в таблице 7. – критическое значение при уровне значимости 0,95), то гипотеза о случайности выборки верна. Результаты расчета представим в таблице 7.Таблица 7
На основе результатов расчета делаем вывод, что результаты опытов образовывают случайную выборку из генеральной совокупности. 3. Коэффициенты линейной регрессии рассчитываются по формулам 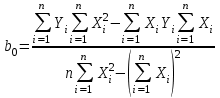 , , 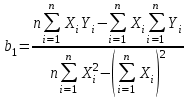 . В рассматриваемом случае . В рассматриваемом случае 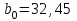 , , 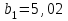 и уравнение линейной регрессии выглядит следующим образом: и уравнение линейной регрессии выглядит следующим образом: 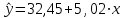 . Построим график для сравнения измеренных значений функции отклика со значениями, полученными по уравнению регрессии (рис. 1). . Построим график для сравнения измеренных значений функции отклика со значениями, полученными по уравнению регрессии (рис. 1).Значимость коэффициентов регрессии проверяется по критерию Стьюдента. Для этого рассчитывается 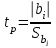 ( (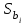 – стандартное отклонение – стандартное отклонение 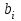 коэффициента регрессии) для каждого коэффициента и сравнивается с критическим значением критерия Стьюдента для уровня значимости 0,05 и числа степеней свободы коэффициента регрессии) для каждого коэффициента и сравнивается с критическим значением критерия Стьюдента для уровня значимости 0,05 и числа степеней свободы 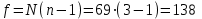 . Коэффициент считается значимым, если . Коэффициент считается значимым, если 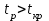 . Так как во всех строках матрицы плана число параллельных опытов одинаково, то . Так как во всех строках матрицы плана число параллельных опытов одинаково, то 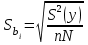 ( (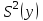 –дисперсия воспроизводимости). Поскольку дисперсии параллельных опытов однородны (установлено в пункте 2.2), то дисперсия воспроизводимости эксперимента равна –дисперсия воспроизводимости). Поскольку дисперсии параллельных опытов однородны (установлено в пункте 2.2), то дисперсия воспроизводимости эксперимента равна  ( ( – дисперсии результатов – дисперсии результатов 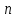 параллельных опытов). параллельных опытов).Результаты расчета представлены в таблице 8. Таблица 8
На основе расчета можно сделать вывод, что оба коэффициента линейной регрессии значимы. Адекватность уравнения регрессии проверяется сравнением дисперсии выборки с дисперсией адекватности. Если дисперсия адекватности существенно отличается от дисперсии выборки, значит уравнение регрессии адекватно. Для оценки адекватности модели вычисляется опытное значение критерия Фишера: 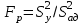 . Дисперсия выборки рассчитывается по формуле . Дисперсия выборки рассчитывается по формуле 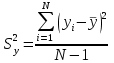 , а дисперсия адекватности – , а дисперсия адекватности – 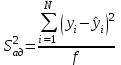 ( 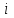 -го опыта; -го опыта; 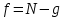 – число степеней свободы; – число степеней свободы; 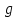 – число коэффициентов регрессии). Если – число коэффициентов регрессии). Если 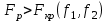 , модель считают адекватной ( , модель считают адекватной (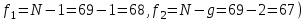 . .Результаты расчета представлены в таблице 9. Таблица 9
На основе расчета можно сделать вывод, что уравнение регрессии дает адекватные результаты. 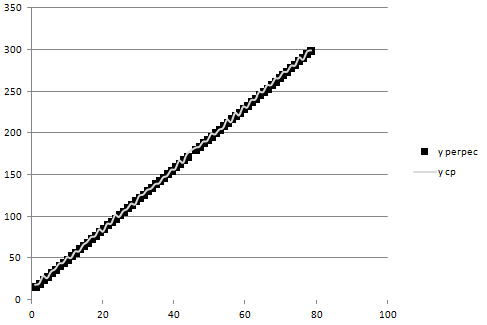 Рисунок 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
