Задачи.Микроэкономика+_1_+для+студентов+задание+_2_+_1_. Кривая производственных возможностей и альтернативные издержки. Задача 1
 Скачать 4.75 Mb. Скачать 4.75 Mb.
|
|
Микроэкономика Кривая производственных возможностей и альтернативные издержки. Задача 1. В стране Z производятся только 2 товара - велосипеды и стиральные машины, причем все имеющиеся ресурсы используются полностью. Варианты производственных комбинаций приведены в таблице. Начертите кривую производственных возможностей. Найдите альтернативные издержки. Отыщите на графике точки M (80 велосипедов и 30 стиральных машин) и N (30 велосипедов и 20 стиральных машин). О чем свидетельствуют эти точки?
Решение: B = 100-90/10-0=1 C = 90-75/20-10= 1,5 D =75-55/30-20=2 E = 55-0/40-30=5,5 Для построения КПВ по горизонтали отложим количество стиральных машин, по вертикали – количество велосипедов.  Точка М – лежит за границей КПВ и свидетельствует о невозможности такого производства при имеющихся ресурсах. Точка N- лежит внутри области КПВ и свидетельствует о неэффективном использовании имеющих ресурсов. Альтернативные издержки по мере продвижения по кривой производственных возможностей возрастают, о чем свидетельствует и форма кривой (выпуклая). Это означает, что производство каждой дополнительной единицы стиральных машин требует отказа от все большего количества велосипедов. Значит, ресурсы, используемые для производства дополнительных стиральных машин, становятся все менее эффективными. Их требуется все большее количество, то есть действует закон возрастания альтернативных затрат. Задача 2. Путешествие из Санкт-Петербурга в Москву занимает 8 часов поездом и 3 часа самолетом (с учетом времени поездки в аэропорт). Стоимость проезда поездом 100 рублей, самолетом — 250 рублей. В путешествие отправляются трое: Андреев, Борисов и Васильев. Часовая ставка оплаты труда Андреева — 20 рублей в час, у Борисова — 30, у Васильева — 50. Каким видом транспорта поедут эти люди? Решение: В данном случае 100 рублей – неизбежные затраты, т. е. при выборе любого вида транспорта меньше затратить невозможно. Поэтому, дополнительными (предельными) затратами являются 250 – 100 = 150 рублей. Неизбежные потери времени составляют 3 часа, дополнительные (предельные) потери равны 8 – 3 = 5 часам. Далее следует сопоставить дополнительные затраты и возможные заработки за дополнительное время. Для Андреева: 150 руб. >20 руб./ч · 5час. Для Борисова: 150 руб. = 30 руб./ч · 5час. Для Васильева: 150 руб. < 50 руб./ч · 5 час. Таким образом, с точки зрения рационального поведения, Андреев поедет поездом, для Борисова безразлично, какой вид транспорта выбрать, а Васильева полетит самолетом. Задача 3. На острове живут 6 человек. Они собирают кокосы и черепаховые яйца. Один человек может собрать либо 20 кокосов, либо 15 яиц. Начертите кривую производственных возможностей экономики острова. Как изменится КПВ. если на остров привезут технику, которая позволит собирать 25 кокосов в день. Решение: Построим кривую производственных возможностей: Если все 6 человек будут собирать только кокосы, то в день у них получиться собрать: 6*20=120 кокосов, если же все жители будут собирать только яйца, то 6*15=90 черепаховых яиц, следовательно, если два человека мы отправим на сбор яиц: 2*15=30 яиц будет собрано, то в тот же день остальные соберут 4*20=80 кокосов и т.д. 
Полезность, предельная норма замещения, бюджетная линия и кривая безразличия Задача 4. Некто потребляет 5 шт. товара А, приносящего ему 8 ед. полезности и 12 шт. товара Б, дающего 18 ед. полезности. Он решил, что ничего не произойдёт, если он будет потреблять 7 шт. товара А и 10 шт. товара Б, которые принесут ему, соответственно 10 и 16 ед. полезности. Определить величину предельной полезности для каждого товара и предельную норму замещения товаров. Решение: Для решения данной задачи используем формулы: а) предельной полезности (MU = ∆TU/∆Q); б) предельной нормы замещения (MRSА/Б = MUА/MUБ). Подставляем данные из условия задачи в формулу предельной полезности и получаем: MUА = (10 – 8) / (7 – 5) = 1 MUБ= (18 – 16) / (12 – 10) = 1 После того, как найдены предельные полезности блага А и блага Б, определяем предельную норму их замещения. MRSА/Б = 1 / 1 Ответ: а) MUА = 1, MUБ = 1; б) MRSА/Б = 1 Задача 5. Заполнить таблицу:
Решение: MU=(TUi-TUi-1)/(Qi-Qi-1); AU=TU/Q Задача 6. На дискотеке Вы можете купить «Пепси» и «Фанту», при этом больше 5 бутылок Вам не выпить. Вы оцениваете для себя полезность напитков так, как представлено в таблице. Что Вы будете пить и в каком количестве, максимизируя полезность?
Решение: Общая полезности напитков = 28-15=13 4 «Пепси» и 1 «Фанта»: TU= 15+13+10+8+10=46+10=56; 3 «Пепси» и 2 «Фанта»: TU= 15+13+10+10+9=38+19=57; 2 «Пепси» и 3 «Фанта»: TU= 15+13+10+9+6=28+25=53; 1 «Пепси» и 4 «Фанта»: TU= 15+10+9+6+3=15+28=43. Сравнивая полученные результаты, делаем вывод: комбинация напитков, состоящая из 3 бутылок «Пепси» и 2 бутылок «Фанты», принесёт наибольшую полезность. Задача 7. Как лучше всего потратить 70р. на завтрак в буфете, если булочка - 20р., стакан сока - 10 р., а их предельная полезность для владельца такова:
Решение: MU – предельная полезность 1,2,3 P – цена благ 1,2,3 (MU1/P1)=( MU2/P2)= (MU3/P3) Ответ: 1 булочку и 2 стакана сока. Спрос, предложение, эластичность спроса, эластичность предложения, рыночное равновесие Задача 8. Как повлияет каждое из следующих событий при всех других равных условиях на спрос жителей конкретной страны на натуральный сок местного производства? 1. выросли цены на газовые напитки; 2. упали цены на импортные консервированные соки; 3. появление на местном рынке новой марки водки; Решение: 1. спрос увеличится т.к это взаимозаменяемые товары; 2. спрос снизится, т.к это взаимозаменяемые товары; 3. не изменится, т.к товары не связанные. Задача 9. Как повлияет при других равных условиях увеличение в 1,5 раза доходов населения на спрос следующих товаров? перловая крупа; красная икра; компьютеры; соль. Решение: 1. Перловая крупа – достаточно дешевая, но не слишком вкусная. Её в основном едят только малоимущие слои населения, более богатые её почти не употребляют, поэтому при увеличении доходов спрос перловой крупы уменьшится. 2. Красная икра – достаточно дорогая, а значит бедные люди и даже средний класс не могут её позволить, но если зарплата увеличится, то уже больше людей смогут её себе позволить, следовательно спрос на неё вырастет. 3. Компьютеры – не являются предметами первой необходимости и люди покупают компьютеры только при наличии более менее адекватных основных потребностей (кров, еда, безопасность), следовательно если зарплаты вырастут, то больше людей смогут себе позволить основные потребности и будут заглядываться на дополнительные, к которым относится компьютер, а значит спрос на него вырастет 4. Соль – бедные и богатые люди примерно одинаковое количество съедают соли, потому что слишком много все равно её не съешь, будь ты хоть миллионером, поэтому спрос останется неизменным. Задача 10. Функция спроса задана таблично. Найти эластичность в каждой точке и на отрезке между ними.
Решение: Для нахождения эластичности в точке используется формула точечной эластичности: 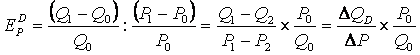 Для нахождения эластичности на отрезке используется формула дуговой эластичности: Для нахождения эластичности на отрезке используется формула дуговой эластичности:  Левая точка Левый отрезок Средняя точка Правый отрезок Задача 11. Спрос задан функцией Qd=20-3Р, Р1=3, Р2=5. Постройте график, как изменится величина спроса? Решение: При цене 3 руб. величина спроса превысит величину предложения: Qd=20-3*3 = 11 Qs=2*3+2 = 8 Qd-Qs= 11-8 = 3 - избыточный спрос. При цене 5 руб. величина предложения превысит величину спроса: Qd=20-3*5 = 5 Qs=2*5+2 = 12 Qs- Qd = 12-5 = 7 – избыточное предложение. 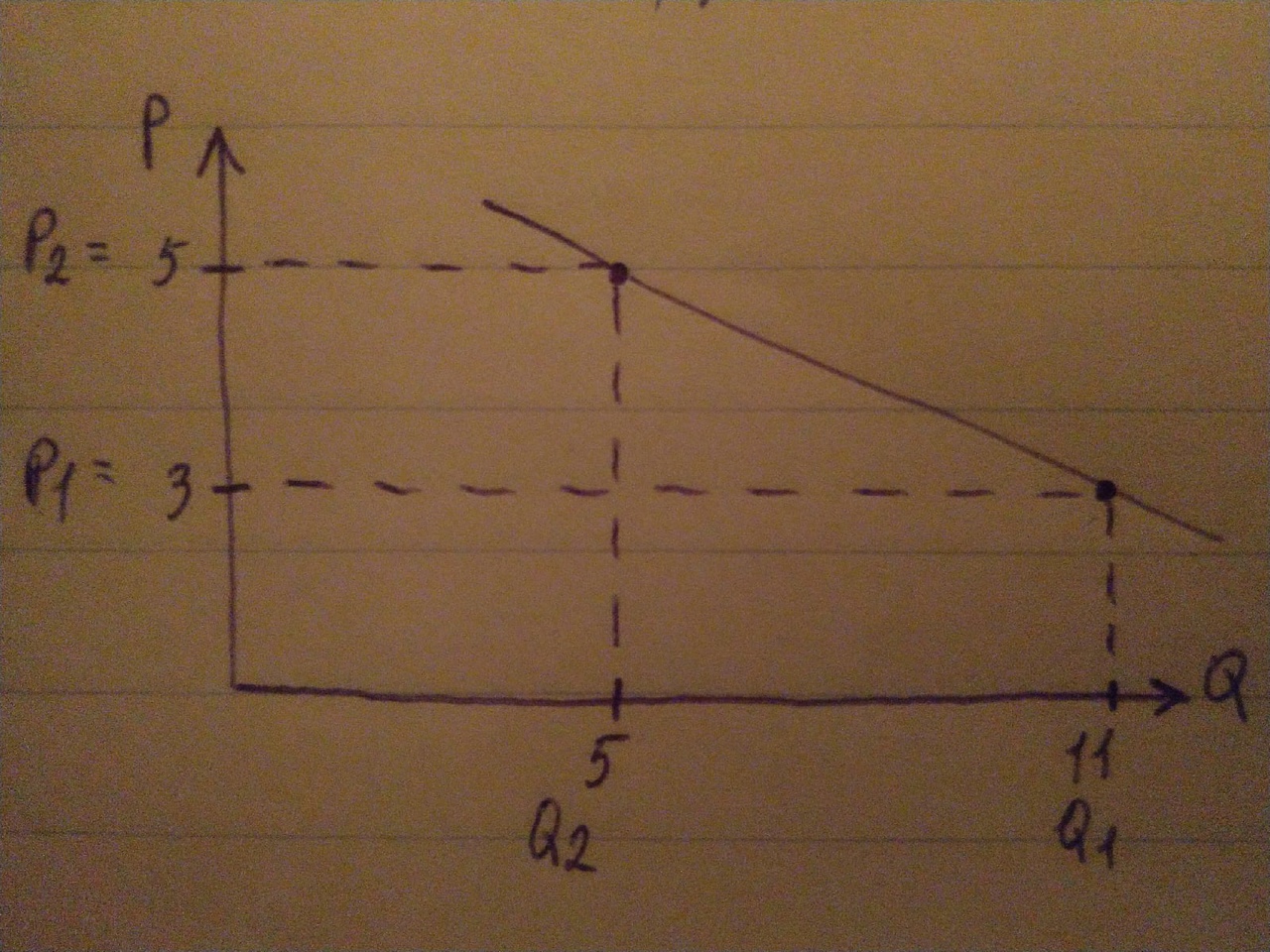 Задача 12. Доход равен 12 д.е. Сколько ед. товара будет куплено, учитывая уровень цен, приведенный в таблице. Постройте кривую спроса.
Решение: 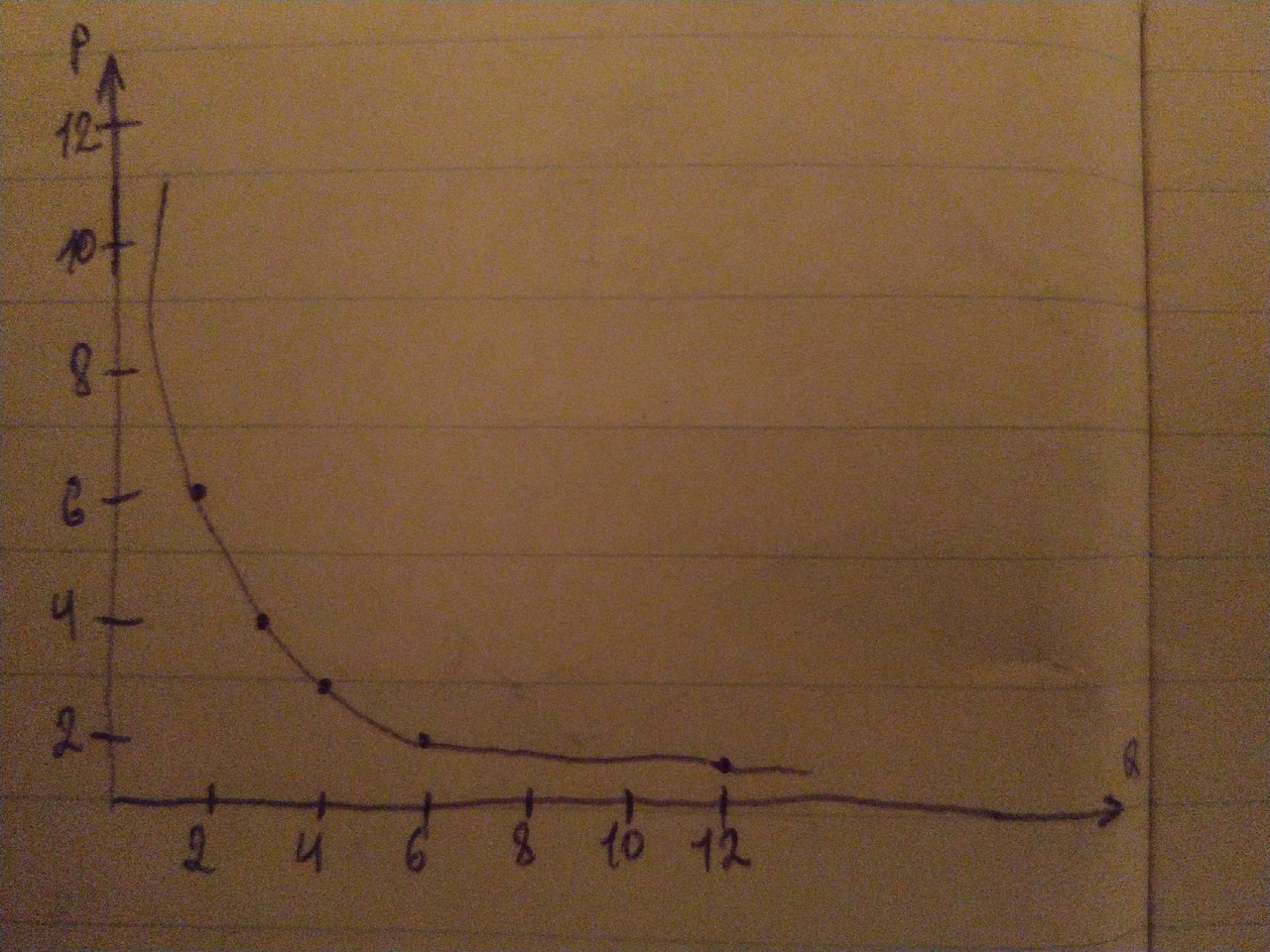 Задача 13. Зависимость объема предложения товара А от его цены представлена в таблице:
Нарисуйте кривую предложения данного товара. Решение: 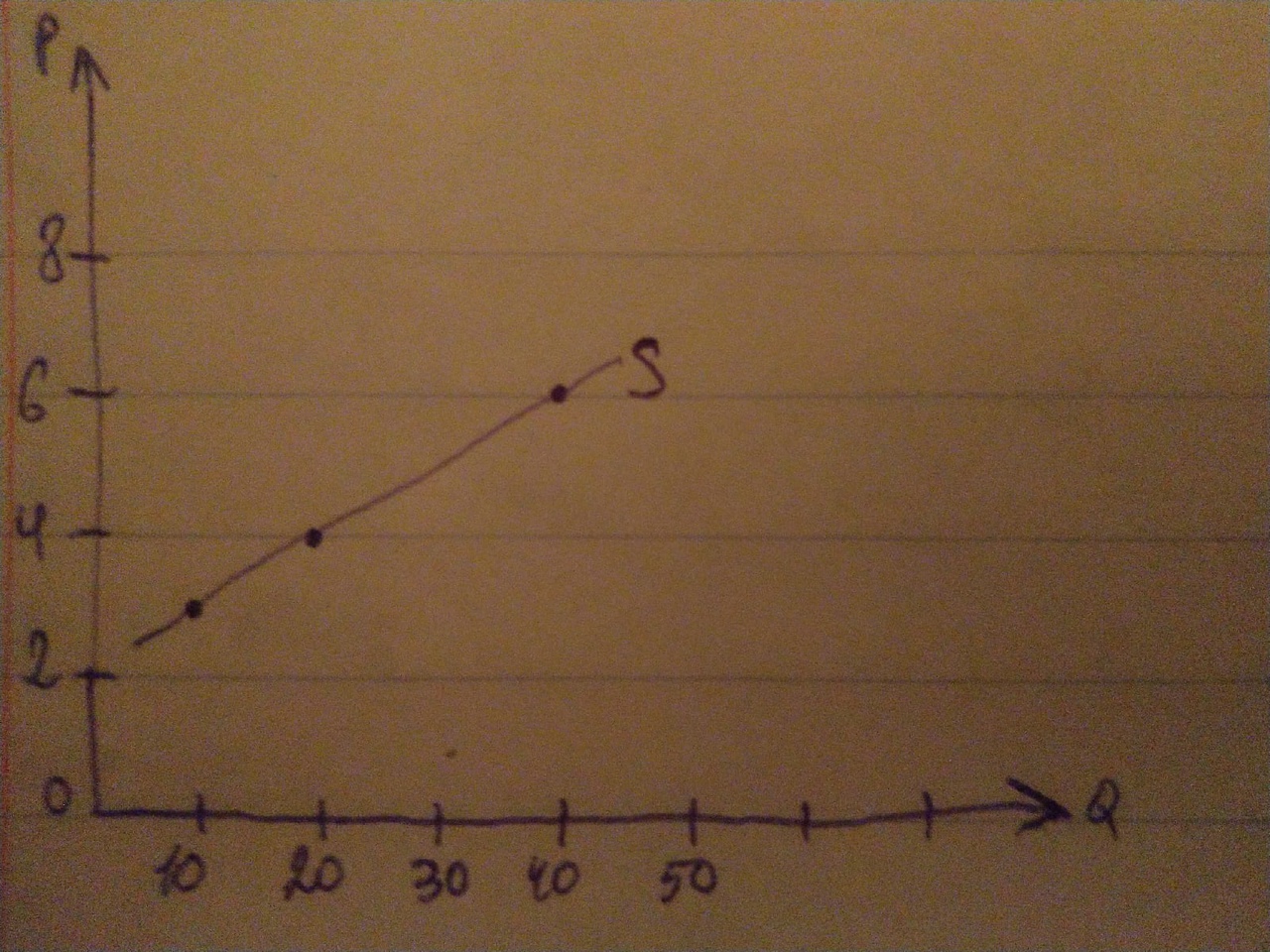 Задача 14. Функция предложения товара У задана формулой Qs = –100 + 20Р. Нарисуйте кривую предложения. Решение:
 Задача 15. В таблице представлены данные о ценах, объемах спроса и предложения товара Х. Начертите кривые спроса и предложения и определите равновесную точку.
Решение: В точке равновесия (Е) устанавливается равновесная цена 18 долл. и равновесный объём продаж 6 штук. 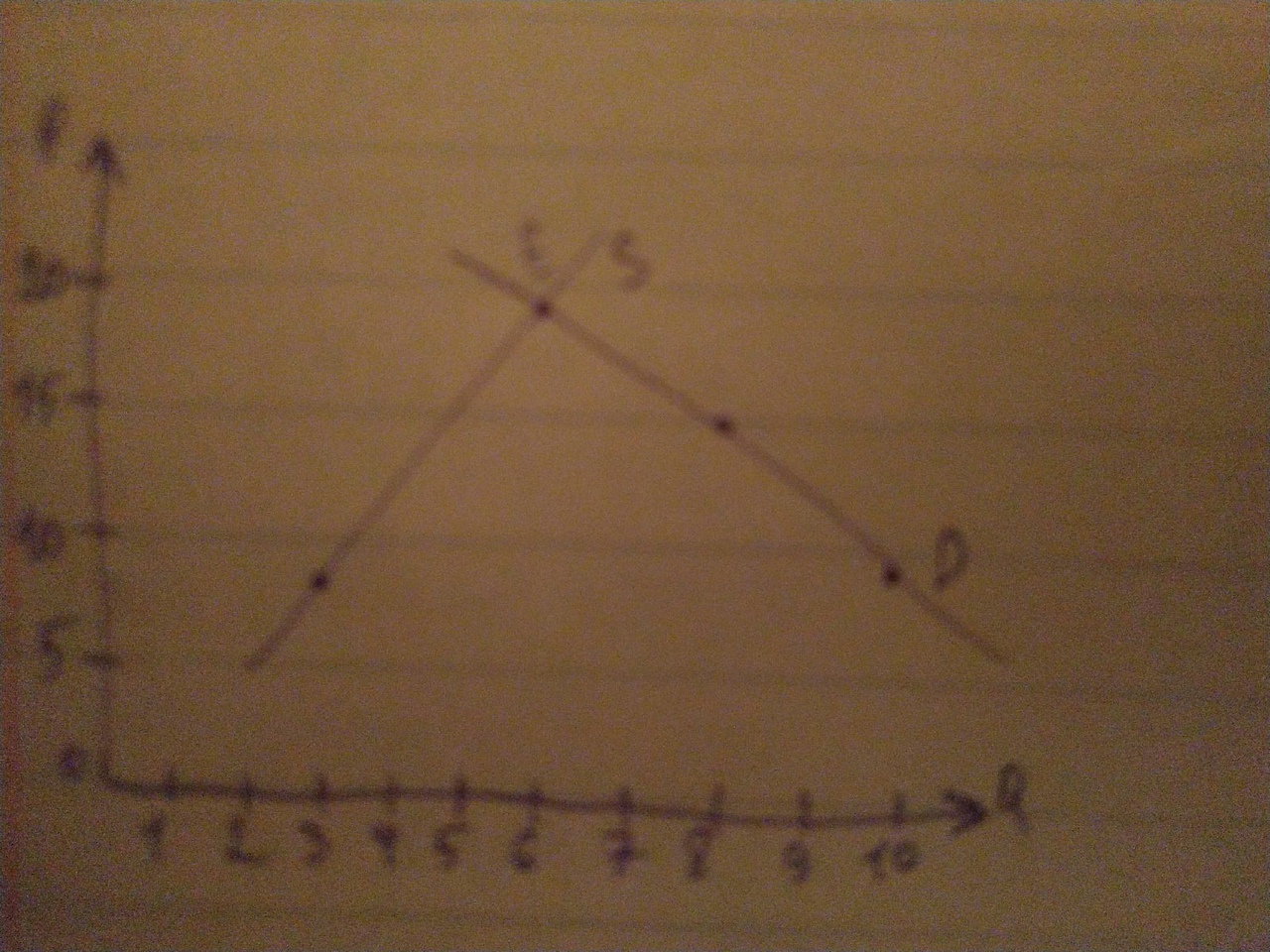 Задача 16. В таблице представлены данные о ценах, объемах спроса и предложения товара Х. Начертите кривые спроса и предложения и определите равновесную точку. Как изменится равновесие, если объем спроса увеличится на 2 единицы при каждом уровне цен.
Решение:  В точке равновесия устанавливается равновесная цена 18 долл. и равновесный объём продаж 26 штук. Если спрос увеличится, то кривая сдвинется вправо на две единицы. Новое равновесие установится при цене 20 долларов и объёме продаж 27 штук. Задача 17. Объем спроса на товар А на данном рынке определяется формулой Qd = 9 – Р, объем предложения – формулой Qs = –6 + 2Р, где Р – цена товара А. Найдите равновесную цену и равновесный объем продаж. Решение: В условиях равновесия объём спроса и объём предложения равны, следовательно, надо приравнять их формулы: 9 – Р = -6 + 2Р, отсюда, равновесная цена равна 5. Чтобы определить равновесный объем продаж, надо подставить равновесную цену в любую формулу: Qd = 9 – 5 = 4 или: Qs = -6 + 2*5 = 4. Задача 18. Функция предложения на говядину имеет вид: QD = 30 – P, где QD – величина спроса на говядину за день (кг), а Р – цена за один килограмм. Функция предложения описана следующим уравнением: QS = 15 + 2P, где QS – величина предложения за день (кг). построить графики спроса и предложения; найти равновесный объём и равновесную цену на мясо; какая ситуация возникнет на рынке мяса, если цена установится на уровне 3 ден.ед. за кг? Решить алгебраическим методом; найти эластичность спроса и предложения в точке равновесия. Решение: 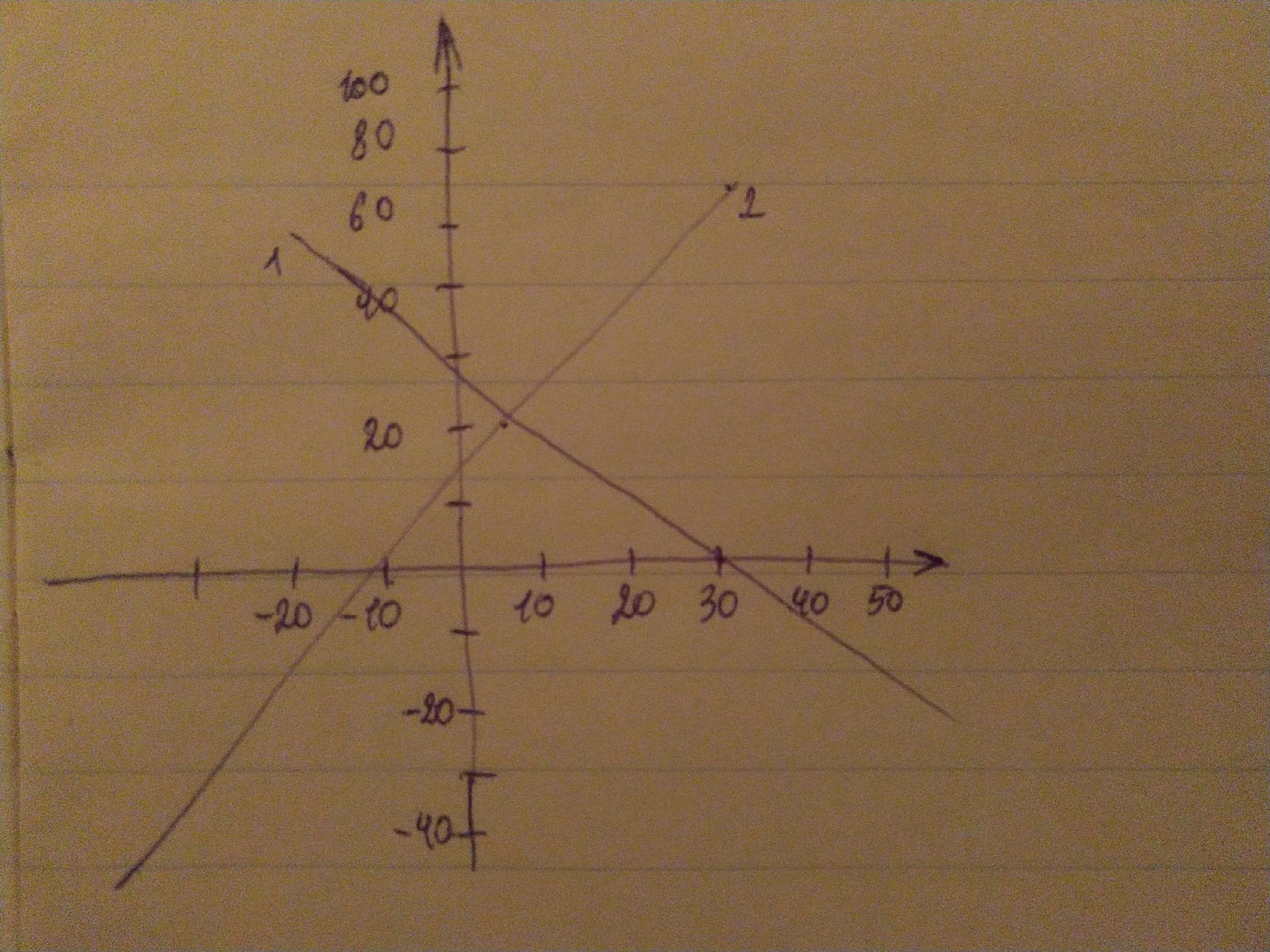 1. уравнения спроса и предложения – это уравнения линейных функций, для того чтобы их построить необходимо знать две точки. Р=0, QD = 30; QD = 10, Р=20 для графика спроса Р=0, QS = 15; QS = 20, Р=2,5 для графика предложения. 2. на графике равновесной цене и равновесному объёму соответствует точка пересечения графиков спроса и предложения Е(РЕ, QЕ). Очень часто графическим методом можно установить приблизительные значение, поэтому лучше использовать алгебраический метод: условие равновесия: QD = QS, или РD = РS следовательно: 30–Р=15+2Р 3Р=15 РЕ = 5 (ден.ед.) QD = 30-5=25 QS=15+2*5=25 QЕ=25 кг. 3. графический метод: при Р=3 ден.ед. : QD = 27 кг, QS=21 кг, дефицит товара равен 27-21=6 (кг). Алгебраический метод: подставим в уравнения спроса и предложения Р=3 ден.ед. QD = 30-Р=30 -3=27 QS=15+2Р=15+6=21 QD–QS=27-21=6 дефицит. 4. уменьшение предложения на 60% считается для каждой точки графика. Для этого необходимо составить таблицу значений.
Например: 15 – 100% Х – 60% 15*0,6=9 15-9=6 (кг) – новое предложение для Р=0 или 15*(1-0,6)=15*0,4=6 (кг). Аналогично необходимо сделать для каждой цены. Новый QS (кг) 15*0,4= 6 25*0,4= 10 35*0,4= 14 45*0,4= 18 5. РЕ = 5 (ден.ед), QЕ=25 кг. Эластичность спроса в точке (РЕ,QЕ) определяется формулой: выражение – производная функции QD = 30 – P, =(30 – P)'=-1 T = 1*5/25=0.2 – спрос неэластичный. Аналогично находится эластичность предложения: = 15+2З=2 Е = 2*5/25=0,4– предложение также неэластично. Издержки Задача 19. В таблице дана зависимость общих издержек предприятия от выпуска продукции.
Определите общие постоянные, общие переменные и предельные издержки. Решение: Общие постоянные затраты – это издержки, которые есть у предприятия, когда выпуск равен нулю, поэтому они равны 50. Поскольку они не меняются, то можно заполнить третью строчку. Общие переменные издержки – это разница между общими и общими постоянными затратами. Предельные издержки – это дополнительные затраты на выпуск дополнительной единицы продукции. Так как прирост продукции постоянно равен 1, то надо сопоставить общие затраты при приросте продукции: 90 – 50 = 40, 125 – 90 = 35 и т. д. Задача 20. На основе данных таблицы определите общие затраты, средние, средние постоянные, средние переменные, предельные издержки, если общие постоянные затраты равны 10:
Решение: Средние издержки определяются путем деления общих затрат на объем выпуска: 15 : 1 = 15, 22 : 2 = 11 и т. д. Средние постоянные затраты определяются по формуле TFC / Q, отсюда при Q = 1 все постоянные затраты войдут в издержки AFC = 10, при Q = 2 AFC = 10:2 = 5 и т. п. Средние переменные издержки определяются путем деления общих переменных затрат на объем выпуска: при Q = 1 AVC = TVC / Q = 5/1 =5; при Q = 2 AVC = 12/2 = 6. Предельные издержки – это дополнительные затраты на выпуск дополнительной единицы продукции. Так как прирост продукции постоянно равен 1, то надо сопоставить общие затраты при приросте продукции: 15 – 10 = 5, 22 – 15 = 7 и т. д. Задача 21. На основании данных таблицы определите средний и предельный продукт труда:
Решение: Средний продукт труда вычисляется по формуле: APL = TP / L Предельный продукт труда определяется по формуле: MPL = ΔTP / ΔL Задача 22. Заполните таблицу:
Решение: Задача 23. На основании данных таблицы определите оптимальный объем производства при цене 120 ден. ед.
Решение: Максимальная прибыль получается при выполнении условия МС=MR, т. е. при объеме, равном 6 ед. Рынок земли, капитала, труда, ценных бумаг Задача 24. Рыночная ставка аренды земли за сотку составляет 200 ден.ед. за год. Средний банковский процент по вкладам – 5% в год. Найти рыночную цену земли при отсутствии рисков и конъюнктурных колебаний. Решение: Цена земли (аренды)*100%/Банковский процент по вкладам=200*100%/5%=4000. Задача 25. Собственник акции с годовым дивидендом 25% решает её продать. Банковский процент равен 50%. По какому курсу будет продана акция? Решение: Курс акции = (дивиденд / банковский процент) *100% Курс акции = (25% / 50%)*100% = 50% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
