Микроэкономика. Курс лекций. Часть 1. Курс лекций Белгород 2009 удк 330. 101. 8 Ббк 65. 01 Э 59
 Скачать 3.33 Mb. Скачать 3.33 Mb.
|
|
Функция предложения – это функция, устанавливающая зависимость между величиной предложения и определяющими ее факторами. Она показывает максимальное количество блага, поставляемое на рынок при существующих условиях в данный момент времени. Функция предложения (как и спроса) может быть линейной и нелинейной. Так же, как и в случае со спросам, функция предложения будет включать свободный член а, а степень влияния каждой отдельного фактора будет отражаться коэффициентом b. Уравнение линейной функции имеет вид: QDх= a + bх·Рх+ ba·Рa+ br·Рr+ bI·I, где а – константа, показывающая минимальный объем производства блага (объем предложения при нулевой цене), a<0. При изменении величины а происходит сдвиг кривой предложения; b – коэффициент, показывающий реакцию величины предложения на изменение вышеперечисленных факторов. Воздействие каждого отдельного фактора на величину предложения будет неодинаково. Это найдет своеотражение в коэффициенте каждой переменной. Так коэффициент bх - коэффициент, показывающий реакцию величины предложения на изменение цены данного товара, будет положительной величиной (bх >0), поскольку между ценой данного блага и объемом предложения на него существует прямо пропорциональная зависимость. При изменении величины b изменяется наклон кривой. Если принять все неценовые факторы за постоянные, то функция предложения будет отражать зависимость величины предложения товара от изменения его цены и выглядеть следующим образом: QS= f(Px). Все продавцы стремятся получить на рынке самую высокую цену, чем выше будет цена, тем большее количество товара они готовы поставить на рынок, т.е. увеличить предложение. Например, при цене 10 руб. производитель готов продать 10 ед. блага, при цене 20 руб. – 30 ед., а при цене 30 руб. – 50 ед. блага. Графически эта зависимость называется кривой предложения (рис. 5.8).
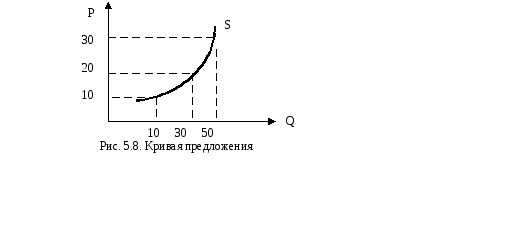 Кривая предложения имеет положительный наклон. Это объясняется действием закона предложения.
Если функция носит линейный характер, то графически кривая предложения представлена в виде наклонной прямой линии (рис. 5.9) и уравнение функции предложения будет представлено в виде: QS = а + b∙Р илиP = (1/b)∙Q - a/b. Уравнение показывает, что между рыночной (Р) и количеством продукции, которое производитель готов поставить на рынок (QS), существует прямая зависимость.  Характеризуя кривую предложения, следует учитывать, что пересечение кривой с осью абсцисс (0Х) на участке положительных значений, не означает, что производитель готов предоставить какое-то количество товаров бесплатно. Это будет отражать минимальный объем выпуска. Пересечение кривой предложения с осью ординат (0Y) указывает на ту минимальную цену, с которой производитель готов начать осуществлять предложение товара. Наклон кривой предложения будет отражать степень реагирования величины предложения на изменение цены: чем круче кривая, тем менее чувствительным к изменению цены будет производство. Наклон кривой предложения (также как и кривой спроса) равен отношению ∆P∕∆Q. Он будет постоянным на всем ее протяжении и идентифицирован в виде ценового коэффициента b, который является величиной обратной наклону кривой предложения: b = 1/(∆P∕∆Q)= ∆Q ∕∆Р. Аналогично спросу следует различать изменения предложения (функции предложения) и изменения объема предложения (величины предложения). Объем предложения меняется тогда когда изменяется только цена данного товара, а все остальные факторы, влияющие на предложение, неизменны. В этом случае говорят, что предложение не изменилось, мы движемся по (вдоль) кривой (рис. 5.10). Рост цен вызывает рост объема предложения и точку мы движем по кривой вверх (из точки А в точку В), снижение цен ведет к сокращению объема предложения и мы движем по кривой вниз из точки А в точку С. 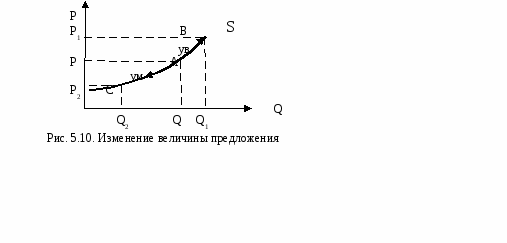 Изменение предложения (функции предложения), вызванное изменением неценовых факторов, при постоянной цене данного товара, всегда выражается в сдвиге кривой предложения влево или вправо. Увеличение предложения означает, что при данном уровне цены этого товара производители готовы продать больший объем товара, чем прежде. В этом случае кривая сдвигается вправо. Сокращение предложения означает, что при данном уровне цены этого товара производители готовы продать меньший объем товара, чем прежде. В этом случае кривая сдвигается влево (рис. 5 11). 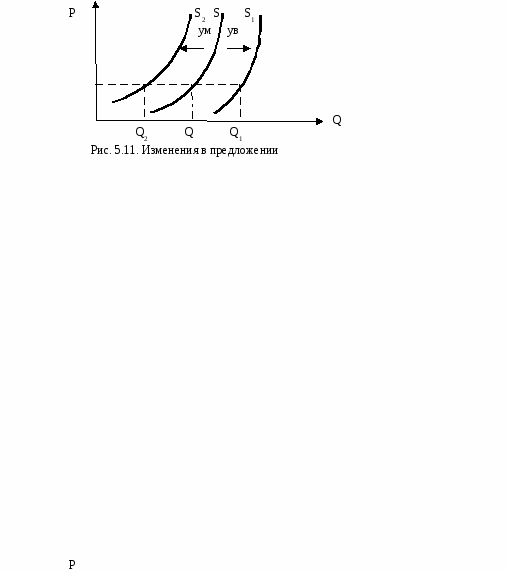 Например, главным фактором, воздействующим на предложение, являются издержки. Поэтому, если в результате достижений НТП или благоприятных погодных условий (если сельское хозяйство) удастся снизить издержки производства, то кривая предложения S сдвинется вправо в положение S1 при цене Р, в этом случае предложение возрастет. При повышении цен на факторы производства предложение сократится, то есть при цене Р объем предложения сократится до Q2, кривая сдвигается из положения S в положение S2. И, наоборот, в случае понижения цен на факторы производства произойдет увеличение предложения, кривая сдвинется в положение S1 . Таким образом, увеличение предложения означает, что при данном уровне цены производитель готов произвести и поставить на рынок больший объем товаров, чем прежде, кривая сдвигается вправо. Сокращение предложения означает, что при данном уровне цены производитель готов произвести и поставить на рынок меньший объем товаров, чем прежде, кривая сдвигается влево. 5.3. Рыночное равновесие Из выше изложенного следует, что потребитель стремится приобрести больше товаров по низкой цене, а производитель стремится поставить больше товаров по высокой цене. Как найти ту цену, которая устраивала бы покупателя и производителя? Для этого необходимо совместить кривую спроса и предложения. Кривые пересеклись в точке Е, в ней установилось равновесие (рис. 5.12). 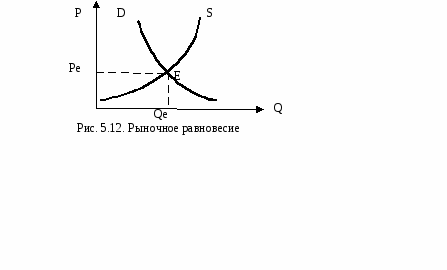 Равновесие – это такое состояние рынка, при котором для данного уровня цены объем рыночного спроса на благо равен объему предложения этого блага (QS= QD). Цена, при которой две кривые пересекаются, называется ценой равновесия (или равновесной ценой), а количество предлагаемого товара – равновесным объемом.
Равновесный объем – это объем, отражающий количество блага, при котором устанавливается равенство между ценой спроса Pdmax (максимальной ценой, которую потребитель готов заплатить за товар) и ценой предложения РS min (минимальной ценой, по которой товаропроизводитель готов поставить товар на рынок). Такое равновесие является выражением максимальной эффективности рыночной экономики, поскольку в состоянии равновесия рынок сбалансирован, ни у продавца, ни у покупателя нет внутренних стимулов к его нарушению. В результате установления равновесия выигрывает и потребитель, и производитель (рис. 5.13). Поскольку равновесная цена Ре ниже цены спроса, то выигрыш потребителя равен площади PdmaxEPe.
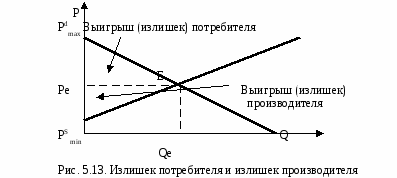 Выигрыш потребителя = ½∙(Рd max - Ре)∙Qе. Равновесная цена выше цены предложения, тогда выигрыш производителя равен площади PSminEPe. Выигрыш производителя = ½∙(Ре - РS min)∙Qе. К тому же выигрыш производителя - это разница между общей выручкой (TR=Pe∙Qe) и совокупными затратами на производство, равными площади 0PSminEQe.
Однако фактические (продажные) цены не всегда совпадают с равновесными, поскольку рынок не всегда находится в состоянии равновесия. Но он тяготеет к состоянию равновесия, то есть состояние рыночного равновесия имеет тенденцию к устойчивости. В подтверждении этого рассмотрим случаи нарушения рыночного равновесия. Допустим, что в результате действия различных рыночных сил цена отклонилась от равновесия и установилась ниже равновесной: Р1 < Pe (рис. 5.14),в этом случае объем спроса превышает объем предложения (0Q1D) > (0Q1S), товар станет дефицитным, так как при этой цене потребители не смогут купить столько товаров, сколько они хотели бы. Избыток спроса (Q1D-Q1S) будет оказывать давление на цену, в сторону повышения, потребители будут стараться обойти друг друга, чтобы купить имеющийся товар, а производители отреагируют на это повышением цен и расширением производства. В конечном счете, цена опять достигнет уровня Ре. Если же реальная цена оказалась выше равновесной Р2>Ре (рис. 5.14), производители пытаются изготовить и продать больше товаров, чем потребители готовы купить, т.е. предложение (0Q2S) превышает спрос (0Q2D), и на рынке образуется излишек (Q2S-Q2D) или избыток предложения. Что бы распродать этот избыток или не допустить его роста, производители начнут снижать цену. При уменьшении цены требуемое количество товара увеличится, а предполагаемое уменьшается до тех пор, пока не будет достигнута равновесная цена Ре.  Иной подход к объяснению механизма установления рыночного равновесия использовал А. Маршалл, который считал, что, реагируя на нарушение рыночного равновесия, продавцы маневрируют не ценой, а объемом предложения (рис. 5.15). При любом объеме производства, ниже равновесного (Qe<Q1), цена предложения меньше цены спроса (PS1<PD1). Это весьма выгодно для продавцов: выставив товары по цене спроса (PD1), они легко их реализуют, поскольку покупатели именно по этой цене готов приобрести именно это количество товара, получив огромную прибыль. Рост прибыли заставит фирму наращивать объемы производства. Предложение начнет расти, а цены будут сокращаться, пока не дойдут до равновесного уровня. 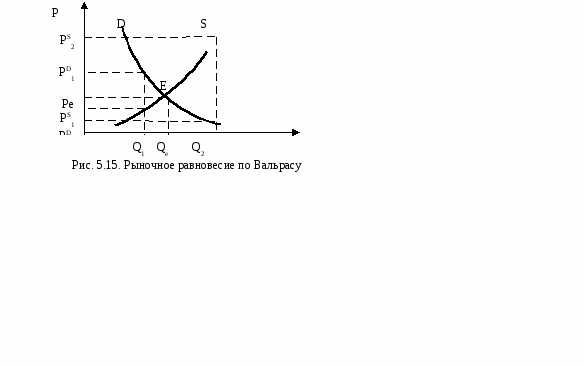 Если реальный объем производства выше равновесного (Qe> Q2), цена предложения будет выше цены спроса (PS2>PD2), то товары удастся продать только по цене спроса (PD2), то есть ниже себестоимости. Желающих производить товары по такой цене окажется немного. Предложение будет падать, пока не достигнет равновесного уровня. Цена при этом будет постепенно подниматься до равновесного уровня. Оба подхода к равновесию отражают рыночные реалии, причем, действие каждого из них проявляется в определенном временном интервале. Так, колебание цен (механизм Л. Вальраса) способствует установлению равновесия в краткосрочном периоде. Если товары уже произведены в определенном количестве, то приспособить объем предложения к размерам спроса возможно, лишь изменив цены. Таким образом, в модели Вальраса размеры производства заданы, а переменными оказываются цены. Изменение объема предложения (модель А. Маршалла) выступает на первый план в долгосрочном периоде. Поскольку только в долгосрочном периоде можно построить производственные мощности для удовлетворения любого объема спроса, главное, чтобы это принесло прибыль. В этих условиях именно цена становится главным ориентиром. В зависимости от того, насколько она привлекательна, производство либо наращивают, либо сокращают. Таким образом, в модели Маршалла, цена выступает как заданная, а предложение товаров окажется переменной величиной. Механизм равновесия можно также объяснить, используя иные модели, например, паутинообразную модель (рис. 5.16). Данная модель относится к числу динамических, поскольку учитывает фактор времени. Она рассматривает процесс формирования равновесия только в условиях, когда реакция участников сделок на изменяющиеся условия рынка растянута во времени. 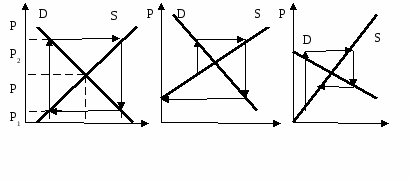 Q Q Q Q2 Qe Q1 а. Модель неустойчивого б. Модель неустойчивого в. Модель устойчивого равновесия равновесия равновесия Рис. 5.16. Паутинообразная модель
Возможно несколько вариантов: а) если угол наклона кривой предложения такой же, как и угол наклона кривой спроса |dP/dQS| =|dP/dQD| (рис. 5.16, а), то в такой ситуации равновесия никогда достигнуто не будет, т.к. происходит постоянное колебание цен относительно равновесной. Если цена установилась ниже равновесной, то на рынке образуется дефицит (Q1Q2), который приведет к росту цен до Р2. При цене Р2 производи-тели увеличивают выпуск продукции, а потребители снижают объем покупок, образовавшиеся излишки способствуют снижению цены; б) если угол наклона кривой спроса круче угла наклона кривой предложения |dP/dQS|<|dP/dQD| (рис. 5.16, б), то равновесие не наступает. Цена с каждым разом опускается все ниже и ниже, в такой ситуации производство прекращается или не растет. Происходят расширяющиеся колебания цен: от одного периода к другому цены все более удаляются от цены равновесия; в) если угол наклона кривой предложения круче угла наклона кривой спроса |dP/dQS|>|dP/dQD| (рис. 5.16, в), то объем производства и цена все более приближается к уровню равновесия. Происходит сужающее колебание цен. Однако паутинообразная модель применима лишь к определенной продукции, она не учитывает влияние неценовых факторов, смещающих кривые. Увеличение спроса (рис. 5.17) приводит к смещению кривой спроса из положения D в положение D1, в результате равновесие смещается в точку Е1, это приводит к росту равновесной цены (Ре1>Ре) и равновесного объема (Qe1>Qe). Снижение спроса вызывает смещение кривой спроса влево в положение D2, а это вызывает уменьшение равновесной цены (Ре<Pe2) и равновесного объема (Qe2<Qe). 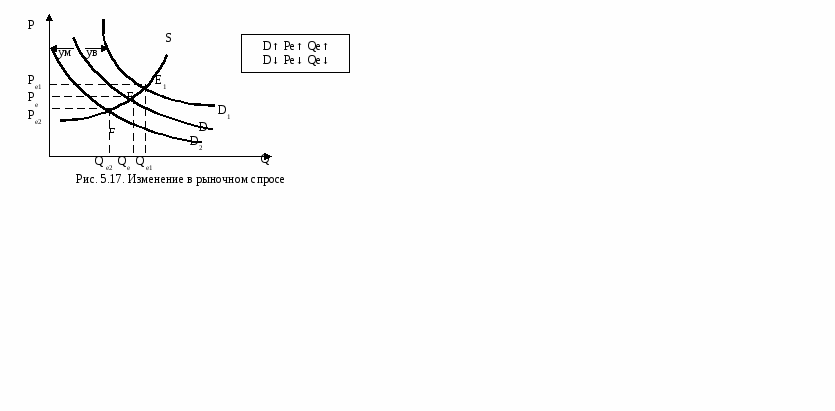 Уменьшение предложения (рис. 5.18) вызовет смещение кривой S в положение S1, в результате равновесие сместится из точки E в точку E1, вызывая увеличение равновесной цены до Ре1 и снижение равновесного объема Qe1. Увеличение же предложения вызовет смещение кривой S в положение S2, что приведет к увеличению равновесного объема до Qe2 и уменьшению равновесной цены до Ре2. 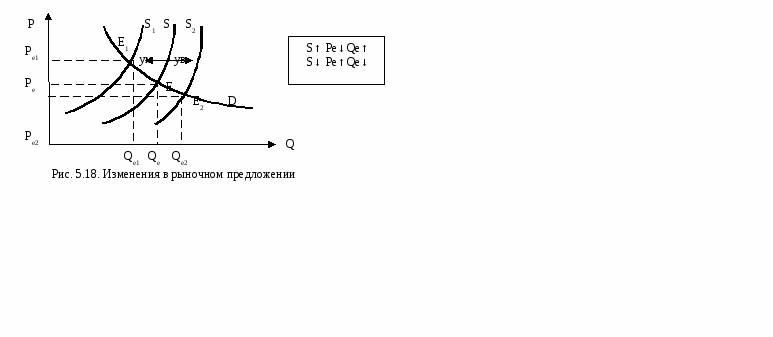 Возможна ситуация одновременного изменения спроса и предложения (рис. 5.19). Например, установилась жаркая погода, одновременно из-за перегрузки выходят из строя две линии на местном хладокомбинате. В результате жаркой погоды спрос на мороженое возрос. Р D1 S1 S ув D ум Ре1 Е1 Ре’ Е’ Ре Е Q1=Qe Qe′ Рис. 5. 19. Изменение рыночного спроса и предложения 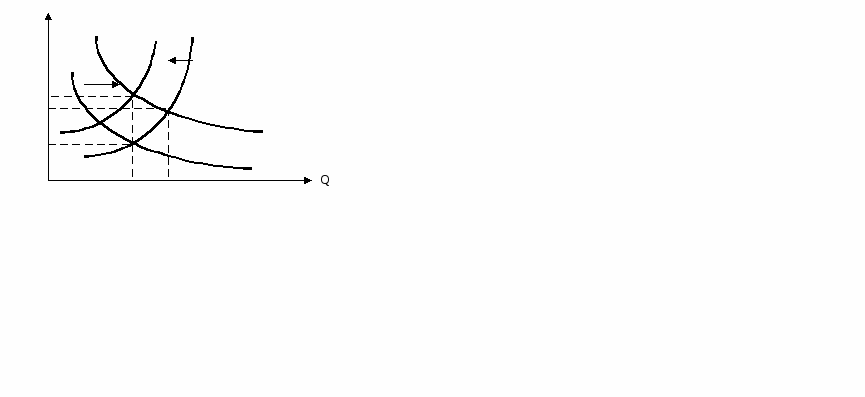 Кривая Dсместилась в положение D1, установилось промежуточное равновесие в точке E’, это привело к росту равновесной цены до Р’ и равновесного объема до Q’. Но из-за перегрузки вышли из строя две линии, следовательно, предложение уменьшилось. Кривая S сместилась влево в положение S1, в результате новое равновесие установилось в точке E1, в результате возросла цена до Ре1 и изменился равновесный объем Q1. В нашем случае от снизился до прежнего - Qe. Изменение объема будет зависеть от наклона кривых. 5.4. Эластичность спроса и предложения Важную роль в изучении возможных реакций со стороны экономических агентов на изменения цены играет понятие эластичности. Эластичность показывает степень реакции одной величины на изменения другой, например, изменение объема спроса в связи с изменением цены. Такая реакция может быть слабой или сильной, и, естественно, будут менять свою форму кривые спроса и предложения. Знакомство с аппаратом эластичности начнем с эластичности спроса. Эластичность – безразмерная величина, значение которой не зависит от того, в каких единицах мы измеряем цены, объем или другие величины.
Различают эластичность спроса по цене, эластичность спроса по доходу и перекрестную эластичность. Эластичность спроса по цене.
На рис. 5.20 представлены две кривые спроса, в первом случае изменения цены с 7 до 4 руб. не привело к резкому увеличению спроса (εd = 0,3), во втором случае спрос резко возрос (εd = 1,22). 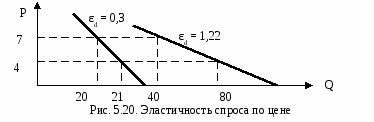 Спрос называется неэластичным, если при изменении цены объем спроса изменяется незначительно. Спрос на товар называют эластичным, если при изменении цены объем спроса существенно изменяется. Итак, эластичность спроса по цене (εрd) показывает степень воздействия изменения цены на изменение количества продукции, на которую предъявлен спрос. Эластичность определяется как отношение процентного изменения объема спроса к процентному изменению цены. Коэффициент эластичности спроса по цене, как правило, является отрицательной величиной, так как с ростом цены объем спроса падает, но в экономической теории принято пользоваться абсолютным значением этого показателя, поэтому знак «минус» порой не ставят, но при расчетах принимают во внимание.
Например, εРd=-2. Это означает, что снижение цены (рост) на 1% приводит к росту (снижению) объема спроса на 2%. Эластичности взаимно обратных функций являются взаимо-обратными величинами: εРd=1/ εdР , где εРd- коэффициент эластичности спроса по цене, εdР - коэффициент эластичности цены по спросу. Поясним вышеизложенное на примере. Пусть эластичность спроса по цене равна -0,6 (снижение цены на 1% приведет к росту объема спроса на 0,6%). Определим коэффициент эластичности цены по спросу: εdР=1/ εРd= 1/-0,6= -1,66. εdР = -1,66 – это означает, что рост объема спроса на 1% приведет к сокращению цены на 1,66% Эластичность линейной функции спроса изменяется от 0 до -∞. Различают пять типов эластичности:
На степень эластичности спроса влияет целый ряд факторов: 1) наличие заменителей: чем больше товаров–субститутов, тем эластичней спрос на данный товар; 2) удельный вес товара в бюджете потребителя: чем выше удельный вес, тем выше ценовая эластичность; 3) размер дохода; 4) вид товара: является ли товар предметом роскоши (спрос на такие товары эластичен) или предметом первой необходимости (спрос на них неэластичен); 5) размер запаса: чем больше запас, тем более эластичен спрос; 6) рассматриваемый период: в краткосрочном периоде благо неэластично, в долгосрочном - эластично. Например, в краткосрочном периоде потребеление электроэнергии неэластично, так как мы не можем быстро отказаться от имеющихся электроприборов, а в долго-срочном - довольно эластично, поскольку мы будем заменять электро-емкие приборы более экономичными. Различают точечную и дуговую эластичность. При небольших изменениях цены или объема спроса или в случае вычисления эластичности в конкретной ситуации (точке) используется формула точечной эластичности, а при значительных – дуговой эластичности. Дуговая эластичность – это показатель средней реакции объема спроса на изменение цены товара на некотором отрезке D1D2 (рис. 5.21). Ее определяют с учетом средней точки. 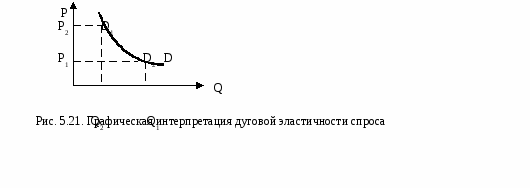 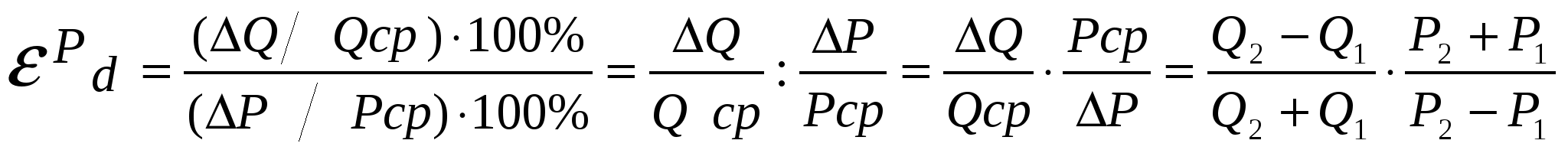 . .Точечная эластичность характеризует относительное изменение одного фактора, например объема спроса, при бесконечно малом изменении другого, например цены. Для ее расчета используют слудеющие формулы: 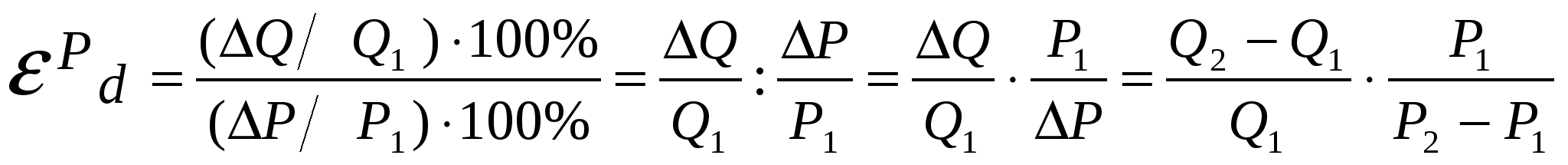 , ,или, взяв производную от функции спроса: 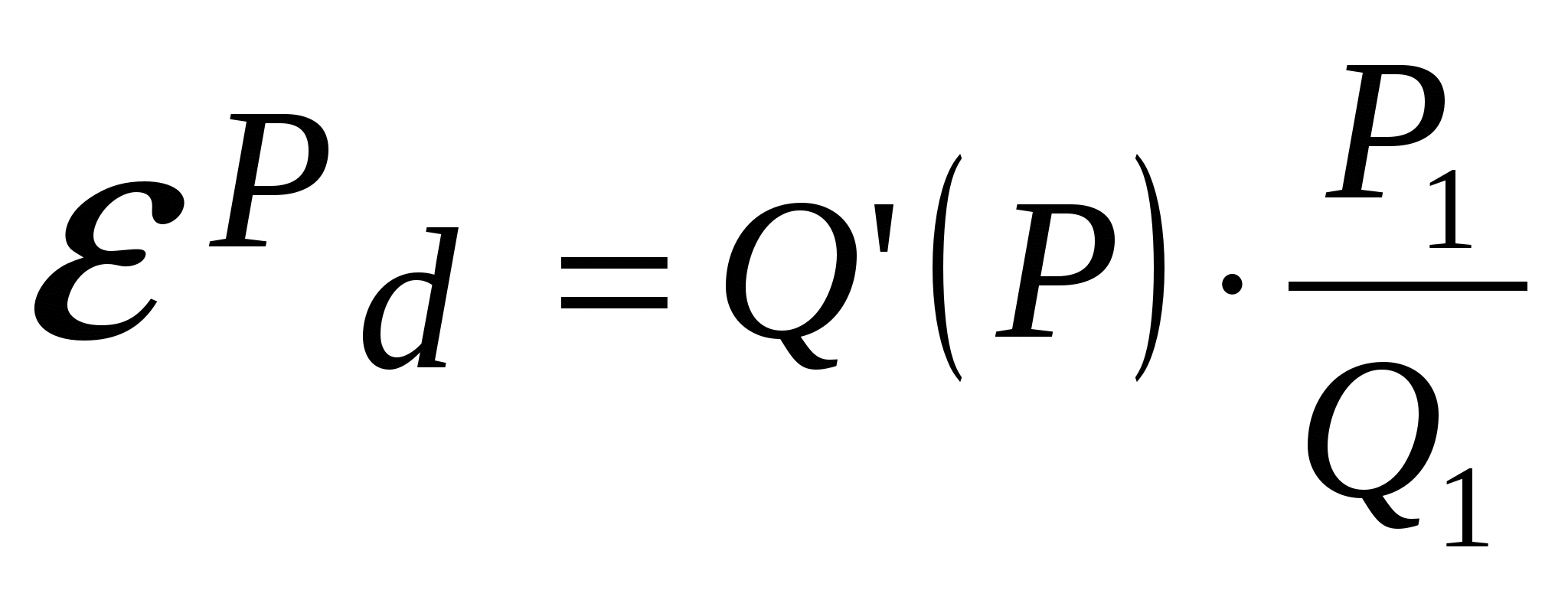 , ,где Q’(P) – производная функции спроса по цене, Р1 – цена в конкретной точке, Q1 – объем спроса в конкретной точке. Точечную эластичность можно определить и графическим способом, если провести касательную к кривой спроса в искомой точке. Наклон кривой спроса в любой точке определяется значением тангенса угла касательной с осью 0Х (рис. 5.22). Ошибочно считают, что значение точечной эластичности обратно пропорционально тангенсу угла наклона α, в формуле точечной эластичности только значение (∆Q/∆P) обратно пропорционально тангенсу угла наклона α. ∆Q/∆P = -tgα, тогда tg α =∆Р/∆Q. 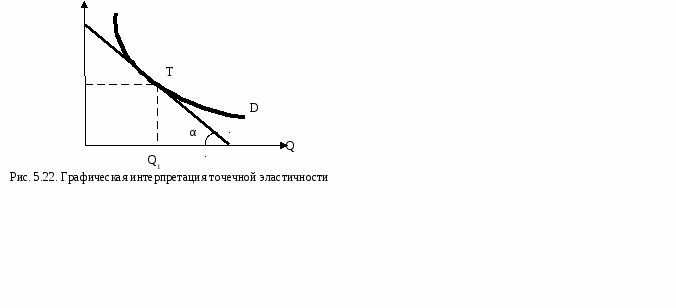 Р Р1 Наклон кривой спроса будет постоянным на всем ее протяжении и идентифицирован в виде ценового коэффициентаb (кривая спроса задается линейной функцией QD = a - b∙P), который является величиной обратной наклону кривой спроса, т.е. b = 1/(∆P∕∆Q)= ∆Q ∕∆Р. Подставим это выражение в классическую формулу точечной эластичности и получим: 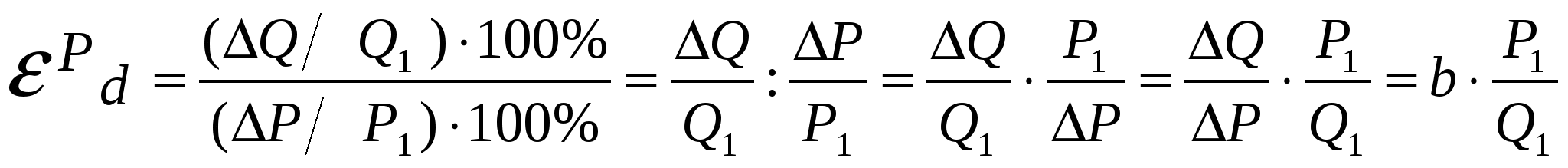 . .Перекрестная эластичность. Спрос на товар зависит также и от цен на другие товары.
Коэффициент перекрестной эластичности спроса представляет собой отношение изменения объема спроса на товар ί к вызвавшему его изменению цены на товар ј: 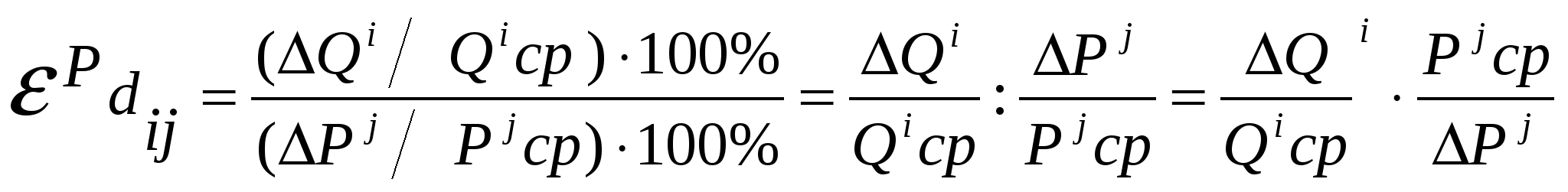 . .Различают дуговую и точечную перекрестную эластичность. Дуговая эластичность - это показатель средней реакции объема спроса одного товара на изменение цены на другой товар на некотором отрезке. 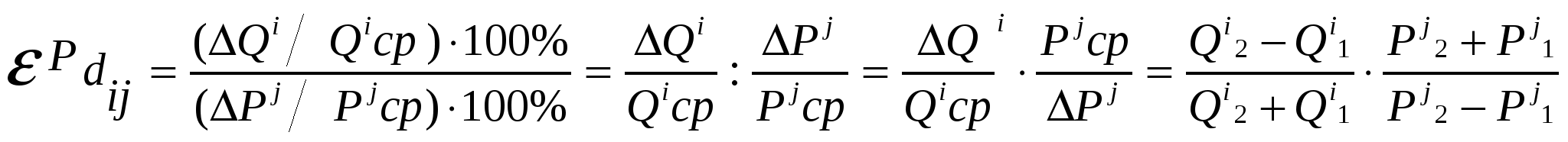 . .Точечная эластичность характеризует линейную зависимость между ценой одного товара и объемом спроса на другой. Для ее расчета используют следующую формулу: 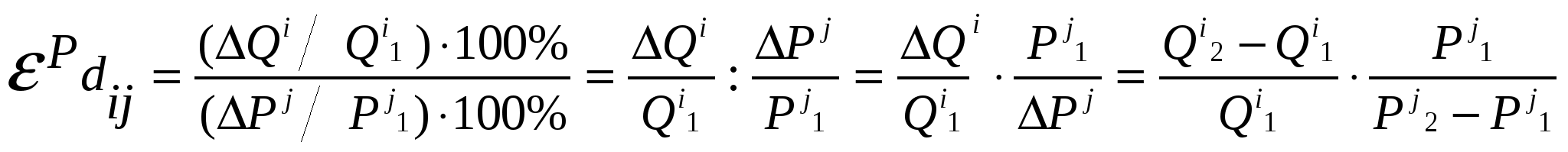 . .Коэффициент перекрестной эластичности может быть как положительной, так и отрицательной величиной (рис. 5.23), он указывает на тип взаимосвязи благ, то есть его абсолютное значение отражает степень этой взаимосвязи. Чем выше перекрестная эластич-ность спроса, тем выше степень заменяемости благ, чем меньше вели-чина перекрестной эластичности, тем больше взаимодополняемость благ.  Это важно для разработки общей и ценовой с тратегии организаций, поскольку следует принимать во внимание не только возможность конкуренции товаров-субститутов (заменяемых товаров), но и наличие и ценовые тенденции взаимодополняемых товаров (например связаны между собой рынок жилья и рынок строительных материалов, рынок автомобилей и рынок автомобильного топлива). Блага взаимозаменяющие (рис. 5.23 а): 0 < εРdij < ∞. Коэффициент перекрестной эластичности будет положительной величиной и изменяться в пределах от 0 до ∞. Это означает, что при изменении цены на благо j спрос на благо i изменится в том же направлении. Например, снижение цены на благо j вызовет снижение спроса на благо i и наоборот. Взаимодополняемые блага (рис. 5.23 б): εРdi < 0. Коэффициент перекрестной эластичности будет отрицательной величиной. Это означает, что при изменении цены на благо j спрос на благо iизменяется в противоположном направлении. Например, снижение цены на благо jвызовет рост спроса на благо i, и наоборот. Блага, независящие друг от друга в потреблении (рис. 5.23 в) имеют нулевую перерестную эластичность, то есть рост цен на один товар никак не связан ни с потребелнием, ни с изменением спроса на другой товар. Практическая значимость эластичности спроса состоит в том, что различные случаи эластичности непосредственно влияют на получаемую выручку производителем (TR) и расходы потребителей. TR = P∙ Q, где Р- цена данного товара, Q – количество купленного товара. З начение эластичности будет различным в разных точках кривой (рис. 5.24). 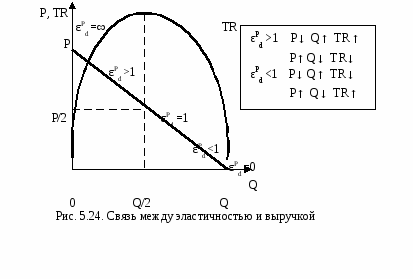 Эластичность линейной функции спроса изменяется от 0 (в точке пересечения кривой линейной спроса и осью абсцисс) до ∞ (в точке пересечения кривой линейной спроса и осью ординат). Если спрос по цене эластичный(εРd >1), то снижение цены вызовет рост выручки (поскольку незначительное снижение цены приведет к большему в процентном выражении росту объема спроса). Рост цены вызовет сокращение выручки (поскольку незначительное повышение цены приведет к большему в процентном выражении сокращению объема спроса). Если спрос по цене неэластичен (εРd<1), то снижение цены приведет к падению выручки. Рост цен вызовет рост выручки. В средине отрезка 0Q получим единственную точку на линейной кривой спроса с единичной эластичностью, в которой выручка максимальна и неизменна при любом изменении цены. В этом случае повышение доходности и рентабельности производства возможно за счет неценовых факторов. |