Финансовый менеджмент. Курс лекций "Основы финансового менеджмента"
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
5.5. Количественное измерение риска Средняя арифметическая ожидаемых доходностей (ri) инвестиций, взвешенная по вероятности возникновения отдельных значений, называется математическим ожиданием. Условимся называть эту величину средней ожидаемой доходностью: , (5.5.1) где pi – вероятность получения доходности ri. В статистике количественным измерителем степени разброса значений переменной вокруг ее средней величины (математического ожидания) является показатель дисперсии (σ2): (5.5.2) Квадратный корень из дисперсии называется средним квадратическим или стандартным отклонением σ: (5.5.3) Данный показатель используется в финансовом менеджменте для количественного измерения степени риска планируемых инвестиций. Чем больше разброс ожидаемых значений доходности вложений вокруг их среднеарифметической величины, тем выше риск, сопряженный с данным вложением. Фактическая величина доходности может быть как значительно выше, так и значительно ниже ее средней величины. Практическая ценность такого подхода заключается не только (и не столько) в применении статистических формул, а в осознании необходимости многовариантного планирования инвестиционных решений. Любые ожидаемые результаты этих решений могут носить лишь вероятностный характер. От финансиста требуется не только правильно применить формулу расчета доходности инвестиций, но и дать количественную оценку вероятности возникновения конкретного результата. Как минимум, необходимо планировать не менее трех вариантов развития событий: оптимистический, пессимистический и наиболее вероятный. Полная вероятность возникновения всех этих вариантов должна быть равна 1. Например, оценивая две акции А и Б, инвестор пришел к выводу, что распределение вероятностей их ожидаемой доходности можно представить следующим образом: Таблица 5.5.1 Распределение вероятностей доходности акций
Среднеарифметическая ожидаемая доходность (математическое ожидание), взвешенная по вероятности каждого варианта составит: для акции А ; для акции Б . То есть, с точки зрения ожидаемой доходности инвестору безразлично, какую именно акцию приобрести – любая из них должна принести ему 15% дохода. Однако, данная логика рассуждений ошибочна. Прежде всего инвестор должен оценить величину риска, сопряженного с каждым из сравниваемых активов. Для этого ему следует рассчитать стандартные отклонения доходности σ по каждой ценной бумаге. Выполним эти расчеты в табл. 5.5.2: Таблица 5.5.2 Расчет среднего квадратического отклонения
Разброс значений ожидаемой доходности по акции А почти в 20 раз больше, чем по акции Б. Очевидно, что первое вложение является более рискованным, поэтому предлагаемая по нему компенсация риска в виде 15%-ой доходности абсолютно недостаточна. Точно такую же среднюю ожидаемую доходность способна принести менее рискованная акция Б. Схема на рис. 5.5.1 наглядно иллюстрирует разброс ожидаемых значений доходности по двум акциям: он значительно шире по первому активу (А).На этой схеме изображено распределение вероятностей. В данном случае оно является дискретным, прерывистым, поэтому данные представлены в форме столбцов (гистограмма). В случае непрерывного распределения, график представляет собой плавную кривую. Тесноту связи двух переменных в статистике измеряют при помощи коэффициентов корреляции, которые рассчитываются по формуле: , (5.5.4) где Cov(А, Б) – коэффициент ковариации между доходностью акций А и Б. Коэффициент ковариации вычисляется по формуле: (5.5.5) Использовав данные табл. 5.5.2, получим: Тогда коэффициент корреляции составит: 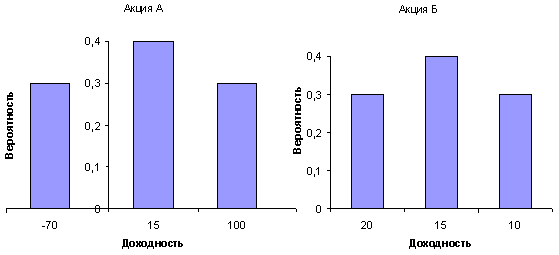 То есть, “поведение” акций на рынке абсолютно идентично, поэтому они не могут быть использованы для диверсификации несистематического риска инвестиционного портфеля. С увеличением стоимости акции А будет возрастать в цене и акция Б, соответственно падение цены на первую акцию обусловливается влиянием тех же факторов, что и на вторую. В случае положительного влияния факторов, инвестор будет богатеть значительно быстрее, однако в противоположном случае, его убытки также будут возрастать опережающими темпами. 5.6. Модель оценки финансовых активов (CAPM) Наряду с доходностью ценных бумаг или их портфелей, может быть определена доходность конкретного финансового рынка (например NYSE) в целом. Для этого можно использовать изменение какого-либо фондового индекса (DJIA, S&P 500 и т.п.). Прирост (снижение) этого индекса за определенный период должен быть отнесен к значению индекса на начало периода: , где (5.6.1) I1, I0 – значения фондовых индексов соответственно на конец и начало периода; rm – уровень доходности рынка в целом. Например, фактическое значение индекса S&P 500 составило на 10 мая 2000 года 1384,29, на следующий день оно достигло уровня 1401,74. Темп прироста за день (дневная доходность “средней” акции) равен 1,26%. Аннуилизировав этот результат по ставке простых процентов (временная база – 366 дней), получим: Полученный гигантский результат отражает изменение индекса лишь за 1 день, поэтому его не стоит автоматически экстраполировать на все остальные дни года. Безусловно, рост курса акций будет чередоваться с его падением, в результате чего фактическая годовая доходность “средней” акции будет иметь гораздо более скромную величину. В табл. 5.6.1 приведена динамика фактической годовой доходности индекса S&P 500 за ряд лет в сопоставлении с динамикой доходности одной отдельно взятой акции, обращающейся на этом же рынке. Таблица 5.6.1
Приведенные в таблице данные позволяют сопоставить между собой изменения доходности отдельной акции и доходности рынка в целом. Если в предыдущем параграфе находилась теснота связи между отдельными акциями, входящими в инвестиционный портфель, то теперь можно найти степень зависимости доходности одной акции от уровня прибыльности всего рынка. В статистике подобные задачи решаются путем построения регрессионных уравнений вида: , где (5.6.2) y – результативный показатель; x – влияющий фактор; - свободный член уравнения регрессии; – коэффициент регрессии; – погрешность. Важнейшим параметром этого уравнения является коэффициент регрессии , который показывает, насколько сильно изменение факторного показателя x влияет на результирующий признак y. В случае линейной формы регрессионного уравнения, простейшим способом оценки его параметров является использование метода наименьших квадратов, заключающегося в решении относительно : и следующей системы линейных уравнений: 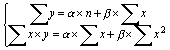 , где (5.6.3) , где (5.6.3) n – общее число наблюдений (лет). Решив ее, получим: Значение коэффициента регрессии β = 0,27 показывает, что с увеличением средней доходности рынка на 1 процентный пункт, доходность данной ценной бумаги возрастет лишь на 0,27 пункта. Иными словами, акция подвержена относительно менее сильному воздействию рыночных колебаний: при снижении рыночной доходности на 1 пункт, падение доходов по этой акции также составит в среднем лишь 0,27 пункта. Графическая аппроксимация фактических данных линейной функцией представлена на рис. 5.6.1. Коэффициент регрессии β представлен на нем углом наклона линии регрессии к оси абсцисс. 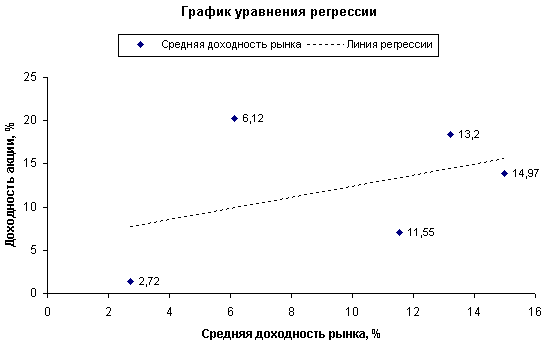 Рисунок 5.6.1. Графическое представление взаимосвязи между доходностью отдельной акции и средней рыночной доходностью Таким образом, коэффициент регрессии β служит количественным измерителем систематического риска, не поддающегося диверсификации. Ценная бумага, имеющая β-коэффициент, равный 1, копирует поведение рынка в целом. Если значение коэффициента выше 1, реакция ценной бумаги опережает изменение рынка как в одну, так и в другую сторону. Систематический риск такого финансового актива выше среднего. Менее рисковыми являются активы, β-коэффициенты которых ниже 1 (но выше 0). Концепция β-коэффициентов составляют основу модели оценки финансовых активов (Capital Assets Pricing Model, CAPM). При помощи этого показателя может быть рассчитана величина премии за риск, требуемой инвесторами по вложениям, имеющим систематический риск выше среднего. Формула определения требуемой инвесторами доходности финансового инструмента имеет вид: , где (5.6.4) rf – безрисковый уровень доходности (risc free). Считается, что инвесторы питают неприязнь к излишнему на их взгляд риску (risc aversion), поэтому любая ценная бумага, отличная от безрисковых государственных облигаций или казначейских векселей, может рассчитывать на признание инвесторов только в том случае, если уровень ее ожидаемой доходности компенсирует присущий ей дополнительный риск. Данная надбавка называется премией за риск (второе слагаемое в формуле 5.6.4), она напрямую зависит от величины β-коэффициента данного актива, так как предназначена для компенсации только систематического риска. Несистематический риск может быть устранен самим инвестором путем диверсификации своего портфеля, поэтому рынок не считает нужным устанавливать вознаграждение за этот вид риска. Сама по себе CAPM является изящной научной теорией, имеющей солидное математическое обоснование. Для того, чтобы она “работала” необходимо соблюдение таких заведомо нереалистических условий как наличие абсолютно эффективного рынка, отсутствие транзакционных издержек и налогов, равный доступ всех инвесторов к кредитным ресурсам и др. Тем не менее столь абстрактное логическое построение получило практически всеобщее признание в мире реальных финансов. Крупнейшие рыночные институты, такие как инвестиционный банк Merril Lynch, регулярно рассчитывают β-коэффициенты всех крупных компаний, котирующихся на фондовых биржах. Отсутствие в России сформированной финансовой инфраструктуры пока еще препятствует использованию всего потенциала, заложенного в данную модель. Поэтому рассмотрим пример  Рисунок 5.6.2. Взаимосвязь уровня β-коэффициента и требуемой доходности расчета уровня ожидаемой доходности с использованием подхода capm на фондовом рынке сша. Компания, имеющая β-коэффициент 2,5, собирается привлечь дополнительный собственный капитал путем эмиссии обыкновенных акций. Уровень безрисковой процентной ставки составляет 6,25%, средняя доходность рынка, рассчитанная по индексу S&P 500, – 14%. Для того, чтобы сделать свои ценные бумаги привлекательными для инвесторов, компания должна предложить по ним ежегодный доход не ниже 25,625% (6,25 + 2,5 * (14 – 6,25)). Размер премии за риск составит 19,375%. Столь существенные ограничения, накладываемые рынком на возможности снижения цены капитала, устанавливают предел доходности инвестиционных проектов, которые компания собиралась финансировать привлекаемым капиталом: внутренняя норма доходности этих проектов должна быть не ниже 25,625%. В противном случае NPV проектов окажется отрицательной, то есть они не обеспечат увеличения стоимости предприятия. Если бы β-коэффициент компании был равен 1,5, то размер премии за риск составил бы 11,625% (1,5 * (14 – 6,25)), то есть цена нового капитала составила бы лишь 17,875%. Полученные результаты могут быть представлены на графике, показывающем зависимость требуемой инвесторами нормы доходности при заданных значениях β-коэффициента, безрисковой процентной ставки (rf) и средней рыночной доходности (rm). Данный график отражает линию рынка ценных бумаг (Security Market Line, SML) (рис. 5.6.2). Использование CAPM дает финансовому менеджеру инструмент прогнозирования издержек по привлечению нового капитала для реализации инвестиционных проектов. Финансы любого предприятия являются открытой системой, поэтому, планируя свои капиталовложения, оно обязано учитывать при этом конъюнктуру финансового рынка. Менеджеры компании могут абсолютно ничего не знать об индивидуальных особенностях и личных предпочтениях потенциальных инвесторов. Это не освобождает их от обязанности предугадать главную потребность любого инвестора – получить доход, компенсирующий риск инвестиций. В этом им может помочь использование модели оценки финансовых активов. 5.7. Финансовый леверидж Понимание природы инвестиционного риска и умение оценивать его величину важно не только для инвестора, но и финансового менеджера предприятия. Величина β-коэффициента конкретной компании служит для инвестора ориентиром при определении им уровня желаемой доходности по ценным бумагам этой компании. Для финансового менеджера ставка выплачиваемого дохода означает цену привлечения капитала. Поэтому, планируя источники финансирования инвестиций, он обязан учитывать рыночную оценку риска своей компании. В противном случае параметры доходности эмитируемых ценных бумаг окажутся выше или ниже тех, которые могли быть одобрены рынком. А это будет означать или непомерно высокую цену нового капитала или невозможность разместить ценные бумаги из-за их низкой доходности. Риск конкретной ценной бумаги интересует инвестора только как фактор изменения общего риска портфеля. При необходимости данный риск может быть диверсифицирован, если этого окажется недостаточно, инвестор может просто избавиться от слишком рискованной на его взгляд бумаги. Финансовый менеджер находится в качественно иной ситуации – весь его “портфель” состоит из одного только предприятия, избавиться от которого он может лишь потеряв свою работу. Он обязан четко представлять причины, обусловившие ту или иную рыночную оценку риска, присущего данной компании. Как видно из схемы на рис. 5.4.1 (параграф 5.4), наряду с внешними факторами (валютный риск, риск процентной ставки и др.), существуют внутренние предпосылки увеличения или снижения риска предприятия: предпринимательский (деловой) и финансовый риски. Под предпринимательским понимается риск неполучения операционной прибыли (прибыли до уплаты процентов по кредитам и налога на прибыль). Одной из характеристик этого риска является операционный леверидж, рассмотренный в параграфе 3.2. Финансовый риск сопряжен с возможностью неполучения чистой прибыли до уплаты налога на прибыль, но после выплаты процентов. Одним из измерителей риска такого рода является финансовый леверидж или эффект финансового рычага. Сравнив между собой формулы определения операционной прибыли и чистой прибыли до налогообложения, можно сделать вывод, что дополнительным фактором риска в случае финансового левериджа выступает общая сумма процентов за кредит: (5.7.1) , где (5.7.2) Приб – операционная прибыль; E-I – чистая прибыль до уплаты налога на прибыль; p – цена 1 изделия; v – переменные издержки на 1 изделие; q – объем продаж; FО – фиксированные расходы, связанные только с операционной деятельностью (без процентов за кредит); I – сумма процентов за кредит. Очевидно, что сумма процентных платежей увеличивается по мере роста удельного веса заемного капитала в общей структуре источников финансирования предприятия. Следовательно, финансовый леверидж отражает степень зависимости предприятия от кредиторов, то есть величину риска потери платежеспособности. Чем выше финансовый леверидж, тем выше риск во-первых неполучения чистой прибыли, а во-вторых – банкротства предприятия. С другой стороны, финансовый леверидж способствует повышению рентабельности собственного капитала: не вкладывая в предприятие дополнительный собственный капитал (он замещается заемными средствами), владельцы получают большую сумму чистой прибыли, “заработанную” заемным капиталом. Кроме этого предприятие получает возможность воспользоваться “налоговым щитом”, так как в отличие от дивидендов по акциям сумма процентов за кредит вычитается из общей величины прибыли, подлежащей налогообложению. Однако, чтобы воспользоваться преимуществами финансового левериджа, предприятию необходимо выполнить обязательное условие – заработать операционную прибыль, достаточную как минимум для покрытия процентных платежей по заемным средствам. Являясь постоянной величиной по отношению к операционной прибыли, сумма процентов выполняет примерно ту же функцию, что и сумма фиксированных расходов в случае операционного левериджа: в точке ее покрытия возникает чистая прибыль и, чем выше плата за кредит, тем быстрее растет чистая прибыль на 1 акцию в окрестностях точки покрытия. По мере снижения операционной прибыли, величина чистого дохода каждого акционера также будет уменьшаться непропорционально быстро. Увеличение доли заемного капитала создает эффект рычага, действующего в обоих направлениях -– как в сторону повышения чистой прибыли на 1 акцию, так и в сторону ее снижения. Понуждая руководство предприятия увеличивать его финансовую зависимость от кредиторов, собственники полностью принимают на себя дополнительный финансовый риск: проценты по кредиту должны быть уплачены независимо от результатов работы, а выплата дивидендов производится только из чистой прибыли, которую предприятие может и не получить. Кроме того, в случае банкротства предприятия, кредиторы будут иметь преимущества в сравнении с акционерами на получение своей доли в его имуществе. Владельцы окажутся последними в очереди претендентов на остаточную стоимость ликвидируемого предприятия. Столь значительное повышение риска акционеров компенсируется более высоким уровнем рентабельности собственного капитала, который обеспечит предприятие в случае благополучного исхода. Таблица 5.7.1 Изменение чистой прибыли до уплаты налога на 1 акцию по отношению к операционной прибыли
Нанеся эти значения на график (рис. 5.7.1), можно видеть, что чистая прибыль на 1 акцию второго предприятия растет быстрее, чем первого, относительно операционной прибыли. То есть в случае роста операционной прибыли на 1 процентный пункт, чистая прибыль на 1 акцию у второго предприятия увеличится значительно быстрее. Точно так же она будет быстрее снижаться при уменьшении операционной прибыли на 1 пункт. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
