Курс лекций Метрология, стандартизация и сертификация. Курс лекций по дисциплине оп 05 Метрология, стандартизация и сертификация
 Скачать 215.26 Kb. Скачать 215.26 Kb.
|
|
Достоверность измерений – это характеристика, определяющая степень доверия к полученным результатам измерений. По данной характеристике измерения делятся на достоверные и недостоверные. Достоверность измерений зависит того, известна ли вероятность отклонения результатов измерения от настоящего значения измеряемой величины. Если же достоверность измерений не определена, то результаты таких измерений, как правило, не используются. Достоверность измерений ограничена сверху погрешностью измерений. 6. Понятие о физической величине. Значение систем физических единиц Физическая величина является понятием как минимум двух наук: физики и метрологии. По определению физическая величина представляет собой некое свойство объекта, процесса, общее для целого ряда объектов по качественным параметрам, отличающееся, однако, в количественном отношении (индивидуальная для каждого объекта). Классическим примером иллюстрации этого определения служит тот факт, что, обладая собственной массой и температурой, все тела имеют индивидуальные числовые значения этих параметров. Соответственно размер физической величины считается ее количественным наполнением, содержанием, а в свою очередь значение физической величины представляет собой числовую оценку ее размеров. В связи с этим существует понятие однородной физической величины, когда она является носителем аналогичного свойства в качественном смысле Таким образом, получение информации о значениях физической величины как некоего числа принятых для нее единиц и есть главная задача измерений. И, соответственно, физическая величина, которой по определению присвоено условное значение, равное единице, есть единица физической величины. Вообще же все значения физических величин традиционно делят на: истинные и действительные. Первые представляет собой значения, идеальным образом отражающие в качественном и количественном отношении соответствующие свойства объекта, а вторые – значения, найденные экспериментальным путем и настолько приближенные к истине, что могут быть приняты вместо нее. Однако этим классификация физических величин не исчерпывается. Есть целый ряд классификаций, созданных по различным признакам Основными из них является деления на: 1) активные и пассивные физические величины – при делении по отношению к сигналам измерительной информации. Причем первые (активные) в данном случае представляют собой величины, которые без использования вспомогательных источников энергии имеют вероятность быть преобразованными в сигнал измерительной информации. А вторые (пассивные) представляют собой такие величины, для измерения которых нужно использовать вспомогательные источники энергии, создающие сигнал измерительной информации; 2) аддитивные (или экстенсивные) и неаддитивные (или интенсивные) физические величины – при делении по признаку аддитивности. Считается, что первые (аддитивные) величины измеряются по частям, кроме того, их можно точно воспроизводить с помощью многозначной меры, основанной на суммировании размеров отдельных мер. А вторые (неаддитивные) величины прямо не измеряются, так как они преобразуются в непосредственное измерение величины или измерение путем косвенных измерений. В 1791 г. Национальным собранием Франции была принята первая в истории система единиц физических величин. Она представляла собой метрическую систему мер. В нее входили: единицы длин, площадей, объемов, вместимостей и веса. А в их основу были положены две общеизвестные ныне единицы: метр и килограмм. Ряд исследователей считают, что, строго говоря, эта первая система не является системой единиц в современном понимании. И лишь в 1832 г. немецким математиком К. Гауссом была разработана и опубликована новейшая методика построения системы единиц, представляющая собой в данном контексте некую совокупность основных и производных единиц. В основу своей методики ученый заложил три основные независимые друг от друга величины: массу, длину, время. А в качестве основных единиц измерения данных величин математик взял миллиграмм, миллиметр и секунду, поскольку все остальные единицы измерения можно с легкостью вычислить с помощью минимальных. К. Гаусс считал свою систему единиц абсолютной системой. С развитием цивилизации и научно—технического прогресса возникли еще ряд систем единиц физических величин, основанием для которых служит принцип системы Гаусса. Все эти системы построены как метрические, однако их отличием служат различные основные единицы. Так, на современном этапе развития выделяют следующие основные системы единиц физических величин: 1) система СГС (1881 г.) или Система единиц физических величин СГС, основными единицами которых являются следующие: сантиметр (см) – представленный в виде единицы длины, грамм (г) – в виде единицы массы, а также секунда (с) – в виде единицы времени; 2) система МКГСС (конец XIX в.), использующая первоначально килограмм как единицу веса, а впоследствии как единицу силы, что вызвало создание системы единиц физических величин, основными единицами которой стали три физических единицы: метр как единица длины, килограмм—сила как единица силы и секунда как единица времени; 3) система МКСА (1901 г.), основы которой были созданы итальянским ученым Дж. Джорджи, который предложил в качестве единиц системы МКСА метр, килограмм, секунду и ампер. На сегодняшний день в мировой науке существует неисчислимое количество всевозможных систем единиц физических величин, а также немало так называемых внесистемных единиц. Это, конечно, приводит к определенным неудобствам при вычислениях, вынуждая прибегать к пересчету при переводе физических величин из одной системы единиц в другую. Сложилась ситуация, при которой возникла серьезная необходимость унификации единиц измерения. Требовалось создать такую систему единиц физических величин, которая подходила бы для большинства различных отраслей области измерений. Причем в роли главного акцента должен был звучать принцип когерентности, подразумевающий под собой, что единица коэффициента пропорциональности равна в уравнениях связи между физическими величинами. Подобный проект был создан в 1954 г. комиссией по разработке единой Международной системы единиц. Он носил название «проект Международной системы единиц» и был в конце концов утвержден Генеральной конференцией по мерам и весам. Таким образом, система, основанная на семи основных единицах, стала называться Международной системой единиц, или сокращенно СИ, что происходит от аббревиатуры французского наименования «Systeme International* (SI). Международная система единиц, или сокращенно СИ, содержит семь основных, две дополнительных, а также несколько внесистемных, логарифмических единиц измерения, что можно видеть в таблице 1. Таблица 1 Международная система единиц или СИ 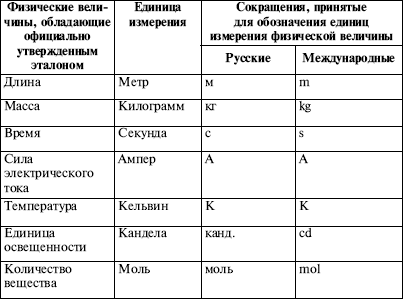 Решениями Генеральной конференции по мерам и весам приняты такие определения основных единиц измерения физических величин: 1) метр считается длинной пути, который проходит свет в вакууме за 1/299 792 458 долю секунды; 2) килограмм считается приравненным к существующему международному прототипу килограмма; 3) секунда равна 919 2631 770 периодам излучения, соответствующего тому переходу, который происходит между двумя так называемыми сверхтонкими уровнями основного состояния атома Cs133; 4) ампер считается мерой той силы неизменяющегося тока, вызывающего на каждом участке проводника длиной 1 м силу взаимодействия при условии прохождения по двум прямолинейным параллельным проводникам, обладающим такими показателями, как ничтожно малая площадь кругового сечения и бесконечная длина, а также расположение на расстоянии в 1 м друг от друга в условиях вакуума; 5) кельвин равен 1/273,16 части термодинамической температуры, так называемой тройной точки воды; 6) моль равен количеству вещества системы, в которую входит такое же количество структурных элементов, что и в атомы в C 12 массой 0,012 кг. Кроме того, Международная система единиц содержит две достаточно важные дополнительные единицы, необходимые для измерения плоского и телесного углов. Так, единица плоского угла – это радиан, или сокращенно рад, представляющий собой угол между двух радиусов окружности, длина дуги между которыми равняется радиусу окружности. Если речь идет о градусах, то радиан равен 57°17 48 '. А стерадиан, или ср, принимаемый за единицу телесного угла, представляет собой, соответственно, телесный угол, расположение вершины которого фиксируется в центре сферы, а площадь, вырезаемая данным углом на поверхности сферы, равна площади квадрата, сторона которого равна длине радиуса сферы Другие дополнительные единицы СИ используются для формирования единиц угловой скорости, а также углового ускорения и т. д. Радиан и стерадиан используются для теоретических построений и расчетов, поскольку большая часть значимых для практики значений углов в радианах выражаются трансцендентными числами. К внесистемным единицам относятся следующие: 1) за логарифмическую единицу принята десятая часть бела, децибел (дБ); 2) диоптрия – сила света для оптических приборов; 3) реактивная мощность – Вар (ВА); 4) астрономическая единица (а. е.) – 149,6 млн км; 5) световой год, под которым понимается такое расстояние, которое луч света проходит за 1 год; 6) вместимость – литр; 7) площадь – гектар (га). Кроме того, логарифмические единицы традиционно делят на абсолютные и относительные. Первые абсолютные логарифмические единицы – это десятичный логарифм соотношения физической величины и нормированного значения Относительная логарифмическая единица образуется как десятичный логарифм отношения любых двух однородных величин. Существуют также единицы, вообще не входящие в СИ. Это в первую очередь такие единицы, как градус и минута. Все остальные единицы считаются производными, которые согласно Международной системе единиц образуются с помощью самых простейших уравнений с использованием величин, числовые коэффициенты которых приравнены к единице. Если в уравнении числовой коэффициент равен единице, производная единица называется когерентной. 7. Физические величины и измерения Объектом измерения для метрологии, как правило, являются физические величины. Физические величины используется для характеристики различных объектов, явлений и процессов. Разделяют основные и производные от основных величины. Семь основных и две дополнительных физических величины установлены в Международной системе единиц. Это длина, масса, время, термодинамическая температура, количество вещества, сила света и сила электрического тока, дополнительные единицы – это радиан и стерадиан. У физических величин есть качественные и количественные характеристики. Качественное различие физических величин отражается в их размерности. Обозначение размерности установлено международным стандартом ИСО, им является символ dim*. Таким образом, размерность длины, массы и времени: dim*l = L, dim*m = M, dim*t = T. Для производной величины размерность выражается посредством размерности основных величин и степенного одночлена: dim*Y = L k × M 1 × T m, где k, I, m– показатели степени размерности основных величин. Показатель степени размерности может принимать различные значения и разные знаки, может быть как целым, так и дробным, может принимать значение ноль. Если при определении размерности производной величины все показатели степени размерности равны нулю, то основание степени, соответственно, принимает значение единицы, таким образом, величина является безразмерной. Размерность производной величины может также определяться как отношение одноименных величин, тогда величина является относительной. Размерность относительной величины может также быть логарифмической. Количественная характеристика объекта измерения – это его размер, полученный в результате измерения. Самый элементарный способ получить сведения о размере определенной величины объекта измерения – это сравнить его с другим объектом. Результатом такого сравнения не будет точная количественная характеристика, оно позволит лишь выяснить, какой из объектов больше (меньше) по размеру. Сравниваться могут не только два, но и большее число размеров. Если размеры объектов измерения расположить по возрастанию или по убыванию, то получится шкала порядка. Процесс сортировки и расположения размеров по возрастанию или по убыванию по шкале порядка называетсяранжированием. Для удобства измерений определенные точки на шкале порядка фиксируются и называются опорными, или реперными точками Фиксированным точкам шкалы порядка могут ставиться в соответствие цифры, которые часто называют баллами. У реперных шкал порядка есть существенный недостаток: неопределенная величина интервалов между фиксированными реперными точками. В этом плане преимущество есть у шкалы интервалов Шкалой интервалов является, например, шкала измерения времени. Она поделена на большие интервалы – годы, большие интервалы поделены на меньшие – сутки. С помощью шкалы интервалов можно определить не только, какой из размеров больше, но и насколько один размер больше другого. Недостаток шкалы интервалов заключается в том, что с ее помощью нельзя определить, во сколько раз данный размер больше другого, потому что на шкале интервалов зафиксирован только масштаб, а начало отсчета не фиксировано и может устанавливаться произвольно. Самым оптимальным вариантом является шкала отношений. Шкалой отношений является, например, шкала температуры Кельвина. На данной шкале есть фиксированное начало отсчета – абсолютный ноль (температура, при которой прекращается тепловое движение молекул). Основное преимущество шкалы отношений состоит в том, что с ее помощью можно определить, во сколько раз один размер больше или меньше другого. Размер объекта измерения может быть представлен в разных видах. Это зависит от того, на какие интервалы разбита шкала, с помощью которой измеряется данный размер. Например, время движения может быть представлено в следующих видах: T = 1 ч = 60 мин = 3600 с. Это значения измеряемой величины. 1, 60, 3600 – это числовые значения данной величины. Значение величины может быть вычислено с помощью основного уравнения измерения, которое имеет вид: Q = X [Q], где Q – значение величины; X – числовое значение данной величины в установленной для нее единице; [Q] – установленная для данного измерения единица. 8. Эталоны и образцовые средства измерений Все вопросы, связанные с хранением, применением и созданием эталонов, а также контроль за их состоянием, решаются по единым правилам, установленным ГОСТом «ГСИ. Эталоны единиц физических величин. Основные положения» и ГОСТом «ГСИ. Эталоны единиц физических величин. Порядок разработки и утверждения, регистрации, хранения и применения». Классифицируются эталоны по принципу подчиненности. По этому параметру эталоны бывают первичные и вторичные. Первичный эталон должен служить целям обеспечения воспроизведения, хранения единицы и передачи размеров с максимальной точностью, которую можно получить в данной сфере измерений. В свою очередь, первичные могут быть специальными первичными эталонами, которые предназначены для воспроизведения единицы в условиях, когда непосредственная передача размера единицы с необходимой достоверностью практически не может быть осуществлена например для малых и больших напряжений, СВЧ и ВЧ. Их утверждают в виде государственных эталонов. Поскольку налицо особая значимость государственных эталонов, на любой государственный эталон утверждается ГОСТом. Другой задачей этого утверждения становится придание данным эталонам силы закона. На Государственный комитет по стандартам возложена обязанность создавать, утверждать, хранить и применять государственные эталоны. Вторичный эталон воспроизводит единицу при особенных условиях, заменяя при этих условиях первичный эталон. Он создается и утверждается для целей обеспечения минимального износа государственного эталона. Вторичные эталоны могут делиться по признаку назначения. Так, выделяют: 1) эталоны—копии, предназначенные для передачи размеров единиц рабочим эталонам; 2) эталоны—сравнения, предназначенных для проверки невредимости государственного эталона, а также для целей его заменяя при условии его порчи или утраты; 3) эталоны—свидетели, предназначенные для сличения эталонов, которые по ряду различных причин не подлежат непосредственному сличению друг с другом; 4) рабочие эталоны, которые воспроизводят единицу от вторичных эталонов и служат для передачи размера эталону более низкого разряда. Вторичные эталоны создают, утверждают, хранят и применяют министерства и ведомства. Существует также понятие «эталон единицы», под которым подразумевают одно средство или комплекс средств измерений, направленных на воспроизведение и хранение единицы для последующей трансляции ее размера нижестоящим средствам измерений, выполненных по особой спецификации и официально утвержденных в установленном порядке в качестве эталона. Есть два способа воспроизведения единиц по признаку зависимости от технико—экономических требований: 1) централизованный способ – с помощью единого для целой страны или же группы стран государственного эталона. Централизованно воспроизводятся все основные единицы и большая часть производных; 2) децентрализованный способ воспроизведения – применим к производным единицам, сведения о размере которых не передаются непосредственным сравнением с эталоном. Трансляция размера может происходить разными методами поверки. Как правило, передача размера осуществляется известными методами измерений. С одной стороны, существует определенный недостаток передачи размера ступенчатым способом, который подразумевает, что порой происходит потеря точности. С другой стороны, есть здесь и свои положительные моменты, которые подразумевают, что данная многоступенчатость помогает оберегать эталоны и передавать размер единицы всем рабочим средствам измерения. Существует также понятие «образцовые средства измерений», которые используются для закономерной трансляции размеров единиц в процессе поверки средств измерения и используются лишь в подразделениях метрологической службы. Разряд образцового средства измерения определяется в ходе измерений метрологической аттестации одним из органов Государственного комитета по стандартам. При необходимости особо точные рабочие средства измерения в вышеуказанном порядке могут быть аттестованы на обусловленный период как образцовые средства измерения. И наоборот, образцовые средства измерения, не прошедшие очередную аттестацию по разным причинам, используются как рабочие средства измерения.[1] 9. Средства измерений и их характеристики В научной литературе средства технических измерений делят на три большие группы. Это: меры, калибры и универсальные средства измерения, к которым относятся измерительные приборы, контрольно—измерительные приборы (КИП), и системы. 1. Мера представляет собой такое средство измерений, которое предназначается для воспроизведения физической величины положенного размера. К мерам относятся плоскопараллельные меры длины (плитка) и угловые меры. 2. Калибры представляют собой некие устройства, предназначение которых заключается в использовании для контролирования и поиска в нужных границах размеров, взаиморасположения поверхностей и формы деталей. Как правило, они подразделяются на: гладкие предельные калибры (скобы и пробки), а также резьбовые калибры, к которым относятся резьбовые кольца или скобы, резьбовые пробки и т. п. 3. Измерительный прибор, представленный в виде устройства, вырабатывающего сигнал измерительной информации в форме, понятной для восприятия наблюдателей. 4. Измерительная система, понимаемая как некая совокупность средств измерений и неких вспомогательных устройств, которые соединяются между собой каналами связи. Она предназначена для производства сигналов информации измерений в некой форме, которая подходит для автоматической обработки, а также для трансляции и применения в автоматических системах управления. 5. Универсальные средства измерения, предназначение которых находится в использовании для определения действительных размеров. Любое универсальное измерительное средство характеризуется назначением, принципом действия, т. е физическим принципом, положенным в основу его построения, особенностями конструкции и метрологическими характеристиками. При контрольном измерении угловых и линейных показателей применяют прямые измерения, реже встречаются относительные, косвенные или совокупные измерения. В научной литературе среди прямых методов измерений выделяют, как правило, следующие: 1) метод непосредственной оценки, представляющий собой такой метод, при котором значение величины определяют по отсчетному устройству измерительного прибора; 2) метод сравнения с мерой, под которым понимается метод, при котором данную величину возможно сравнить с величиной, воспроизводимой мерой; 3) метод дополнения, под которым обычно подразумевается метод, когда значение полученной величины дополняется мерой этой же величины с тем, чтобы на используемый прибор для сравнения действовала их сумма, равная заранее заданному значению; 4) дифференциальный метод, который характеризуется измерением разности между данной величиной и известной величиной, воспроизводимой мерой. Метод дает результат с достаточно высоким показателем точности при применении грубых средств измерения; 5) нулевой метод, который, по сути, аналогичен дифференциальному, но разность между данной величиной и мерой сводится к нулю. Причем нулевой метод обладает определенным преимуществом, поскольку мера может быть во много раз меньше измеряемой величины; 6) метод замещения, представляющий собой сравнительный метод с мерой, в которой измеряемую величину заменяют известной величиной, которая воспроизводится мерой. Вспомним о том, что существуют и нестандартизованные методы. В эту группу, как правило, включают следующие: 1) метод противопоставления, подразумевающий под собой такой метод, при котором данная величина, а также величина, воспроизводимая мерой, в одно и то же время действуют на прибор сравнения; 2) метод совпадений, характеризующийся как метод, при котором разность между сравниваемыми величинами измеряют, используя совпадение меток на шкалах или периодических сигналов. 10. Классификация средств измерения |
