Курс лекций Метрология, стандартизация и сертификация. Курс лекций по дисциплине оп 05 Метрология, стандартизация и сертификация
 Скачать 215.26 Kb. Скачать 215.26 Kb.
|
|
Простой измерительный канал – это канал, в котором используется прямой метод измерений, реализующийся посредством упорядоченных измерительных преобразований. В сложном измерительном канале выделяют первичную часть и вторичную часть. В первичной части сложный измерительный канал является объединением некоторого числа простых измерительных каналов. Сигналы с выхода простых измерительных каналов первичной части применяются для косвенных, совокупных или совместных измерений или для получения пропорционального результату измерений сигнала во вторичной части. Измерительный компонент измерительной системы – это средство измерений, обладающее отдельно нормированными метрологическими характеристиками. Примером измерительного компонента измерительной системы может послужить измерительный прибор. К измерительным компонентам измерительной системы принадлежат также аналоговые вычислительные устройства (устройства, выполняющие измерительные преобразования). Аналоговые вычислительные устройства принадлежат к группе устройств с одним или несколькими вводами. Измерительные компоненты измерительных систем бывают следующих видов. Связующий компонент – это технический прибор или элемент окружающей среды, применяющиеся в целях обмена сигналами, содержащими сведения об измеряемой величине, между компонентами измерительной системы с минимально возможными искажениями. Примером связующего компонента может послужить телефонная линия, высоковольтная линия электропередачи, переходные устройства. Вычислительный компонент – это цифровое устройство (часть цифрового устройства), предназначенное для выполнения вычислений, с установленным программным обеспечением. Вычислительный компонент применяется для вычи сления результатов измерений (прямых, косвенных, совместных, совокупных), которые представляют собой число или соответствующий код, вычисления производятся по итогам первичных преобразований в измерительной системе. Вычислительный компонент выполняет также логические операции и координирование работы измерительной системы. Комплексный компонент – это составная часть измерительной системы, представляющая собой технически или территориально объединенную совокупность компонентов Комплексный компонент завершает измерительные преобразования, а также вычислительные и логические операции, которые утверждены в принятом алгоритме обработки результатов измерений для других целей. Вспомогательный компонент – это технический прибор, предназначенный для обеспечения нормального функционирования измерительной системы, но не принимающий участия в процессе измерительных преобразований. Согласно соответствующим ГОСТам метрологические характеристики измерительной системы должны быть в обязательном порядке нормированы для каждого измерительного канала, входящего в измерительную систему, а также для комплексных и измерительных компонентов измерительной системы. Как правило, изготовитель измерительной системы определяет общие нормы на метрологические характеристики измерительных каналов измерительной системы. Нормированные метрологические характеристики измерительных каналов измерительной системы призваны: 1) обеспечивать определение погрешности измерений с помощью измерительных каналов в рабочих условиях; 2) обеспечивать эффективный контроль над соответствием измерительного канала измерительной системы нормированным метрологическим характеристикам в процессе испытаний измерительной системы. В случае, если определение или контроль над метрологическими характеристиками измерительного канала измерительной системы не могут осуществляться экспериментальным путем для всего измерительного канала, нормирование метрологических характеристик проводится для составных частей измерительного канала. Причем, объединение этих частей должно представлять собой целый измерительный канал Нормировать характеристики погрешности в качестве метрологических характеристик измерительного канала измерительной системы можно как при нормальных условиях использования измерительных компонентов, так и при рабочих условиях, для которых характерно такое сочетание влияющих факторов, при котором модуль численного значения характеристик погрешности измерительного канала имеет максимально возможное значение. Для большей эффективности для промежуточных сочетаний влияющих факторов также нормируются характеристики погрешностей измерительного канала. Данные характеристики погрешности измерительных каналов измерительной системы необходимо проверять посредством их расчета по метрологическим характеристикам компонентов измерительной системы, представляющих собой в целом измерительный канал. Причем рассчитанные значения характеристик погрешности измерительных каналов могут и не проверяться экспериментальным путем. Но тем не менее в обязательном порядке должен осуществляться контроль метрологических характеристик для всех составных частей (компонентов) измерительной системы, нормы которых являются исходными данными в расчете. Нормированные метрологические характеристики комплексных компонентов и измерительных компонентов должны: 1) обеспечивать определение характеристик погрешности измерительных каналов измерительной системы при рабочих условиях применения с использованием нормированных метрологических характеристик компонентов; 2) обеспечивать осуществление эффективного контроля над данными компонентами в процессе испытаний, проводимых с целью установления типа, и поверке соответствия нормированным метрологическим характеристикам. Для вычислительных компонентов измерительной системы, в случае, если их программное обеспечение не учитывалось в процессе нормирования метрологических характеристик, нормируются погрешности вычислений, источником которых является функционирование программного обеспечения (алгоритм вычислений, его программная реализация). Для вычислительных компонентов измерительной системы могут также нормироваться другие характеристики, при условии учета специфики вычислительного компонента, которая может воздействовать на характеристики составляющих частей погрешности измерительного канала (характеристики составляющей погрешности), если составляющая погрешность возникает из—за использования данной программы обработки результатов измерений. Техническая документация по эксплуатации измерительной системы должна включать в себя описание алгоритма и программы, работающей в соответствии с описанным алгоритмом. Данное описание должно позволять рассчитывать характеристики погрешности результатов измерений с использованием характеристик погрешности составной части измерительного канала измерительной системы, расположенной перед вычислительным компонентом. Для связующих компонентов измерительной системы нормируются два вида характеристик: 1) характеристики, обеспечивающие такое значение составляющей погрешности измерительного канала, вызванной связующим компонентом, которым можно пренебречь; 2) характеристики, позволяющие определить значение составляющей погрешности измерительного канала, вызванной связующим компонентом. 18. Выбор средств измерений При выборе средств измерений в первую очередь должно учитываться допустимое значение погрешности для данного измерения, установленное в соответствующих нормативных документах. В случае, если допустимая погрешность не предусмотрена в соответствующих нормативных документах, предельно допустимая погрешность измерения должна быть регламентирована в технической документации на изделие. При выборе средств измерения должны также учитываться: 1) допустимые отклонения; 2) методы проведения измерений и способы контроля. Главным критерием выбора средств измерений является соответствие средств измерения требованиям достоверности измерений, получения настоящих (действительных) значений измеряемых величин с заданной точностью при минимальных временных и материальных затратах. Для оптимального выбора средств измерений необходимо обладать следующими исходными данными: 1) номинальным значением измеряемой величины; 2) величиной разности между максимальным и минимальным значением измеряемой величины, регламентируемой в нормативной документации; 3) сведениями об условиях проведения измерений. Если необходимо выбрать измерительную систему, руководствуясь критерием точности, то ее погрешность должна вычисляться как сумма погрешностей всех элементов системы (мер, измерительных приборов, измерительных преобразователей), в соответствии с установленным для каждой системы законом. Предварительный выбор средств измерений производится в соответствии с критерием точности, а при окончательном выборе средств измерений должны учитываться следующие требования: 1) к рабочей области значений величин, оказывающих влияние на процесс измерения; 2) к габаритам средства измерений; 3) к массе средства измерений; 4) к конструкции средства измерений. При выборе средств измерений необходимо учитывать предпочтительность стандартизированных средств измерений. 19. Методы определения и учета погрешностей Методы определения и учета погрешностей измерений используются для того, чтобы: 1) на основании результатов измерений получить настоящее (действительное) значение измеряемой величины; 2) определить точность полученных результатов, т. е. степень их соответствия настоящему (действительному) значению. В процессе определения и учета погрешностей оцениваются: 1) математическое ожидание; 2) среднеквадратическое отклонение. Точечная оценка параметра (математического ожидания или среднеквадратического отклонения) – это оценка параметра, которая может быть выражена одним числом. Точечная оценка является функцией от экспериментальных данных и, следовательно, сама должна быть случайной величиной, распределенной по закону, зависящему от закона распределения для значений исходной случайной величины Закон распределения значений точечной оценки будет зависеть также от оцениваемого параметра и от числа испытаний (экспериментов). Точечная оценка бывает следующих видов: 1) несмещенная точечная оценка; 2) эффективная точечная оценка; 3) состоятельная точечная оценка. Несмещенная точечная оценка – это оценка параметра погрешности, математическое ожидание которой равно этому параметру. Эффективная точечная оценка – это точечная оценка. дисперсия которой меньше, чем дисперсия другой какой угодно оценки этого параметра. Состоятельная точечная оценка – это оценка, которая при увеличении числа испытаний стремится к значению параметра, подвергающегося оценке. Основные методы определения оценок: 1) метод максимального правдоподобия (метод Фишера); 2) метод наименьших квадратов. 1. Метод максимального правдоподобия основывается на идее, что сведения о действительном значении измеряемой величины и рассеивании результатов измерений, полученные путем многократных наблюдений, содержатся в ряде наблюдений. Метод максимального правдоподобия состоит в поиске оценок, при которых функция правдоподобия проходит через свой максимум. Оценки максимального правдоподобия – это оценки сред—неквадратического отклонения и оценки истинного значения. Если случайные погрешности распределены по нормальному закону распределения, то оценка максимального правдоподобия для истинного значения представляет собой среднее арифметическое результатов наблюдений, а оценка дисперсии является средним арифметическим квадратов отклонений значений от математического ожидания. Преимущества оценок максимального правдоподобия заключается в том, что данные оценки: 1) несмещенные асимптотически; 2) асимптотически эффективные; 3) асимптотически распределены по нормальному закону. 2. Метод наименьших квадратов состоит в том, что из определенного класса оценок берут ту оценку, у которой минимальная дисперсия (самую эффективную). Из всех линейных оценок действительного значения, где присутствуют некоторые постоянные, только среднее арифметическое сводит к наименьшему значению дисперсии. В связи с этим при условии распределения значений случайных погрешностей по нормальному закону распределения оценки, полученные с использованием метода наименьших квадратов, идентичны оценкам максимального правдоподобия. Оценка параметров с помощью интервалов проводится посредством нахождения доверительных интервалов, в пределах которых с заданными вероятностями располагаются действительные значения оцениваемых параметров. Доверительная граница случайного отклонения – это число, представляющее собой длину доверительного интервала, разделенную пополам. При достаточно большом количестве испытаний доверительный интервал существенно уменьшается. Если увеличивается число испытаний, то допустимо увеличить число доверительных интервалов. Обнаружение грубых погрешностей Грубые погрешности – это погрешности, намного превышающие предполагаемые в данных условиях проведения измерений систематические и случайные погрешности. Промахи и грубые погрешности могут появляться из—за грубых ошибок в процессе проведения измерения, технической неисправности средства измерения, неожиданного изменения внешних условий. Для того чтобы исключить грубые погрешности, рекомендуется до начала измерений приближенно определить значение измеряемой величины. В случае, если при проведении измерений выясняется, что результат отдельного наблюдения сильно отличается от других полученных результатов, нужно обязательно установить причины такого отличия. Результаты, полученные с резким отличием, можно отбросить и повторно измерить данную величину. Однако в некоторых случаях отбрасывание таких результатов может вызвать ощутимое искажение рассеивания ряда измерений. В связи с этим рекомендуется не отбрасывать необдуманно отличающиеся результаты, а дополнять их результатами повторных измерений. Если необходимо исключить грубые погрешности в процессе обработки полученных результатов, когда уже нельзя скорректировать условия проведения измерений и провести повторные измерения, то применяются статистические методы. Общий метод проверки статистических гипотез позволяет выяснить, присутствует ли в данном результате измерений грубая погрешность. 20. Обработка и представление результатов измерения Обычно измерения являются однократными. При обычных условиях их точности вполне достаточно. Результат однократного измерения представляется в следующем виде: Qi = Yi + Ωi, где Yi – значение i – го показания; Ωi – поправка. Погрешность результата однократного измерения определяется при утверждении метода проведения измерений. В процессе обработки результатов измерений используются различные виды закона распределения (нормальный закон распределения, равномерный закон распределения корреляционный закон распределения) измеряемой величины (в данном случае она рассматривается как случайная). Обработка результатов прямых равноточных измерений Прямые измерения – это измерения, посредством которых непосредственно получается значение измеряемой величины Равноточными или равнорассеянными называют прямые, взаимно независимые измерения определенной величины, причем результаты этих измерений могут быть рассмотрены как случайные и распределенные по одному закону распределения. Обычно при обработке результатов прямых равноточных измерений предполагается, что результаты и погрешности измерений распределены по нормальному закону распределения. После снятия расчетов вычисляется значение математического ожидания по формуле: 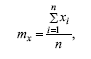 где xi – значение измеряемой величины; n – количество проведенных измерений. Затем, если систематическая погрешность определена, ее значение вычитают из вычисленного значения математического ожидания. Потом вычисляется значение среднеквадратического отклонения значений измеряемой величины от математического ожидания. Алгоритм обработки результатов многократных равноточных измерений Если известна систематическая погрешность, то ее необходимо исключить из результатов измерений. Вычислить математическое ожидание результатов измерений. В качестве математического ожидания обычно берется среднее арифметическое значений. Установить величину случайной погрешности (отклонения от среднего арифметического) результата однократного измерения. Вычислить дисперсию случайной погрешности. Вычислить среднеквадратическое отклонение результата измерения. Проверить предположение, что результаты измерений распределены по нормальному закону. Найти значение доверительного интервала и доверительной погрешности. Определить значение энтропийной погрешности и энтропийного коэффициента. 21. Поверка и калибровка средств измерений Калибровка средств измерений – это комплекс действий и операций, определяющих и подтверждающих настоящие (действительные) значения метрологических характеристик и (или) пригодность средств измерений, не подвергающихся государственному метрологическому контролю. Пригодность средства измерений – это характеристика, определяющаяся соответствием метрологических характеристик средства измерения утвержденным (в нормативных документах, либо заказчиком) техническим требованиям Калибровочная лаборатория определяет пригодность средства измерений. Калибровка сменила поверку и метрологическую аттестацию средств измерений, которые проводились только органами государственной метрологической службы. Калибровка, в отличие от поверки и метрологической аттестации средств измерений, может осуществляться любой метрологической службой при условии, что у нее есть возможность обеспечить соответствующие условия для проведения калибровки. Калибровка осуществляется на добровольной основе и может быть проведена даже метрологической службой предприятия. Но тем не менее метрологическая служба предприятия обязана выполнять определенные требования. Основное требование к метрологической службе – обеспечение соответствия рабочего средства измерений государственному эталону, т. е. калибровка входит в состав национальной системы обеспечения единства измерений. Выделяют четыре метода поверки (калибровки) средств измерений: 1) метод непосредственного сравнения с эталоном; 2) метод сличения при помощи компьютера; 3) метод прямых измерений величины; 4) метод косвенных измерений величины. |
