Курс лекций по электротехнике Барнаул, 2000

• Название: Курс лекций по электротехнике Барнаул, 2000
• Дата: 18.11.2022
• Размер: 1.86 Mb.
• Имя файла: e9247be.doc
• Тип: Курс лекций; #795504
• страница: 3 из 5

РАЗДЕЛ 3. ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
3.1. ЭЛЕМЕНТЫ ТРЕХФАЗНОЙ СИСТЕМЫ
В настоящее время получение, передача и распределение электроэнергии в большинстве случаев производится посредством трехфазной системы.

Эта система была изобретена и практически разработала во всех основных се частях выдающимся русским инженером М. О. Доливо-Добровольским.

Как показывает само название, трехфазная система состоит из трех источников электроэнергии и трех цепей, соединенных общими проводами линии передачи.

Источником энергии для всех фаз системы является трехфазный генератор (рис. 3.1). Он отличается от однофазного генератора переменного тока тем, что у него на статоре размещены три изолированные друг от друга одинаковые обмотки. Они расположены так, чтобы индуктируемые в них э.д.с. были сдвинуты по фазе одна относительно другой на 120°.

Если генератор двухполюсный, как на рис. 3.1, то оси катушек обмоток фазы сдвинуты одна по отношению к другой на одну треть окружности статора.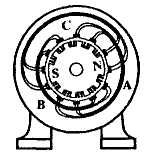



Рис.3.1 Схема устройства трехфазного генератора.


При вращении ротора его постоянное магнитное поле пересекает проводники обмоток не одновременно. Э.д.с. обмотки А достигает своего максимального значения, когда мимо нее проходит середина полюса ротора. Э.д.с. в следующей обмотке В достигает максимума позже, когда ротор повернется на 1/3 оборота. В двухполюсном генераторе повороту на 1/3 оборота соответствует 1/3 периода индуктируемой э.д.с. Следовательно, э.д.с. в обмотке В отстает по фазе от э.д.с. в обмотке А на 1/3 периода. В свою очередь, э.д.с. в обмотке С отстает по фазе от э.д.с. обмотки Д на 1/3 периода и от э.д.с. обмотки А на 2/3 периода. При такой симметрии устройства генератора максимальные значения этих э.д.с. одинаковы. Конструкция генератора должна обеспечивать их синусоидальность.

Уравнения мгновенных значений э.д.с. будут: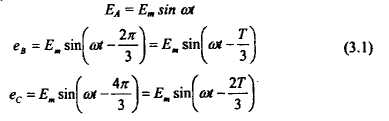



Кривые мгновенных значении э.д.с. показаны на рис. 3.2. На рис. 3.3 дана векторная диаграмма для их действующих значений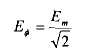



Сумма этих векторов образует замкнутый треугольник: Е_А+ ЕВ+ Ес = О — это трехфазная симметричная система э.д.с. Алгебраическая сумма мгновенных значений э.д.с. еA+ еB+ еC = О, что легко проверить, подставив выражения этих значений как синусоидальных функций времени.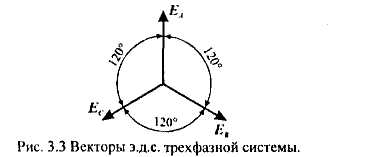



Изображения э.д.с. трехфазной системы в комплексной форме будут: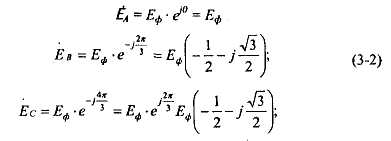



От последовательности фаз системы зависит направление вращения трехфазных двигателей, поэтому в трехфазных устройствах она проверяется специальными указателями последовательности фаз и обозначается раскраской шин на распределительных устройствах; приняты следующие цвета: фаза А — желтый, фаза В — зеленый и фаза С — красный; незаземленная нейтраль — белый, заземленная нейтраль — черный. Зажимы обмоток генератора различают: начала Л, В, С, концы X, Y, Z.

Два основных способа соединения обмоток генераторов, трансформаторов и приемников в трехфазных цепях: звездой и треугольником.

3.2. СОЕДИНЕНИЕ ФАЗ ЗВЕЗДОЙ
Обмотки фаз генераторов можно было бы соединить с тремя приемниками электроэнергии шестью проводами (рис. 3.4а) и получить таким путем три независимые фазные цепи. Практически подобное соединение применяется лишь в редких случаях, но с помощью такой схемы можно нагляднее представить условия, возникающие при объединении цепей в трехфазную систему. Как и в однофазных цепях переменного тока, стрелки на схеме показывают положительные направления фазных э.д.с. и создаваемых ими токов. Положительные направления определяет разметка зажимов обмоток фаз генератора. Внутри обмоток э.д.с. и токи направлены от «концов» (X, Y, Z) к «началам» (А, В, С). Во внешней цепи токи направлены от начал обмоток фаз генераторов к приемникам.

Для соединения звездой (условное обозначение Y) зажимы X, Y, Z («концы» обмоток фаз генератора) объединяются в одну общую точку N. Соответственно в точке и объединяются и три конца фазных цепей приемника (рис. 3.4 б) Между нейтральными точками генератора и приемника проложен общий нейтральный провод (или нейтраль) трехфазной системы, образуемый объединением трех обратных проводов.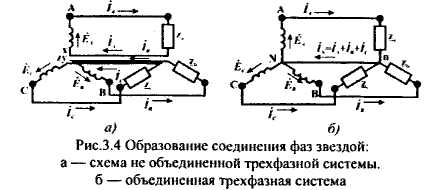



Если предположить равными нулю поочередно все фазные эдс, кроме одной (например, проследить в объединенной системе контур тока 1Л при наличии в системе одной э.д.с. Е_А) то легко убедиться, что объединение системы не изменит контуры, по которым замыкаются фазные токи. Следовательно, в нейтральном проводе системы ток будет равен векторной сумме фазных токов:



Нагрузка всех трех фаз называется симметричной, если ток во всех фазах одинаков и равны сдвиги фаз между фазными напряжениями и токами, а также полные сопротивления отдельных фаз приемника (т, е. равны комплексные сопротивления фаз приемника).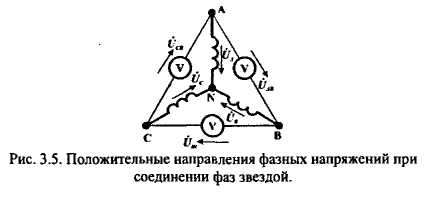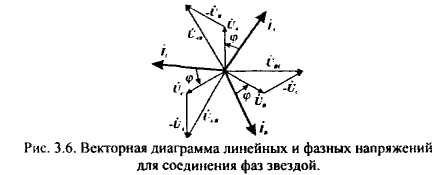





При симметричной нагрузке сумма векторов фазных токов образует замкнутый треугольник. Следовательно, в этом случае ток в нейтральном проводе I_N= 0. По этой причине для заведомо симметричной трехфазной нагрузки нейтральный провод не нужен. В частности, он не используется для трехфазных двигателей.

При соединении звездой фаз генератора и приемника напряжения на их зажимах называются фазными напряжениями U_ф (U_A , U_B, U_Cна рис. 3.5). Но в системе имеются также напряжения между линейными проводами, называемые линейными напряжениями Uл {U_AB,U_DC. U_CА) Положительные направления фазных напряжений противоположны по отношению к приемнику, включенному между линейными проводами (рис. 3.5). Следовательно, каждое из трех линейных напряжений равно векторной разности соответствующих фазных напряжений: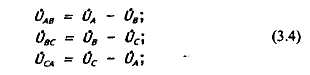



Численные соотношения между линейными и фазными напряжениями в симметричной системе легко определить на основании векторной диаграммы (рис. 3.6). За основу диаграммы можно взять три вектора фазных напряжений U_A, U_B и U_C. Углы между ними равны 120' . Для построения вектора линейного напряжения Uав следует из U_Aвычесть U_B, следовательно, нужно к U_Aприбавить (—U_B).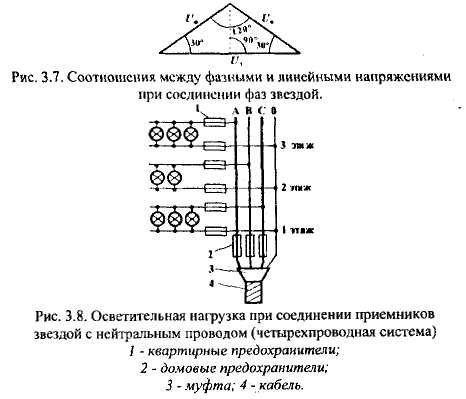



Последний равен U_Bпо величине, но противоположен ему по направлению. Так же строятся U_BCи U_CA.Так как рассматриваемая система напряжений симметрична, то векторы фазных и линейных напряжений образуют три равнобедренных треугольника с острыми углами по 30° и тупым углом 120°. Опустив из вершины тупого угла любого из треугольников перпендикуляр на противоположную сторону (рис. 3.7), можно найти, что



В трехфазной системе, соединенной звездой, линейные напряжения больше фазных в √3 раз. При смешанной осветительной и силовой нагрузке линейное напряжение 380 В подается на зажимы трехфазных двигателей, а фазное 220 В=380/√3 — на осветительные приборы.

При соединении звездой токи в проводах линии передачи— линейные токи Ijiравны фазным, так как все части фазной цепи и линейные провода соединены последовательно: Iл = Iф,

При осветительной нагрузке в случае соединения звездой приемники включаются между линейными проводами и нейтральным проводом,

Часто осветительная нагрузка бывает несимметричной, в этом случае необходим нейтральный провод (рис. 3.8). При отсутствии нейтрального провода в зависимости от отношения сопротивлений фаз приемника одно фазное напряжение может быть ниже необходимого, а другое слишком велико. По этой причине в нейтральном проводе магистрали запрещается устанавливать предохранители или выключатели.
3.3. СОЕДИНЕНИЕ ФАЗ ТРЕУГОЛЬНИКОМ
Несколько реже, чем соединение звездой, в трехфазных устройствах применяют соединение треугольником (условное обозначение Δ).

При соединении треугольником (рис. 3.9) обмотки фаз генератора соединяются так, чтобы начало одной обмотки фазы соединялось с концом предыдущей (А с Z; В с Xи С с Y). Положительные направляя э.д.с. при таком соединении направлены внутри треугольника обмоток фаз одинаково; следовательно, внутри этого треугольника действует алгебраическая сумма мгновенных значений фазных э.д.с. е_A + е_B + е_C= 0 и поэтому уравнительного тока в мотках генератора не возникает⁶. Общие точки, созданные объединением двух зажимов обмоток, соединяются с линейными проводами, к которым подключаются фазы приемника. Ток в каждом из линейных проводов системы равен сумме двух токов, положительные направления которых противоположны (см. рис. 3.9). На основании сказанного ясно, что результирующие, токи линейных проводах равны векторной разности соответствующих фазных токов: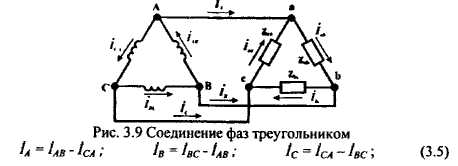



В этой системе три фазных напряжения будут вместе с тем линейными, поэтому как линейные, так и фазные токи, ими создаваемые, обозначают двумя индексами узлов («начал» обмоток генератора или фаз приемника).

Три линейных напряжения U_AB, U_BC и U_CAмогут быть исходными при построении векторной диаграммы системы (рис. 10а). Углы между ними равны 120°. Векторы фазных токов I_AB, I_BC, I_CA симметричной нагрузке сдвинуты по отношению создающим их напряжениям на некоторый угол φ значение которого зависит от отношения реактивного и активного сопротивлений приемника.

На основании соотношений (3.5), чтобы построить вектор линейного тока I_л.нужно к I_ABприбавить (—I_CA), т. е. вектор, равный по I_CA величине, но противоположный ему по направлению. На этом же основании определяются и два остальных линейных тока.

При симметричной нагрузке фазные токи по величине одинаковы: I_AB = I_BC - 1_фи должны быть равны между собой линейные токи I_A = I_B = I_C = I_л-

На диаграмме векторы фазных и линейных токов образуют три равнобедренных треугольника с острыми углами по 30" и тупым углом 120°. В таком треугольнике, опустив из вершины угла перпендикуляр на противолежащую сторону (рис. 3.10 6), найдем, что



Следовательно, в трехфазной симметричной системе, соединенной треугольником, фазные напряжения являются одновременно линейными: U_φΔ= U_лΔ, а линейные токи больше фазных в √5 раз: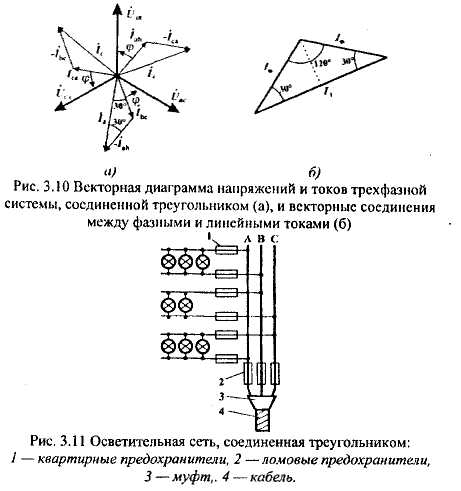





Некоторым преимуществом соединения фаз треугольником является то, что при несимметричной нагрузке нет необходимости использовать четвертый провод. На рис. 3.11 показана схема осветительной сети жилого дома при соединении фаз приемников треугольником.

Приемники подключаются к трем проводам трехфазной сети, причем они могут быть соединены звездой или треугольником независимо от способа соединения фаз генератора, питающего сеть.

В ряде случаев целесообразно в зависимости от условий работы приемников изменять способ соединения фаз — переключать фазы приемника от звезды на треугольник и обратно. Такое переключение применяется для уменьшения пусковых токов трехфазных электродвигателей, для изменения температуры трехфазных электрических печей, для изменения вторичных напряжений трансформаторов.

При переключении со звезды, на треугольник фаз симметричных приемников, сопротивления которых не зависят от напряжения, линейные токи увеличиваются в три раза:



но фазные токи возрастают в √5 раз:


3.4. МОЩНОСТЬ ТРЕХФАЗНОЙ СИСТЕМЫ И ЕЕ ИЗМЕРЕНИЕ
Активная мощность трехфазной системы Р является суммой фазных активных мощностей, а для каждой из них справедливо основное выражение активной мощности цепей переменного тока. Следовательно, фазная активная мощность Рф = 3U_фI_фcosφи при симметричной нагрузке активная мощность трехфазного устройства
Р = ЗР_Ф = 3 U_фI_фcosφ(3.7)
Но в трехфазных установках в большинстве случаев приходится выражать активную мощность устройства не через фазные, а через линейные величины. Это легко сделать на основании соотношений фазных и линейных величин, заменив в выражении активной мощности фазные величины линейными. При соединении звездой U_ф = U_л / √3 ; 1_Ф= I_л, а при соединении треугольником U_ф = U_ji; I_ф= I_л/√3 .После подстановки этих выражений в формулу (3.7) получим одно и то же выражение для активной мощности трехфазной симметричной установки:



Хотя это выражение относится только к активной мощности симметричной системы, тем не менее им можно руководствоваться в большинстве случаев, так как в промышленных устройствах основная нагрузка редко бывает несимметричной.

Реактивная мощность в симметричной системе, так же как и полная мощность, выражается через линейные величины подобно активной мощности: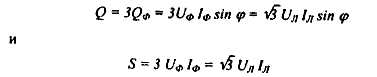



Простейшие условия измерения активной мощности трехфазной системы имеются в том случае, если фазы приемников соединены звездой с доступной нейтральной точкой. В этом случае для измерения мощности одной фазы цепь тока ваттметра соединяют последовательно с одной из фаз приемника (рис. 3.12 а), а цепь напряжения включают под напряжение той фазы приемника, в которую включена цепь тока ваттметра, т. е. зажимы цепи напряжения ваттметра присоединяются один к линейному проводу, а второй—к нейтральной точке приемника. В подобных условиях измеренная мощность



а мощность симметричного приемника



Часто нейтральная точка недоступна или фазы приемника соединены треугольником. Тогда применяется измерение с помощью искусственной нейтральной точки (рис. 12 6).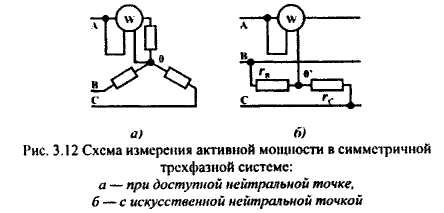



Такая точка (точнее узел) составляется из цепи напряжения ваттметра с сопротивлением r_nm-nи двух добавочных резисторов С такими же сопротивлениями. При таком соединении цепь напряжения ваттметра находится под фазным напряжением, а через цепь тока прибора проходит фазный ток. Следовательно, и при таком измерении



Для измерения активной мощности в четырехпроводной установке (т. е. установке с нейтральным проводом) при несимметричной нагрузке применяют способ трех ваттметров (рис. 3.13). В такой установке каждый из ваттметров измеряет активную мощность одной фазы, а активная мощность установки определяется как сумма мощностей, измеренных тремя ваттметрами: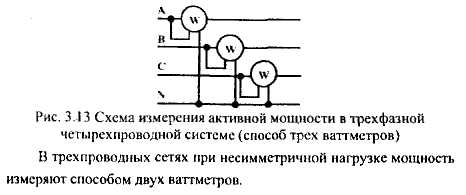



Если включить два ваттметра в трехпроводную систему постоянного тока (рис. 3.14), то они будут измерять мощность всей установки. При этом не имеет знамения, каковы напряжения отдельных пеней, объединенных в трехпроводную систем. Если вместо постоянных тока и напряжения рассматривать мгновенные значения напряжений и токов трехфазной системы, то в таких условиях ваттметры будут показывать средние значения мгновенных мощностей, т. е. активные мощности. Но следует иметь в виду, что хотя Р = Р₁+ Р₂, мощность системы равна сумме показаний двух ваттметров, но эта сумма алгебраическая, т. е. показание одного из ваттметров может быть отрицательным — стрелка одного из ваттметров может отклоняться в обратную сторону, за нуль шкалы. Чтобы отсчитать в таких условиях показание ваттметра нужно переключить зажимы цепи напряжения. Показания прибора после такого переключения следует считать отрицательными.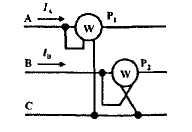



Рис. 3.14 Схема измерения активной мощности в трехфазной трехпроводной системе (способ двух ваттметров)
Пример. Трехфазный симметричный потребитель электроэнергии с сопротивлением фаз Za= Zь = Zc= Zф = R= 10 Ом соединен «звездой» и включен в трехфазную сеть с симметричным линейным напряжением Uл = 220 В (рис.3.15). Определить токи в фазных и линейных проводах, а также потребляемую активную мощность в режимах:

а) при симметричной нагрузке;

б) при отключении линейного провода;

в) при коротком замыкании той же фазы нагрузки.

Построить для всех трех режимов токографические диаграммы напряжений и показать на них вектора токов.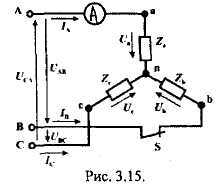



а) Решение. Фазные напряжения при симметричной нагрузке; Ua= Ub= Uc = Uф= Uл/√З = 220/√3 = 127 В. Фазные токи при этой нагрузке: I_Ф = U_ф/R_ф = 127/10 = 12,7 А. Линейные токи при симметричной нагрузке: I_A = I_С = Iл = Iф = 12,7 А, так как симметричный трехфазный потребитель электроэнергии соединен «звездой».

Активная мощность трехфазного симметричного потребителя: Р = ЗР_ф = ЗU_ф 1_фcosφ = 3*127*12,7* 1 = 4850 Вт = 4,85 кВт или Р = √5 U_л I_л соs φ _{_ф} = √3*220*12,7*1 = 4850 Вт= 4,85 кВт, где cosφ _{_ф} = 1 при Z_ф = R_ф.

Векторная диаграмма напряжений и токов приведена на рис.3.16.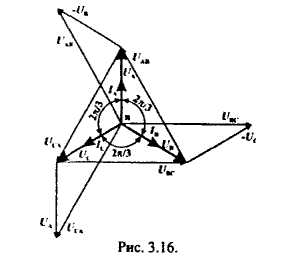



б)Решение Ток в линейных проводах аА и сС при обрыве линейного провода ЬВ (выключатель S разомкнут); так как сопротивление фазы Z_b= ∞ (1_В= 0), a Za= Rи Zс = Rвключены последовательно на линейное напряжение U_Ca =Uл = 220 В; I_A=1_С = I= U_cA/(R+ R) = 220/(10 + 10) = 11 А.

Напряжение на фазах потребителя при обрыве линейного провода bВ (нейтральная точка и в этом случае соответствует середине вектора линейного напряжения U_CA): Ua= Uc = U_CA/2 = 220/2=110 В.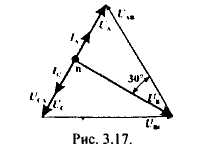



Напряжение между проводом фазы В и нейтральной точкой п определяют из векторной диаграммы (рис. 3.17): Uc = Uл cos pi/6 = 220* 0.866 = 190,5 В.

Активная мощность потребителя при обрыве линейного провода bВ: P = P_A + Р_C = 2I² R_ф = 2*11^2*10 = 2420 Вт= 2,42 кВт.

в) Для условия задачи определить фазные напряжения U_фи токи 1_Ф, активную мощность Рк потребителя при коротком замыкании фазы Zb, построить векторную диаграмму для этого случая рис. 3.18.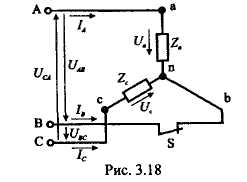



Решение. В данном случае Zb = 0 и Ub = 0, нейтральная точка п переместится в точку В, при этом фазные напряжения Uc= U_BC, U_A = Uав, т.е. фазные напряжения равны линейным напряжениям (U_ф= U_л). При этом фазные токи: I_A= I_c = Uл/R= 220/10 = 22 А. Ток 1_Впри коротком замыкании в соответствии с первым законом Кирхгофа для нейтральной точки n: I_A + I_B + I_C= О или -I_B = I_A + I_с.

Из прямоугольного треугольника на векторной диаграмме рис. 3.19 имеем: (-I_B/2)² + (I_A/2)² = I²_А, откуда I_B = √3 I_A = √5 • 22 = 38 A. При этом 1_А= Uл/Za = I_C = Uл/Zc = Uл/R = 220/10 = 22 А.

Активная мощность цепи при коротком замыкании: Р_к = Р_A + Р_C= 2 *I^2:_ф* R= 2 * 222 * 10 = 9680 Вт = 9,68 кВт. Векторная диаграмма напряжений и токов приведена на рис. 3.19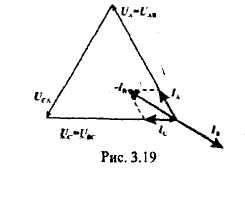