Курс лекций Теплотехника Раздел I. Техническая термодинамика Тема Введение. Основные понятия и определения Введение Термодинамическая система
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
Тема 12.Теплопередача12.1. Теплопередача через плоскую стенкуТеплопередачей называется передача теплоты от горячего теплоносителя к холодному теплоносителю через стенку, разделяющую эти теплоносители. Примерами теплопередачи являются: передача теплоты от греющей воды нагревательных элементов (отопительных систем) к воздуху помещения; передача теплоты от дымовых газов к воде через стенки кипятильных труб в паровых котлах; передача теплоты от раскаленных газов к охлаждающей воде (жидкости) через стенку цилиндра двигателя внутреннего сгорания; передача теплоты от внутреннего воздуха помещения к наружному воздуху и т. д. При этом ограждающая стенка является проводником теплоты, через которую теплота передается теплопроводностью, а от стенки к окружающей среде конвекцией и излучением. Поэтому процесс теплопередачи является сложным процессом теплообмена. При передаче теплоты от стенки к окружающей среде в основном преобладает конвективный теплообмен, поэтому будут рассматриваться такие задачи. 1). Теплопередача через плоскую стенку. Рассмотрим однослойную плоскую стенку толщиной и теплопроводностью (рис12.1). 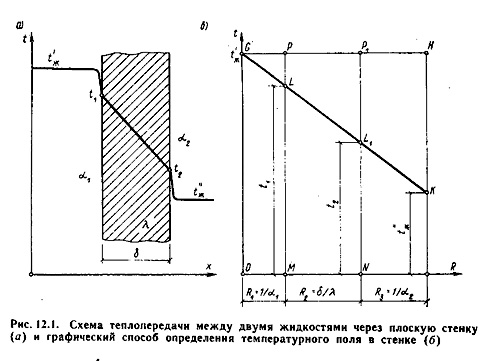 Температура горячей жидкости (среды) t'ж, холодной жидкости (среды) t''ж. Количество теплоты, переданной от горячей жидкости (среды) к стенке по закону Ньютона-Рихмана имеет вид: Q = 1 · (t'ж – t1) · F, (12.1) где 1 – коэффициент теплоотдачи от горячей среды с температурой t'ж к поверхности стенки• с температурой t1; F – расчетная поверхность плоской стенки. Тепловой поток, переданный через стенку определяется по уравнению: Q = / · (t1 – t2) · F. (12.2) Тепловой поток от второй поверхности стенки к холодной среде определяется по формуле: Q = б2 · (t2 - t''ж) · F, (12.3) где 2 – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t''ж. Решая эти три уравнения получаем: Q = (t'ж – t''ж) • F • К, (12.4) где К = 1 / (1/1 + / + 1/2) – коэффициент теплопередачи, (12.5) или R0 = 1/К = (1/1 + / + 1/2) – полное термическое сопротивление теплопередачи через однослойную плоскую стенку. (12.6) 1/1, 1/2 – термические сопротивления теплоотдачи поверхностей стенки; / - термическое сопротивление стенки. Для многослойной плоской стенки полное термическое сопротивление будет определяться по следующей формуле: R0 = (1/1 + 1/1 + 2/2 + … + n/n +1/2), (12.7) а коэффициент теплопередачи: К = 1 / (1/1 + 1/1 + 2/2 + … + n/n +1/2), (12.8) 12.2. Теплопередача через цилиндрическую стенкуПринцип расчета теплового потока через цилиндрическую стенку аналогична как и для плоской стенки. Рассмотрим однородную трубу (рис.12.2) с теплопроводностью , внутренний диаметр d1, наружный диаметр d2, длина l. Внутри трубы находится горячая среда с температурой t'ж, а снаружи холодная среда с температурой t''ж. 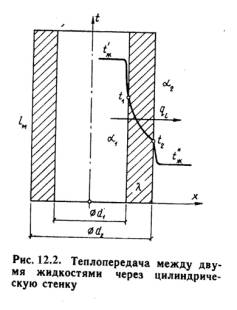 Количество теплоты, переданной от горячей среды к внутренней стенке трубы по закону Ньютона-Рихмана имеет вид: Q = ·d1·1·l·(t'ж – t1) , (12.9) где 1 – коэффициент теплоотдачи от горячей среды с температурой t'ж к поверхности стенки• с температурой t1; Тепловой поток, переданный через стенку трубы определяется по уравнению: Q = 2···l·(t1 – t2) / ln (d2/d1). (12.10) Тепловой поток от второй поверхности стенки трубы к холодной среде определяется по формуле: Q = ·d2·2·l·(t1 - t''ж) , (12.11) где 2 – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t''ж. Решая эти три уравнения получаем: Q = l·(t'ж – t''ж) • К, (12.12) где Кl = 1/[1/(1d1)+ 1/(2ln(d2/d1) + 1/(2d2)] – (12.13) - линейный коэффициент теплопередачи, или Rl = 1/ Кl = [1/(1d1)+ 1/(2ln(d2/d1) + 1/(2d2)] – (12.14)
теплопередачи через однослойную цилиндрическую стенку. 1/(1d1), 1/(2d2) – термические сопротивления теплоотдачи поверхностей стенки; 1/(2ln(d2/d1) - термическое сопротивление стенки. Для многослойной (n слоев) цилиндрической стенки полное линейное термическое сопротивление будет определяться по следующей формуле: Rl = 1/ Кl = [1/(1d1)+ 1/(21ln(d2/d1) + 1/(23ln(d3/d2) + … + 1/(2nln(dn+1/dn) + 1/(2dn)] – (12.15) 12.3. Типы теплообменных аппаратовТеплообменным аппаратом называют всякое устройство, в котором одна жидкость — горячая среда, передает теплоту другой жидкости - холодной среде. В качестве теплоносителей в тепловых аппаратах используются разнообразные капельные и упругие жидкости в самом широком диапазоне давлений и температур. По принципу работы аппараты делят на регенеративные, смесительные и рекуперативные. В регенеративных аппаратах горячий теплоноситель отдает свою теплоту аккумулирующему устройству, которое в свою очередь периодически отдает теплоту второй жидкости - холодному теплоносителю, т. е. одна и та же поверхность нагрева омывается то горячей, то холодной жидкостью. В смесительных аппаратах передача теплоты от горячей к холодной жидкости происходит при непосредственном смешении обеих жидкостей, например смешивающие конденсаторы. Особенно широкое развитие во всех областях техники получили рекуперативные аппараты, в которых теплота от горячей к холодной жидкости передается через разделительную стенку. Только такие аппараты будут рассмотрены в дальнейшем. Теплообменные аппараты могут иметь самые разнообразные назначения — паровые котлы, конденсаторы, пароперегреватели, приборы центрального отопления и т. д. Теплообменные аппараты в большинстве случаев значительно отличаются друг -от друга как по своим формам и размерам, так и по применяемым в них рабочим телам. Несмотря на большое разнообразие теплообменных аппаратов, основные положения теплового расчета для них остаются общими. В теплообменных аппаратах движение жидкости осуществляется по трем основным схемам. Если направление движения горячего и холодного теплоносителей совпадают, то такое движение называется прямотоком (рис.12.3,а). 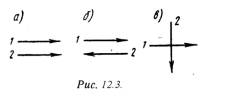 Если направление движения горячего теплоносителя противоположно движению холодного теплоносителя, то такое движение называется противотоком (рис.12.3,б). Если же горячий теплоноситель движется перпендикулярно движению холодного теплоносителя, то такое движение называется перекрестным током (рис.12.3,в). Кроме этих основных схем движения жидкостей, в теплообменных аппаратах применяют более сложные схемы движения, включающие все три основные схемы. 12.4. Расчет теплообменных аппаратовЦелью теплового расчета является определение поверхности теплообмена, а если последняя известна, то целью расчета является определение конечных температур рабочих жидкостей. Основными расчетными уравнениями теплообмена при стационарном режиме являются уравнение теплопередачи и уравнение теплового баланса. Уравнение теплопередачи: Q = k·F·(t1 – t2 ) , где Q — тепловой поток, Вт, k - средний коэффициент теплопередачи, Вт/(м2град), F — поверхность теплообмена в аппарате, м2, t1 и t2 - соответственно температуры горячего и холодного теплоносителей. Уравнение теплового баланса при условии отсутствия тепловых потерь и фазовых переходов: Q = = m1 ·t1 = m2·t2 , или Q = V11·cр1·(t/1 - t//1) = V2 2·cр2 ·(t//2 - t/2), (12.16) где V11,V2 2 - массовые расходы теплоносителей, кг/сек, с cр1 и cр2 - средние массовые теплоемкости жидкостей в интервале температур от tґ до t//, t/1 и t//1 температуры жидкостей при входе в аппарат; t/2 и t//2 - температуры жидкостей при выходе из аппарата. Величину произведения V··cр = W, Вт/град называют водяным, или условным, эквивалентом. С учетом последнего уравнение теплового баланса может быть представлено в следующем виде: (t/1 - t//1) / (t//2 - tґ2) = W2 / W1 , (12.17 ) W2 , W1 - условные эквиваленты горячей и холодной жидкостей. При прохождении через теплообменный аппарат рабочих жидкостей изменяются температуры горячих и холодных жидкостей. На изменение температур большое влияние оказывают схема движения жидкостей и величины условных эквивалентов. На рис.12.4 представлены температурные графики для аппаратов с прямотоков, а на рис.12.5 для аппаратов с противотоком. 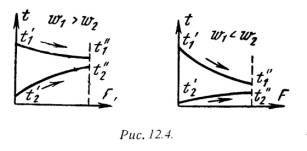 Как видно из рис.12.4 , при прямотоке конечная температура холодного теплоносителя всегда ниже конечной температуры горячего теплоносителя. При противотоке (рис.12.5) конечная температура холодной жидкости может быть значительно выше конечной температуры горячей жидкости. Следовательно, в аппаратах с противотоком можно нагреть холодную среду, при одинаковых начальных условиях, до более высокой температуры, чем в аппаратах с прямотоком. Кроме того, как видно из рисунков, наряду с изменениями температур изменяется также и разность температуря между рабочими жидкостями, или температурный напор t. 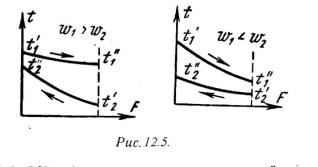 Величины t и k можно принять постоянными только в пределах элементарной поверхности теплообмена dF. Поэтому уравнение теплопередачи для элемента поверхности теплообмена dF справедливо лишь в дифференциальной форме: dQ==k·dF·t . (12.18) Тепловой поток, переданный через всю поверхность F при постоянном среднем коэффициенте теплопередачи k, определяется интегрированием уравнения (12. ): Q = k·dF·t= k·F·tср , (12.19) где tср - средний логарифмический температурный напор по всей поверхности нагрева. Для случаев, когда коэффициент теплопередачи на отдельных участках поверхности теплообмена значительно изменяется, его усредняют: kср = (F1·k1 + F2·k2 + … + Fn·kn) / (F1 + F2 + … + Fn). Тогда при kср = const уравнение (12.9 ) примет вид Q = kср t ·dF = kср ·tср ·F. (12.20) Если температура теплоносителей изменяется по закону прямой линии (рис.12.6, пунктирные линии), то средний температурный напор в аппарате равен разности среднеарифметических величин: tср = (t/1 + t//1)/2 - (t//2 + t/2)/2 . (12.21) 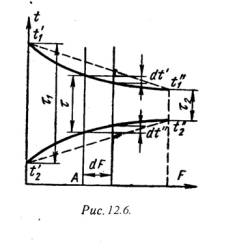 Однако температуры рабочих жидкостей меняются по криволинейному закону. Поэтому уравнение (12.21) будет только приближенным и может применяться при небольших изменениях температуры обеих жидкостей. При криволинейном изменении температуры величину tср называют среднелогарифмическим температурным напором и определяется по формулам: для аппаратов с прямотоком tср = [(t/1 - t/2) - (t//1 - t//2)] / ln[(t/1 - t/2)/(t//1 - t//2)] . (12.22) для аппаратов с противотоком tср = [(t/1 - t//2) - (t//1 - t/2)] / ln[(t/1 - t//2)/(t//1 - t/2)] . (12.23) Численные значения tср для аппаратов с противотокм при одинаковых условиях всегда больше tср для аппаратов с прямотоком, поэтому аппараты с противотокм имеют меньшие размеры. Литература
|
