Курсовая работа по основам научных исследований (укр. язык). Курсова робота з дисципліни Основи наукових досліджень за темою Моделювання напруженого стану волокнистих композиційних матеріалів
 Скачать 434 Kb. Скачать 434 Kb.
|
|
М  іністерство освіти і науки України іністерство освіти і науки України Чернігівський національний технологічний університет Кафедра технологій машинобудування і деревообробки КУРСОВА РОБОТА з дисципліни «Основи наукових досліджень» за темою: Моделювання напруженого стану волокнистих композиційних матеріалів Керівник к.т.н., доцент Сапон С.П. Виконавець Міщенко І. М. Чернігів – 2018 ЗМІСТ 1.АКТУАЛЬНІСТЬ ТЕМИ ДОСЛІДЖЕННЯ 3 2.ОГЛЯД СУЧАСНОГО СТАНУ ПРОБЛЕМИ ВИЗНАЧЕННЯ НАПРУЖЕНО-ДЕФОРМОВАНОГО СТАНУ КОНСТРУКЦІЙ ІЗ ВОЛОКНИСТИХ КОМПОЗИЦІЙНИХ МАТЕРІАЛІВ 5 2.1 Типи волокнистих композиційних матеріалів 5 2.2 Основні тенденції розвитку методів визначення пружних характеристик композиційного матеріалу 6 2.3 Методи розрахунку конструкцій із волокнистих композиційних матеріалів 16 3.ПОСТАНОВКА МЕТИ І ЗАДАЧ ДОСЛІДЖЕННЯ 21 ПЕРЕЛІК ПОСИЛАНЬ 22 АКТУАЛЬНІСТЬ ТЕМИ ДОСЛІДЖЕННЯКомпозиційні матеріали різної структури мають суттєві переваги в порівнянні з традиційними матеріалами завдяки широкому варіюванню властивостей у межах окремих структурних груп. Завдяки високій міцності, низькій вазі, малій вартості, а також простотій технології виготовлення композиційні матеріали широко використовуються для створення сучасних конструкційних матеріалів та ефективної техніки на їх основі в таких галузях як машино-, судно- та літакобудування, транспорт, будівництво, космічна, медична галузь тощо. В процесі експлуатації в елементах конструкції сучасної техніки виникають температурні напруження та деформації, змінюються фізико-механічні характеристики, що може впливати на міцність, довготривалість та інші механічні якості конструкції. В процесі проектування конструкцій на основі волокнистих композитів проводиться попередній розрахунок деформаційних, міцнісних та інших характеристик конструкцій. Аналіз цих розрахунків надалі уможливлює коригування конструктивних особливостей шляхом зміни механічних властивостей композита та параметрів конструкції (розміру, форми тощо). Процес проектування конструкцій із використанням волокнистих композитів дає додаткові можливості для керування механічними властивостями композита за рахунок варіювання марками матеріалів матриці та волокна, розмірами волокон, характеристиками армування (напрямом, частотою, схемою укладки) тощо. Для раціонального вибору вищезазначених параметрів необхідно якомога точніше визначити компоненти напружено-деформованого стану конструкцій у реальних умовах експлуатації. Дослідження фізико-механічних характеристик та характеру руйнування композитних матеріалів під дією експлуатаційних навантажень на стадії проектування технічних систем забезпечує достовірне визначення ресурсу майбутніх деталей та вузлів. Існує значна кількість механічних аспектів, які необхідно враховувати при дослідженні волокнистих композиційних матеріалів. Зокрема, однією з основних проблем при розв’язанні задач механіки композитів є адекватне визначення пружних властивостей композиційного матеріалу. При реалізації цього завдання найпоширенішою тенденцією є врахування специфічних властивостей матриці та волокна (анізотропії, пластичності, в’язкопружності та інших) при визначенні властивостей композита, а також урахування особливостей їх сумісного деформування (наявність перехідного шару, адгезії тощо). Процес розрахунку напружено-деформованого стану конструкцій із композитів без урахування анізотропних властивостей волокна та матриці не завжди дає адекватні результати. Аналітичні методи дозволяють отримувати точні розв’язки, але за їх допомогою можливо визначати напружено-деформований стан конструкцій лише простої геометрії. Чисельні методи, такі як метод скінченних елементів, метод кінцевих різниць, метод граничних елементів та інші, дозволяють знаходити розв’язки для конструкцій із складною геометрію та будь-якими граничними умовами, але актуальним стає питання точності наближених результатів. Тому процедура вибору методу дослідження є важливою з точки зору адекватності отриманих результатів. ОГЛЯД СУЧАСНОГО СТАНУ ПРОБЛЕМИ ВИЗНАЧЕННЯ НАПРУЖЕНО-ДЕФОРМОВАНОГО СТАНУ КОНСТРУКЦІЙ ІЗ ВОЛОКНИСТИХ КОМПОЗИЦІЙНИХ МАТЕРІАЛІВ2.1 Типи волокнистих композиційних матеріалівКомпозиційні матеріали представляють собою з’єднання двох або більше компонентів в загальній системі, в якій кожен компонент зберігає свої властивості [26]. Композити можна розглядати як в макро-, так і в мікромасштабах. У зв’язку з цим їх можна представити як однорідні або неоднорідні відповідно. Неперервний компонент у всьому об’ємі композиційного матеріалу називають матрицею, а роз’єднаний в об’ємі композиції − арматурою або армуючим елементом. Композиційні матеріали можуть бути розділені за кількома основними ознаками [28]: за матеріалом матриці і армуючих компонентів; за структурою геометрії (морфології) і розташуванню компонентів (структурних складових); за методом отримання; за областю застосування. Однак існує і інша класифікація у відповідності до морфології фаз, що складають їх мікроструктуру або геометрією компонентів: волокнисті композиційні матеріали; ламіновані (шаруваті) композиційні матеріали; дисперсно-зміцнені композиційні матеріали; комбінація з деяких або всіх з перших трьох типів. Залежно від геометрії армуючих елементів та їх взаємного розташування композиційні матеріали поділяють на ізотропні та анізотропні [26]. Перші мають однакові властивості у всіх напрямах, тоді як властивості анізотропних залежать від напряму. Ортотропні матеріали характеризуються наявністю в кожному елементарному об’ємі трьох взаємно перпендикулярних площин симетрії властивостей. До таких матеріалів відносяться композиційні матеріали, що армовані шарами волокон, які послідовно чергуються та тканини з поздовжньо-поперечною укладкою. Одним із основних завдань механіки композиційних матеріалів є визначення механічних характеристик композита за властивостями його компонентів. Елементи конструкцій з композиційних матеріалів складаються зазвичай з односпрямованих армованих шарів, покладених в певній послідовності, тому в основі методів розрахунку і проектування таких конструкцій лежать механічні характеристики односпрямованого армованого шару, які потрібно визначити експериментально або шляхом розрахунку. Механічна поведінка окремих композитів значно залежить від часу, що обумовлено суттєво вираженими в’язкопружними властивостями полімерних сполучень і деяких типів волокон. Працездатність і довговічність конструкцій із композитних матеріалів, що знаходяться в умовах інтенсивних теплових впливів, залежить, зокрема, від ефективних коефіцієнтів теплового розширення, які дозволяють оцінювати зміни геометричних розмірів тіла при зміні температури. 2.2 Основні тенденції розвитку методів визначення пружних характеристик композиційного матеріалуДо визначення пружних характеристик композиційного матеріалу за пружними характеристикам його складових існує два альтернативних підходи. Згідно з першим підходом, експериментально досліджується певний структурний елемент композита, який містить достатньо велику кількість армуючих частинок, щоб результати, отримані для нього, можна було б узагальнити на будь-який об’єм композиційного матеріалу. Застосування такого підходу дозволяє врахувати зміну пружних властивостей матриці й армуючих волокон в процесі виготовлення композита. З іншого боку, для отримання композита з необхідними властивостями доводиться проводити велику кількість експериментів, варіюючи різними параметрами – такими, як об’ємний вміст арматури, характер розташування армуючих елементів, застосування різних матеріалів для матриці та армуючих волокон. Альтернативний структурний підхід передбачає визначення пружних характеристик композита через пружні характеристики матриці та армуючих волокон, їх об’ємні частки в композиті, розміри та взаємне розташування армуючих елементів. Суттєвим недоліком такого підходу є те, що пружні характеристики структурних складових можуть значно відрізнятися у вихідному стані і в композиті. В цілому композит можна представити як матеріал з анізотропними властивостями. Зв’язок між напруженнями та деформаціями для анізотропного матеріалу описується узагальненим законом Гука: де – σij компоненти тензора напружень, εkl – компоненти тензора деформацій, Cijkl – компоненти тензора пружних сталих. Таким чином, для описання пружних властивостей композиційного матеріалу необхідно знати 81 компоненту тензора Cijkl. Різних компонент для анізотропного матеріалу залишається всього 21 [1], якщо враховувати, що коефіцієнти тензора пружних сталих мають симетрію відносно індексів i, j, k, l: А враховуючи, що волокнистий композиційний матеріал являє собою односпрямований армований шар (рис. 2.1), його можна розглядати як ортотропне середовище, що визначається 9 незалежними пружними сталими. 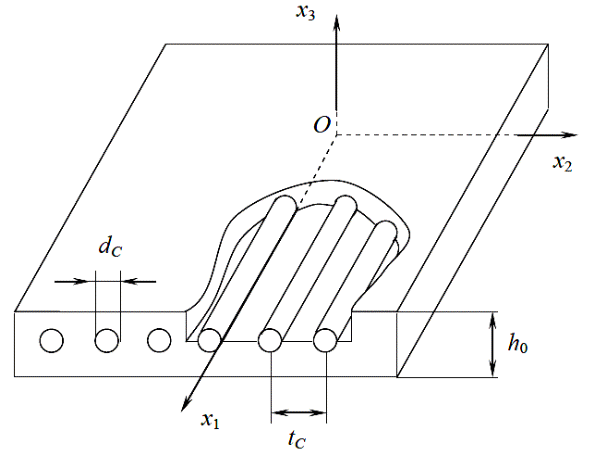 Рисунок 2.1 – Елементарний односпрямований армований шар Для ортотропного матеріалу закон Гука запишеться в такому вигляді:  (2.3) (2.3)де aij– компоненти тензора податливості. Якщо перейти від компонентів тензора податливості до технічних сталих, то рівняння (2.3) запишуться у вигляді: 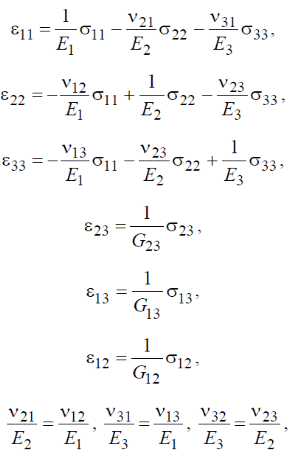 (2.4) (2.4)де E1, E2,E3, – модулі пружності в напрямі осей x1, x2, x3; G23, G13, G12 – модулі зсуву в площинках x1x3, x2x3, x1x2; νij (ji=1, 2, 3,i≠j) – коефіцієнти Пуассона, котрі характеризують поперечне стискання при розтягненні в напрямі осей координат (визначають скорочення в напряму осі xj(другий індекс)при розтягненні вздовж осі xі(перший індекс). Враховуючи напрям армування (рис. 2.1) E1 називають поздовжнім модулем пружності, а E2,E3 - поперечними модулями пружності, аналогічно модулі G13, G12 називають модулями поздовжнього зсуву, а G23 – модулем поперечного зсуву. Найбільш поширені методики визначення пружних сталих для композиційного матеріалу дають такі співвідношення. Розглянемо спочатку пружні сталі, отримані для плоскої задачі теорії пружності. В роботі Лапіна О.А. [15] запропоновані такі співвідношення: 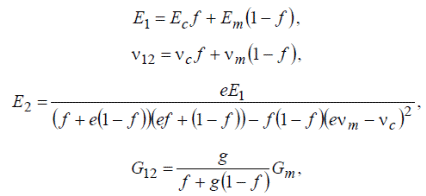 (2.5) (2.5)де Ec – модуль пружності матеріалу волокна; Em– модуль пружності матеріалу матриці; Gc– модуль зсуву матеріалу волокна, Gm– модуль зсуву матеріалу матриці, νc – коефіцієнт Пуассона матеріалу волокна; νm – коефіцієнт Пуассона матеріалу матриці; f– коефіцієнт армування, що характеризує відносний об’ємний вміст волокон. Для волокон круглого перетину й параметрів шару, зображеного на рис. 2.1, коефіцієнт армування визначається формулою [20]: 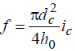 (2.5) (2.5)де dc– діаметр волокон; h0 – товщина армованого шару; ic– частота армування. В роботі [1] запропоновані такі співвідношення для визначення пружних сталих композиційного матеріалу: 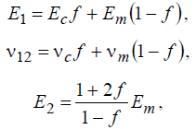 , , 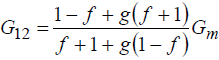 (2.6) (2.6)Для розв’язання тривимірних задач механіки композитів запропоновані такі співвідношення для визначення пружних сталих. В роботі [20] для найпростішої моделі композиційного матеріалу – системи жорстко зв’язаних почергових ізотропних стрижнів, які мають характеристики волокна та матриці – представлені співвідношення, отримані на основі рівняння адитивності або правила сумішей: 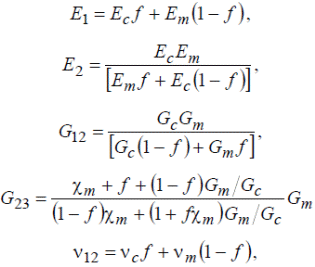 (2.7) (2.7)На основі точної теорії армування [18] запропоновані аналітичні вирази для пружних характеристик композиційного матеріалу з ізотропною матрицею та трансверсально-ізотропним волокном. В результаті отримані такі пружні сталі композита: 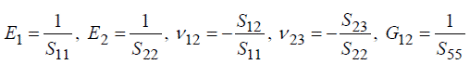 (2.8) (2.8)Пружні податливості обчислюються за формулами: 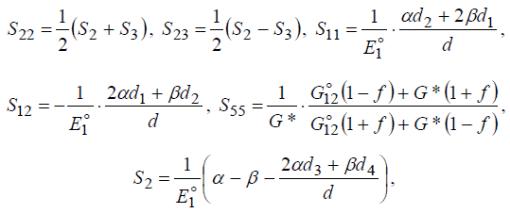 (2.9) (2.9)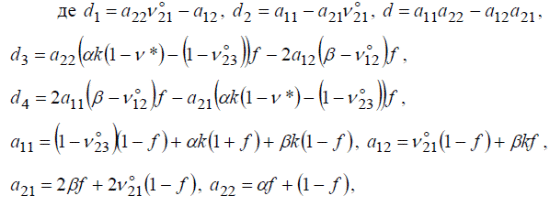 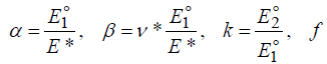 f – об’ємний вміст волокна, * – позначені величини, що відносяться до матриці, º – величини, що відносяться до волокна. Основними тенденціями при визначенні механічних характеристик композиційних матеріалів на сьогодні є спроби врахування особливих властивостей матеріалів матриці та волокна (анізотропії, в’язкопружності, температурного розширення, пластичності, слабкої стисливості та інших) та особливостей сумісного деформування матриці та волокна (контакту матеріалу матриці з матеріалом волокна, особливостей зчеплення між ними, наявності перехідного шару між матеріалами, дифузії, наявності пошкоджень тощо). Врахування зазначених особливостей приводить до створення громіздких математичних моделей, застосовувати до яких аналітичні методи, як правило, не вдається. При застосуванні цих моделей використовують наближені методи (асимптотичні, чисельні), котрі, як правило, дають не аналітичні співвідношення, а числові значення механічних характеристик. Так, широкого застосування набули асимптотичні підходи при визначенні ефективних механічних характеристик. Тут можна відзначити такі роботи. Основи варіаційного асимптотичного методу (VAMUCH) для визначення властивостей композитів, у тому числі й волокнистих, викладені в роботах Yu W. і Tang T. [43, 44, 46, 47]. Так, у монографії [43] наведено підходи до визначення пружно-пластичних, електромагнітопружних та інших властивостей композитів за допомогою варіаційного асимптотичного методу. Із зазначенням про періодичність армування як малий параметр, була сформульована варіаційна постановка для елементарної комірки гомогенізації за допомогою асимптотичного розкладання функціонала енергії. Для отримання чисельних результатів використовувався метод скінченних елементів, у результаті були визначені локальні поля в границях елементарної комірки, на основі яких можна відновити глобальну поведінку матеріалу. Перевагами методу є те, що за його допомогою визначаються властивості матеріалу за всіма напрямами одночасно в результаті розв’язання однієї задачі. У статті Yu W., Tang T. [47] описане застосування варіаційного асимптотичного метода для елементарної комірки гомогенізації для дослідження ефективних властивостей волокнистого композиційного матеріалу, а також напружено-деформованих полів на мікрорівні. У роботі Yu W., Tang T. [46] цей же метод використано для прогнозування ефективних термопружних властивостей композиційного матеріалу. На основі розробленої моделі та з використанням методу скінченних елементів отримані термопружні характеристики композита зі сферичними включеннями та композита с волокнами круглого й квадратного перетину. Інша стаття Tang T., Yu W. [44] також присвячена подібній тематиці – застосуванню варіаційного асимптотичного методу до визначення термопружних характеристик та характеристик теплопровідності бінарного композита, композита зі сферичними та циліндричними включеннями. В серії робіт [12, 13, 14] показано застосування методу асимптотичного осереднення до визначення пружних сталих волокнистого і тканинного композита. Так, в роботі Димитрієнка Ю.І., Соколова А.П. [14] викладені основи методу асимптотичного осереднення (методу Бахвалова-Побєдрі) для задач теорії пружності, а також основи методу скінченних елементів для розв’язання локальних задач теорії пружності на «комірці періодичності» та розрахунку ефективних пружних характеристик композитів. Надані варіаційні формулювання задач теорії пружності та задач на «комірці періодичності». Наведені приклади чисельних розв’язків локальних задач та результати моделювання полів мікронапружень для різних типів композиційних матеріалів: односпрямовано-армованих, просторово-ортогонально-армованих та інших. Розвиток методу асимптотичного осереднення періодичних структур на випадок багаторівневих ієрархічних структур для визначення ефективних пружних характеристик композиційних матеріалів надано в статті Димитрієнка Ю.І., Соколова А.П. [13]. Сформульовані рекурентні послідовності локальних та осереднених задач теорії пружності на комірках періодичності різних структурних рівнів. Наведено приклади скінченноелементних розв’язків серії локальних задач для моделі дворівневої структури тканинного композиційного матеріалу. Робота Димитрієнка Ю.І., Соколова А.П. [12] також присвячена розширенню методу асимптотичного осереднення періодичних структур на випадок багаторівневих ієрархічних структур. Запропоновано метод обчислення міцнісних властивостей композиційного матеріалу за міцнісними властивостями його компонентів. На основі методу скінченних елементів проведено міцнісний розрахунок тканинного композиційного матеріалу. Для регулярних неоднорідних структур, у тому числі волокнистих композитів, математичне моделювання їх фізико-механічної поведінки здійснюється рівняннями з швидко осцилюючими коефіцієнтами [4, 5]. Використання таких рівнянь для чисельного розв’язання задач є досить проблематичним навіть за наявності сучасної комп’ютерної техніки. Тому за допомогою розкладання визначальних функцій за малим параметром (розміром комірки періодичності тощо) асимптотичним методом осереднення будуються простіші рівняння з осередненими коефіцієнтами, які й використовуються для розв’язання низки задач. Асимптотичний підхід до визначення пружних та в’язкопружних характеристик волокнистого композита на комірці періодичності використано в роботі [9]. Застосовано розкладання шуканої функції за малим параметром (відношення розміру комірки періодичності до лінійного розміру всього зразка) для визначення фізико-механічних характеристик (коефіцієнти теплопровідності, дифузії, електропровідності тощо) волокнистих та зернистих композитів. У монографії Kwon Y.W., Allen D.H., Talreja R. [39] представлено широкий спектр методів із застосуванням імовірнісних та статистичних підходів, які дозволяють описувати механічну поведінку композитів, у тому числі волокнистих та нанокомпозитів. Розглядаються різні підходи до визначення пружних сталих при наявності пошкоджень, тріщин, дифузії, температурних факторів, реологічних процесів і т.ін. У тому числі наведено термопружні сталі для волокнистого композита, армованого системою n волокон. Zhong W., Pan N. [48] на основі методу Монте-Карло запропонували стохастичний підхід до дослідження міжфазних явищ у волокнистих композитах. Зокрема, запропоновані методики були використані для моделювання процесу порушення зчеплення волокна та матриці. Як правило, складність процесів взаємодії матриці та волокна приводить до складних математичних постановок задач, розв’язати які аналітичними методами не видається можливим. Тому використовують чисельні методи, такі як метод скінченних елементів, метод кінцевих різниць та інші. В дисертаційній роботі Бєлова Д.А. [6] для пружного односпрямованого волокнистого композитного матеріалу розроблені методи гомогенізації та гетерогенізації, які дозволяють проводити аналіз механічної поведінки композитів на мікрорівні (характерні розміри – діаметри волокон, відстані між волокнами тощо) та на макрорівні (характерними розмірами є розміри конструкції), здійснюючі переходи з мікрорівня на макрорівень (гомогенізація), а також із макрорівня на мікрорівень (гетерогенізація). На основі об’єднання МСЕ і методу Монте-Карло розроблено алгоритм визначення ефективних пружних характеристик стохастичних односпрямованих волокнистих композитних матеріалів. На сьогодні наявна певна кількість робіт довідкового, а іноді більш навчального характеру, в яких узагальнено на час їх видання технологічні, механічні, фізичні, хімічні, конструкторські та інші аспекти виробництва й експлуатації композиційних матеріалів, у тому числі волокнистих. Ці роботи мають різну міру деталізації тих чи інших аспектів, однак, незважаючи на це, всі вони можуть бути використані в інженерній справі при розрахунку та проектуванні композиційних матеріалів та конструкцій із них. Зокрема, різні групи співвідношень для визначення ефективних механічних характеристик волокнистого композита зведено в довідниках під редакцією Карпиноса Д.М. [20], Васильева В.В., Тарнопольського Ю.М. [19], Kelly A. [35] та інших. 2.3 Методи розрахунку конструкцій із волокнистих композиційних матеріалівПроблеми механіки руйнування та оптимального проектування конструкцій із композиційних матеріалів, у тому числі й волокнистих, розглядаються в монографії Черепанова Г.П. [33]. Узагальнення підходів та методів розв’язання задач механіки композитів наведено в літературі довідкового характеру. У довіднику під редакцією Карпиноса Д.М. [20] описані методи розрахунку фізико-механічних, міцнісних характеристик композиційних матеріалів, методи визначення їх складу та структури, наведено великий обсяг експериментальних даних. Довідник під редакцією Васильєва В.В., Тарнопольського Ю.М. [19] містить опис методів розрахунку напружено-деформованого стану різних конструкцій (балки, стрижні, кільця, труби, балони тиску, багатошарові конструкції та інші) із композиційних матеріалів. В короткій енциклопедії під редакцією Kelly A. [35] викладені основні дані про властивості та особливості механічної поведінки штучних та природних композитів, у тому числі волокнистих. Розвиток методів розрахунку неоднорідних конструкцій з анізотропними властивостями можна відзначити в роботах Сметанкіної Н.В. [30], Верещаки С.М., Дейнеки А.В., Данільцева В.В. [10], Карнаухова В.Г., Козлова В.І., Карнаухової Т.В. [16, 17] та інших. При розрахунку просторових конструкцій введенням спрощувальних гіпотез та припущень вдається зменшити розмірність задачі й звести тривимірні задачі до задач теорії пластин та оболонок. Тому спочатку розглянемо розв’язання задач механіки анізотропного середовища на основі теорії пластин та оболонок. Розрахунки на міцність армованих тонкостінних конструкцій (стрижневих конструкцій, пластин, оболонок, панелей) та принципи їх раціонального проектування представлені в роботі [25]. В роботі Mukhopadhyay М. [40] здійснена спроба викласти комплексний та єдиний підхід до аналізу ряду аспектів механіки склопластиків. Викладені різні теорії деформування конструкцій із таких матеріалів, зокрема балок, пластин тощо. Розглянуті особливості розв’язання задач статики, динаміки, термопружності та теплопровідності, механіки руйнування для склопластиків. Представлені основи методу скінченних елементів для розв’язання цих задач та чисельні результати розрахунків. У зв’язку з широким застосуванням конструкцій із композиційних матеріалів, наприклад, у автомобільній промисловості, набув розвитку такий напрям, як механіка багатошарових конструкцій. Алгоритми чисельного розв’язання задач статики шаруватих ортотропних і анізотропних оболонок Кірхгоффа–Лява розроблені Григоренком Я.М. і його учнями [11]. Значний внесок у розвиток теорії багатошарових пластин та оболонок внесли Амбарцумян С.А. [3], Рябов А.Ф. та Рассказов А.О. [29], Терегулов А.Г. [31] та інші. До цього напрямку дотичні дослідження пластин та оболонок із композиційних матеріалів: Бідермана В.Л. [7], Корольова В.І. [22] та інших. Розрахунок оболонкових конструкцій із застосуванням методу скінченних елементів та теорії рядів Фур’є проведено у [32]. Описано комплекс програм із розрахунку напружено-деформованого стану та дослідження стійкості складених багатошарових ортотропних оболонкових конструкцій при силових та температурних навантаженнях. За допомогою цього комплексу проведено дослідження напружено-деформованого стану тороподібної оболонки обертання змінної товщини та жорсткості. Робота Dvorak G. [36] представляє широкий спектр аналітичних та чисельних методів для моделювання властивостей та поведінки композиційних та шаруватих матеріалів, полікристалів та інших неоднорідних середовищ у різних умовах. Дослідження проводились на різних рівнях, починаючи від нано- (атоми) та мікрорівня (матриця, волокно), мезорівня (проміжний – армований шар, тканинні та шаруваті структури) і закінчуючи макрорівнем (гомогенізований матеріал). В монографії Matthews F.L., Davies G.A.O., Hitchings D., Soutis C. [38] викладені основні теоретичні відомості про волокнисті композиційні матеріали та про особливості застосування методу скінченних елементів до розрахунку конструкцій із них. Зокрема, особливу увагу приділено вивченню таких особливостей, як наявність отворів, крайові та міжшарові ефекти, розшарування тощо. Aboudi J., Arnold S.M., Bednarcyk B.A. [1] наводять методи, що дозволяють моделювати поведінку композиційних матеріалів у різних умовах деформування. Наведено відомості про застосування різних методів опису композиційних матеріалів на мікрорівні. Розглянуті моделі пружної, в’язкопружної, пружнопластичної, термопружної поведінки композитів, ряд моделей механіки руйнування. Монографія Tenek L.T., Argyris J. [45] містить основні відомості про чисельний аналіз тривимірних композитних конструкцій із використанням методу скінченних елементів. Розглянуті питання, що стосуються визначення напружено-деформованого стану балок, пластин і оболонок у лінійній та нелінійній постановці. В роботі Barbero E.J. [34] розглянуті особливості моделювання ряду ефектів, притаманних композиційним матеріалам, таких як крайові ефекти, розшарування, в’язкопружність тощо. Наведені чисельні результати розрахунків із використанням ANSYS та MATLAB. Складність постановок просторових задач обумовлює використання чисельних методів розв’язання тривимірних та двовимірних задач. До таких методів зараховують метод скінченних елементів, метод кінцевих різниць, метод граничних елементів тощо. Soares C.A.M., Soares C.M.M., Freitas M.J.M. [42] наводять основні теоретичні відомості про механіку композиційних матеріалів, основи методу скінченних елементів для розрахунку шаруватих композиційних балок, пластин та оболонок. Особливу увагу приділено оптимізації конструкцій із композиційного матеріалу, дослідженню різних видів руйнування таких конструкцій. Робота Gopalakrishnan S., Chakraborty A., Mahapatra D.R. [37] представляє собою системний виклад спектрального методу скінченних елементів для аналізу неоднорідних та анізотропних структур, у тому числі в контексті проблем механіки руйнування таких конструкцій. В монографії Ochoa O.O., Reddy J.N. [41] викладені основи методу скінченних елементів для розрахунку напружено-деформованого стану шаруватих пластин із композиційних матеріалів. Представлені моделі для дослідження нелінійної поведінки, динамічних задач, дослідження пошкоджень та критеріїв відмови таких конструкцій та ін. У роботі Марчука А.В. та Пискунова В.Г. [23] застосовано напіваналітичний метод скінченних елементів до розв’язання задач механіки композитів та розрахунку шаруватих конструкцій. Особливості застосування методу скінченних елементів до розв’язання задач механіки неоднорідних пологих оболонок та пластин шаруватої структури представлено у [27]. Залежно від типу задачі, що розглядається, та властивостей матеріалу конструкції доцільно використовувати матриці жорсткості скінченних елементів, які побудовані з урахуванням тих чи інших гіпотез та припущень. Одним із напрямків розвитку чисельних методів розрахунку просторових конструкцій із композиційних матеріалів є створення програмних комплексів для розрахунку ракетно-космічної техніки, що пов’язане з вирішенням актуальних задач міцності силових елементів конструкцій складної конфігурації. Сучасні вимоги до процесу проектування конструкцій потребують вдосконалення та розвитку систем автоматизованого проектування (САПР) чи САD (Computer-Aided Design) та систем автоматизації інженерних розрахунків і аналізу (САЕ) [24]. Найпоширеніші спеціалізовані програмні комплекси ANSYS, Abacus, Patran, Nastran широко застосовуються у практиці проектування ракетно-космічної техніки. Так, програмний комплекс скінченно-елементного аналізу Nastran [21] було використано при проектуванні конструктивних елементів ракети-носія «Циклон-4» із полімерних композитних матеріалів (ПКМ). При визначенні напружено-деформованого стану шаруватих конструкції або враховують наявність розривних властивостей матеріалу, або будують еквівалентну неперервну модель. ПОСТАНОВКА МЕТИ І ЗАДАЧ ДОСЛІДЖЕННЯМета роботи: здійснити моделювання напруженого стану волокнистих композиційних матеріалів. Для досягнення поставленої мети розв’язувалися наступні задачі: провести аналіз існуючих методик визначення напружено-деформованого стану конструкцій із волокнистих композиційних матеріалів; проаналізувати методи розрахунку конструкцій із волокнистих композиційних матеріалів; на основі методу скінчених елементів здійснити моделювання напружено-деформованого стану волокнистих композиційних матеріалів; розробити методику моделювання напружено-деформованого стану волокнистих композиційних матеріалів. Об’єкт дослідження процес моделювання напружено-деформованого стану волокнистих композиційних матеріалів. Предмет дослідження характеристики та компоненти напружено-деформованого стану композиційних матеріалів та конструкцій із них. ПЕРЕЛІК ПОСИЛАНЬAboudi J. Micromechanics of Composite Materials: A Generalized Multiscale Analysis Approach / J. Aboudi, S.M. Arnold, B.A. Bednarcyk. – Oxford: Butterworth-Heinemann, 2012. – 1006 p. Ashton J.E. Primer on composite materials: analysis / J.E. Ashton, J.C. Halpin, P.H. Petit. – Stamford: Technomic, 1969. – 124 p. Амбарцумян С.А. Теория анизотропных пластин: Прочность, устойчивость и колебания / С.А. Амбарцумян. – М.: Наука, 1987. –360 с. Бардзокас Д.И. Математическое моделирование физических процессов в композиционных материалах периодической структуры / Д.И. Бардзокас, А.И. Зобнин. – М.: Едиториал УРСС, 2003. – 376 с. Бахвалов Н.С. Осреднение процессов в периодических средах. Математические задачи механики композиционных материалов / Н.С. Бахвалов, Г.П. Панасенко. – М.: Наука. Главная редакция физико-математической литературы, 1984. – 352 с. Белов Д.А. Гомогенизация и гетерогенизация однонаправленных упругих волокнистых композитов: дис. … кандидата тех. наук: 01.02.06 / Д.А. Белов. – СПб.: ГОУВПО «Санкт-Петербургский государственный политехнический университет», 2009. – 195 с. Бидерман В.Л. Пластинки и оболочки из стеклопластиков / В.Л. Бидерман // Прочность, устойчивость, колебания. – М.: Машиностроение. – 1968. – Т. 2. – С. 211-242. Блох В.И. Теория упругости / В.И. Блох. – Харьков: изд-во Харьковского университета, 1964. – 483 с. Большаков В.И. Асимптотические методы расчета композитных материалов с учетом внутренней структуры / В.И. Большаков, И.В. Андрианов, В.В. Данишевский. – Днепропетровск: «Пороги», 2008. – 196 с. Верещака С.М. Термопружний напружений стан склопластикового шарнірно обпертого циліндра з урахуванням неідеального контакту між шарами / С.М. Верещака, А.В. Дейнека, В.В. Данільцев // Вісник Запорізького національного університету. Фізико-математичні науки, №3, 2015. – С. 42-50. Григоренко Я.М. Изотропные и анизотропные слоистые оболочки вращения переменной жесткости / Я.М. Григоренко. – К.: Наук. думка, 1973. – 228 с. Димитриенко Ю.И. Исследование процессов разрушения композиционных материалов на базе метода асимптотической гомогенизации / Ю.И. Димитриенко, А.П. Соколов // Вестник МГТУ им. Н.Э. Баумана. Серия «Естественные науки». – 2012. – № 6. – C. 101-113. Димитриенко Ю.И. Многомасштабное моделирование упругих композиционных материалов / Ю.И. Димитриенко, А.П. Соколов // Математическое моделирование. – 2012. – Т. 24, №5. – С. 3-20. Димитриенко Ю.И. Об упругих свойствах композиционных материалов / Ю.И. Димитриенко, А.П. Соколов // Математическое моделирование. – 2009. – Т. 21, №4. – С. 96-110. Лапин А.А. Плоская деформация резинокордовой ткани / А.А. Лапин // Расчеты на прочность в машиностроении. – М.: Машгиз, 1955. – С. 87-99. Карнаухов В.Г. Влияние деформаций сдвига на эффективность работы пьезоактуаторов при активном демпфировании колебаний прямоугольной пластины / В.Г. Карнаухов, В.И. Козлов, Т.В. Карнаухова // Доповіді Національної академії наук України, № 2, 2015. – С. 50-54. Карнаухов В.Г. Вынужденные колебания анизотропной прямоугольной пластины с пьезосенсорами при учете сдвиговых деформаций / В.Г. Карнаухов, В.И. Козлов, Т.В. Карнаухова // Доповiдi Нацiональної академiї наук України, № 3. – 2015. – С. 45-49. Класторны М. Точная теория жесткости однонаправленных волокнисто-армированных композитов / М. Класторны, П. Кондерла, Р. Пиекарский // Механика композитных материалов. – 2009. – Т. 45, № 1. – С. 109-144. Композиционные материалы: Справочник / [В.В. Васильев, В.Д. Протасов, В.В. Болотин и др.]; Под общ. ред. В.В. Васильева, Ю.М. Тарнопольского. – М.: Машиностроение, 1990. – 512 с. Композиционные материалы: Справочник / Под ред. Д.М. Карпиноса. – К.: Наукова думка, 1985. – 592 с. Конструктивно-технологическое решение и несущая способность межступенного отсека ракеты-носителя «Циклон-4» из полимерных композиционных материалов / А.М. Зиновьев, А.П. Кушнарев, А.В. Кондратьев [и др.] // Авиационно-космическая техника и технология. – 2013. – № 33(100). – С. 46-52. Королев В.И. Слоистые анизотропные пластинки и оболочки из армированных пластмасс / В.И. Королев. – М.: Машиностроение, 1965. – 272 с. Марчук А.В. Применение полуаналитического метода конечных элементов для решения задач устойчивости слоистых конструкций с отслоениями / А.В. Марчук, В.Г. Пискунов // Механика композиционных материалов и конструкций. – 1998. – Т.4. – № 3. – С. 3-9. Математическое моделирование в нелинейной механике (Обзор программных комплексов для решения задач моделирования сложных систем) / Е.Н. Чумаченко, Т.В. Полякова, А.С. Аксенов [и др.] // Пр-2155, Институт космических исследований РАН. – М., 2009. – 43 с. Немировский Ю.В. Прочность элементов конструкций из композитных материалов / Ю.В. Немировский, Б.С. Резников. – Новосибирск: Наука, 1986. – 166 с. Портной К. И., Салибеков С. Е., Светлов И. Л., Чубаров В. М. Структура и свойства композиционных матереалов. Москва: Машиностроение, 1979. 225 с. Расчет неоднородных пологих оболочек и пластин методом конечных элементов / [В.Г. Пискунов, В.Е. Вериженко, В.К. Присяжнюк и др.]. – К.: Вища школа, 1987. – 200 с. Рогов В. А. Конструкционные и функциональные материалы современного машиностроения. Москва : Масштаб, 2006. 736 с. Рябов А.Ф. К теории многослойных пластин несимметричной структуры с ортотропными слоями / А.Ф. Рябов, А.О. Рассказов // Прикл. механика. – 1974. – Т. 10, вып. 2. – С. 62-68. Сметанкіна Н.В. Моделювання коливань шаруватих циліндричних оболонок складної форми при ударному навантаженні / Н.В. Сметанкіна / Вісник Запорізького національного університету. Фізико-математичні науки, № 1, 2015. – С. 162-170. Терегулов А.Г. К теории многослойных анизотропных оболочек / А.Г. Терегулов // Исследования по теории пластин и оболочек. – Казань: Казан. ун-т, 1970. – Вып. 6-7. – С. 762-767. Фомичев Ю.И. Напряженно-деформированное состояние многослойных ортотропных оболочечных конструкций в проблеме расчета резинокордных композитов и шин / Ю.И. Фомичев // Труды восьмого симпозиума «Проблемы шин и резинокордных композитов. Дорога, шина, автомобиль». – М.: НИИШП. – 1997. – Т. 2. – С. 418-423. Черепанов Г.П. Механика разрушения композиционных материалов / Г.П. Черепанов. – М.: Главная редакция физико-математической литературы издательства «Наука», 1983. – 296 с. Barbero E.J. Finite Element Analysis of Composite Materials (Composite Materials: Design and Analysis) / E.J. Barbero. – Boca Raton: CRC Press, 2007. – 360 p. Concise encyclopedia of composite materials / edited by A. Kelly. – Cambridge: MIT Press, 1989. – 317 p. Dvorak G. Micromechanics of Composite Materials / G. Dvorak. – New York-London: Springer, 2013. – 442 p. Gopalakrishnan S. Spectral Finite Element Method: Wave Propagation, Diagnostics and Control in Anisotropic and Inhomogenous Structures / S. Gopalakrishnan, A. Chakraborty, D.R. Mahapatra. – London: Springer, 2008. – 440 p. Finite element modelling of composite materials and structures / [F.L. Matthews, G.A.O. Davies, D. Hitchings, C. Soutis]. – Cambridge: Woodhead Publishing, 2000. – 214 p. Kwon Y.W. Multiscale Modeling and Simulation of Composite Materials and Structures / Y.W. Kwon, D.H. Allen, R. Talreja. – New York: Springer, 2007. – 630 p. Mukhopadhyay М. Mechanics of Composite Materials and Structures / М. Mukhopadhyay. – Hyderabad: Universities Press, 2005. – 371 p. Ochoa O.O. Finite Element Analysis of Composite Laminates / O.O. Ochoa, J.N. Reddy. – Dordrecht: Kluwer academic publishers, 1992. – 206 p. Soares C.A.M. Mechanics of composite materials and structures / C.A.M. Soares, C.M.M. Soares, M.J.M. Freitas. – Dordrecht: Kluwer academic publishers, 1999. – 517 p. Tang T. A variational asymptotic micromechanics model for predicting conductivities of composite materials / T. Tang, W. Yu // Journal of mechanics of materials and structures. – 2007. – Vol. 2, N 9. – P. 1813-1830. Tang T. Variational Asymptotic Micromechanics Modeling of Composite Materials / T. Tang. – Logan: Utah State University, 2008. – 280 p. Tenek L.T. Finite Element Analysis for Composite Structures / L.T. Tenek, J. Argyris. – Dordrecht: Kluwer academic publishers, 1997. – 339 p. Yu W. A variational asymptotic micromechanics model for predicting thermoelastic properties of heterogeneous materials / W. Yu, T. Tang // International Journal of Solids and Structures. – 2007. – Vol. 44. – P. 7510-7525. Yu W. Variational asymptotic method for unit cell homogenization / W. Yu, T. Tang // Advance s in Mathematical Modeling and Experimental Methods for Materials and Structures. – New York: Springer, 2010. – P. 116-130. Zhong W. A computer simulation of single fiber pull out process in a composite / W. Zhong, N. Pan // Journal of Composite Materials. – 2003. – Vol. 37, № 21. – P. 1951-1969. |
