Отчет. Курсовая работа ар по дисциплине Основы управления техническими системами
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (национальный исследовательский университет) Факультет радиоэлектроники летательных аппаратов Кафедра 404 «Конструирование, технология и производство радиоэлектронных средств» КУРСОВАЯ РАБОТААР по дисциплине «Основы управления техническими системами»
Дата сдачи: «____»_____________2021 г. Дата защиты: «____»_____________2021 г. Оценка: _________________ Москва 2021 ОглавлениеЗадание 2 1 Анализ задания 4 2 Анализ устойчивости по критерию Рауса – Гурвица 4 4 Анализ ошибок в системе 7 8 Анализ управляемости модели объекта 15 13 Разработка аналоговой схемы оптимальной САУ 19 ЗаданиеВариант №38 Динамическая система представлена передаточной функцией: 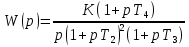 Параметры системы: К=20, Т1=16с, Т2=5с, Т3=0.25с, Т4=0.1с Провести предварительный анализ ПФ: состав, астатизм, априорные значения коэффициентов ошибок. Оценить устойчивость по критерию Гурвица. В случае неустойчивости, найти критическое значение коэффициента передачи (усиления) Ккр. Принять К=0.5 Ккр и вновь оценить устойчивость. Оценить устойчивость по критерию Михайлова с новым значением К, схематично изобразить годограф с указанием координат точек пересечения с осями. Определить коэффициенты ошибок по положению, скорости и ускорению, вычислить установившуюся ошибку при входном сигнале x(t) = 2 + 1.5t + 0.5t2. Рассчитать передаточную функцию последовательного корректирующего устройства по дополнительно выданному заданию*. Проверить расчёты, занести данные в таблицу. Разработать математическую модель системы в пространстве состояний двумя способами (формальным и декомпозиции). Привести в записке расчеты, эквивалентную схему, соответствующие системы уравнений и матрицы коэффициентов. Подтвердить правильность разработанных моделей путем сравнения переходных процессов по выходным переменным. Привести в записке таблицы моделирования для выходной переменной. Далее используется модель декомпозиции. Выполнить на ЭВМ анализ управляемости. Рассчитать оптимальный детерминированный регулятор по заданному критерию. Выполнить моделирование полученной САУ в режиме отработки ненулевых начальных условий. Построить график переходного процесса, определить доступные параметры переходного процесса. Рассчитать матрицу усиления оценивателя. Записать уравнения оценивателя в развернутой форме и соответствующие матрицы. Выполнить моделирование оценивателя, построить график переходного процесса, определить доступные параметры. Разработать аналоговую схему оптимальной САУ, указав на схеме фактические значения заданных и рассчитанных параметров. Заданную часть САУ на схеме представить блоком «объект управления». 1 Анализ заданияДля выполнения предварительного анализа опишем состав передаточной функции (ПФ). Исходя из задания, имеем: Одно интегрирующее звено 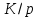 Одно форсирующее звено 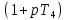 Три инерционных звена 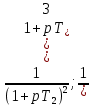 Подставляя численные значения: 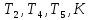 – в передаточную функцию, получаем: – в передаточную функцию, получаем: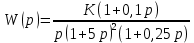 Вычисляем сопряженные частоты: 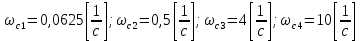 2 Анализ устойчивости по критерию Рауса – ГурвицаВ критерии Рауса – Гурвица рассматривается характеристический полином замкнутой системы А(р). 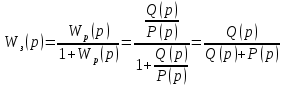 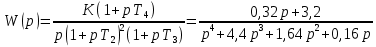 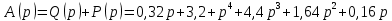 После несложных преобразований имеем: 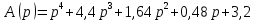 По этому полиному можно составить матрицу Гурвица: 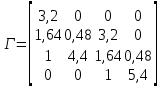 Определители матрицы: |Г1|=4,4 >0 |Г2|=6,736 >0 |Г3|=-58,71872 <0 |Г4|=4×|Г3| <0 Вывод – система неустойчивая. Определим 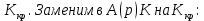 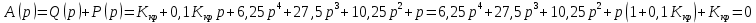 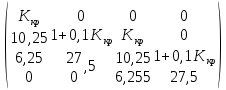 |Г3|=275,625-729,3125p-0,0625 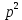 =0 =0 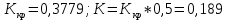 3 Анализ устойчивости по критерию Михайлова Критерий Михайлова основан на анализе годографа характеристического полинома замкнутой системы. С этой целью аргумент р заменяется на 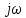 и полином разделяется на вещественную и полином разделяется на вещественную 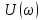 и мнимую и мнимую 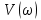 части. Далее строится годограф в декартовой системе координат, причем нет необходимости в детальном воспроизведении этой кривой. Достаточно указать точки ее пересечения с осями координат. части. Далее строится годограф в декартовой системе координат, причем нет необходимости в детальном воспроизведении этой кривой. Достаточно указать точки ее пересечения с осями координат.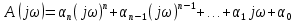 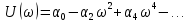 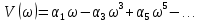 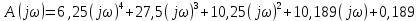 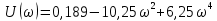 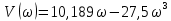 Вычислим координаты точек пересечения годографа с осями координат, которые занесем в таблицу1. Таблица 1 – Точки пересечения годографа с осями координат
На основании данных таблицы строится кривая (без соблюдения фактического масштаба), показанная на рисунке 1. Вывод относительно устойчивости замкнутой системы делается с учетом скорости перемещения точки на годографе по осям координат в 4-м квадранте. Из формул видно, что по вещественной оси изменение координаты точки происходит в четвёртой степени, а по мнимой оси – в третьей. Это позволяет сделать вывод, что в бесконечности кривая сколь угодно близко подходит к вещественной оси, не пересекая её. Таким образом, годограф охватывает 4 квадранта и система устойчива. 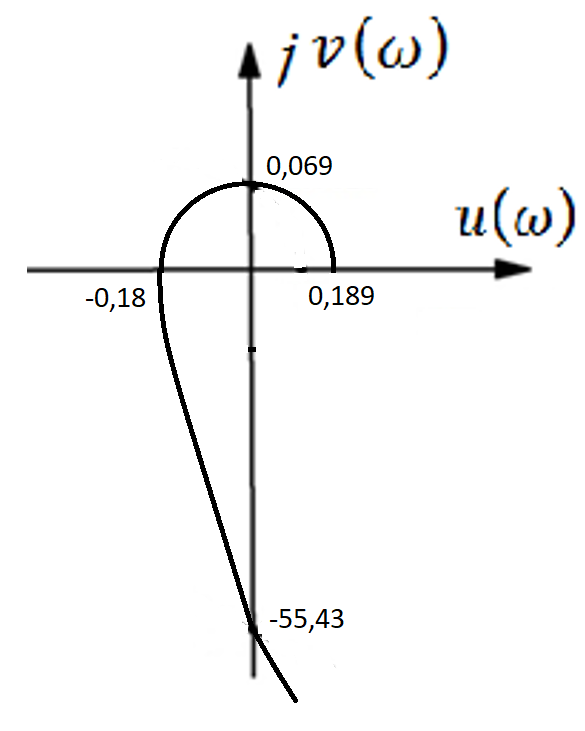 Рисунок 1 – Годограф Михайлова 4 Анализ ошибок в системеПередаточная функция ошибки S(p) определяется как отношение изображений по Лапласу ошибки к входному сигналу: 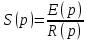 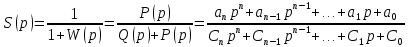 Подстановка характеристических полиномов разомкнутой и замкнутой систем даёт: 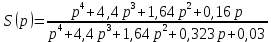 Следуя принятым обозначениям коэффициенты ошибок выражаются следующим образом: 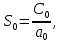 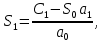 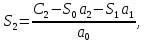 где: где: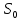 – коэффициент ошибки по положению, – коэффициент ошибки по положению,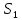 – коэффициент ошибки по скорости, – коэффициент ошибки по скорости,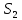 – коэффициент ошибки по ускорению. – коэффициент ошибки по ускорению.В результате получаем следующие значения: 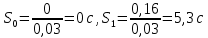 , ,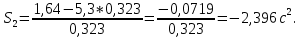 Установившейся называется ошибка, которая остаётся после завершения всех переходных процессов в системе и рассчитывается для определенного детерминированного входного сигнала. В задании указан задающий входной сигнал r(t)=2+1,5t+0,5 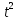 , имеющий все три составляющие движения: начальное положение, скорость и ускорение. Расчет установившейся ошибки выполняется по формуле, являющейся результатом предельного перехода при t→ , имеющий все три составляющие движения: начальное положение, скорость и ускорение. Расчет установившейся ошибки выполняется по формуле, являющейся результатом предельного перехода при t→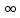 . .e0 = S0x(t)│t=0 + S1ẋ(t) │t=0 + S2ẍ(t) │t=0 , где х(t)- входной сигнал. Для нашего случая получим e0 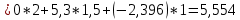 . .Результат нельзя считать удовлетворительным, поскольку присутствует значительная составляющая ошибки по положению. Чтобы улучшить потенциальные характеристики САУ, попытаемся использовать последовательную коррекцию. 5 Расчет передаточной функции устройства последовательной коррекции Задача проектирования обычно решается в два этапа. На первом этапе анализируется передаточная функция разомкнутой исходной системы и возможность реализации характеристик будущей САУ. На втором этапе производится расчет параметров желаемой передаточной функции и определение ПФ последовательного корректирующего устройства WK(p). Набор дополнительных параметров, обеспечение которых требуется по техническому регламенту:
Сравнение заданных здесь коэффициентов ошибок с полученными в результате анализа свидетельствует о невозможности получения нужных величин, создавая САУ на исходной передаточной функции. Поэтому выполняется расчет «желаемой» передаточной функции, обеспечивающей поставленную задачу. Практикой проектирования следящих систем установлено, что в качестве передаточной функции желаемой системы, удовлетворяющей поставленным требованиям, следует выбрать выражение 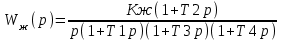 . .Здесь знаменатель включает в себя инерционное звено из исходной системы, имеющее постоянную времени меньше рассчитанной желаемой T3. Если оно обнаружится, то мы включаем его в состав Wж(р) и переобозначаем его постоянную времени как Т4. По заданным техническим требованиям к проектируемой системе определяем: 1. Коэффициент усиления желаемой ПФ 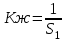 . .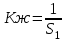 = = 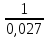 = 37,037 = 37,0372. Сопряженные частоты 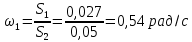 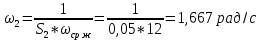 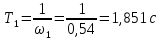 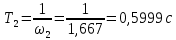 3. Сопряженная частота ω3 (и Т3) рассчитываются из запаса устойчивости по фазе 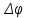 . .Δφ = 90о 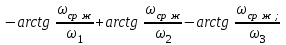 . .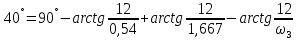 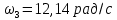 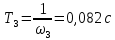 Заметим, что без «прибавки» 7о мы прогнозируем отсутствие в исходной ПФ звена, имеющего постоянную времени меньше рассчитанной желаемой T3 = 0,082 с. Так как при сравнении исходные значения больше T3, то желаемая функция приобретает следующий вид. 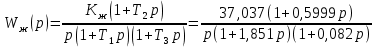 Далее, из выражения Wж(p)=Wи(p)*Wк(p) можно найти 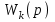 . Записываем отношение Wк(p)=Wж(p)/Wи(p) и сокращаем всё, что сокращается. Выписываем отдельно Wк(p). . Записываем отношение Wк(p)=Wж(p)/Wи(p) и сокращаем всё, что сокращается. Выписываем отдельно Wк(p).Не подлежит сомнению, что Wж(p) и 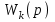 приводятся как в символьном, так и в числовом выражении. приводятся как в символьном, так и в числовом выражении.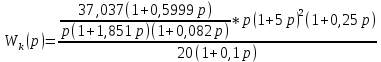 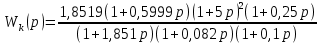 Полученная ПФ корректирующего устройства достаточно сложна для технической реализации и, вероятно, будет создавать дополнительные помехи и нестабильности в работе САУ. Поэтому обратимся к методам создания систем оптимального управления. Наиболее рациональным с инженерной точки зрения является метод Понтрягина с матричным уравнением Риккати. Для этого вначале необходимо разработать описание объекта управления в виде дифференциальных уравнений состояния. 6 Получение описания в переменных состояния 6.1 Формальный метод Представим матрицы модели в переменных состояния, полученной формальным методом. 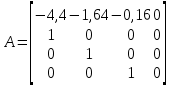 - матрица объекта - матрица объекта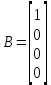 - матрица управления - матрица управления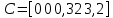 - матрица выхода - матрица выходаЗапишем уравнения состояния: 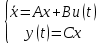 , где , где 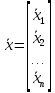 и и 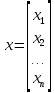 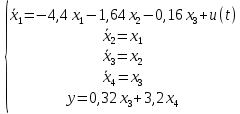 Уравнения в таком формате не всегда удобны для использования в автоматизированных системах проектирования из-за сильной разреженности матриц. Другим подходящим методом является метод декомпозиции. 6.2 Метод декомпозиции По заданной передаточной функции составляется рациональная последовательность «композиций» 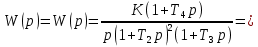 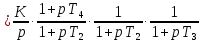 На основании базовых фрагментов строится эквивалентная схема:     1 . . .           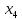 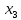 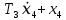 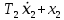 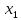 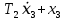 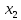 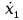 . 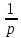      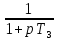 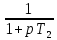 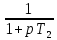 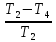 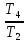 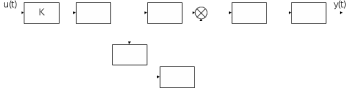 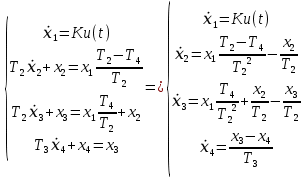 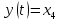 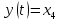 После необходимых преобразований получается система уравнений состояния в канонической форме: 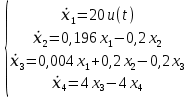 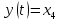 Запишем также матрицы коэффициентов векторно-матричной формы, необходимые для подстановки в программы проектирования: 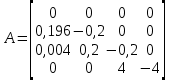 ; ; 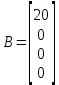 ; ; 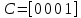 ; ;Для проверки правильности разработанных моделей выполняется моделирование при одинаковых условиях. Идентичность выходных переменных обеих моделей будет свидетельствовать о их правильности. Результаты моделирования представлены в таблице 2. Таблица 2 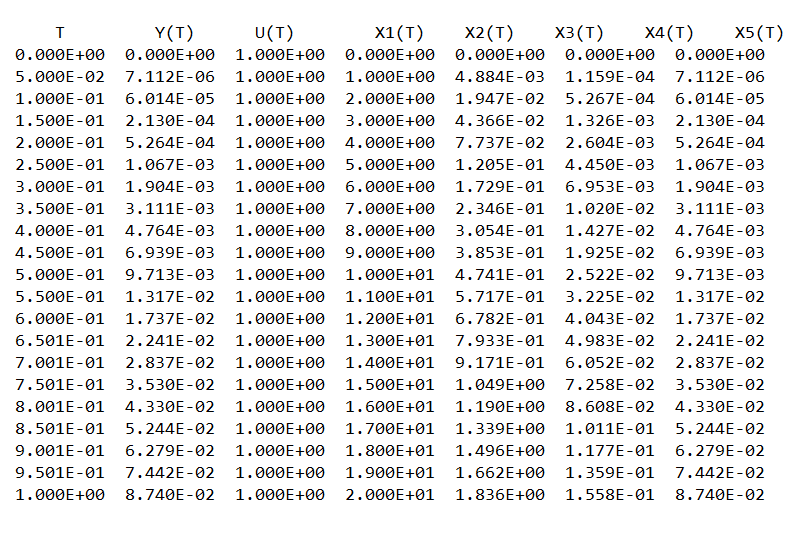 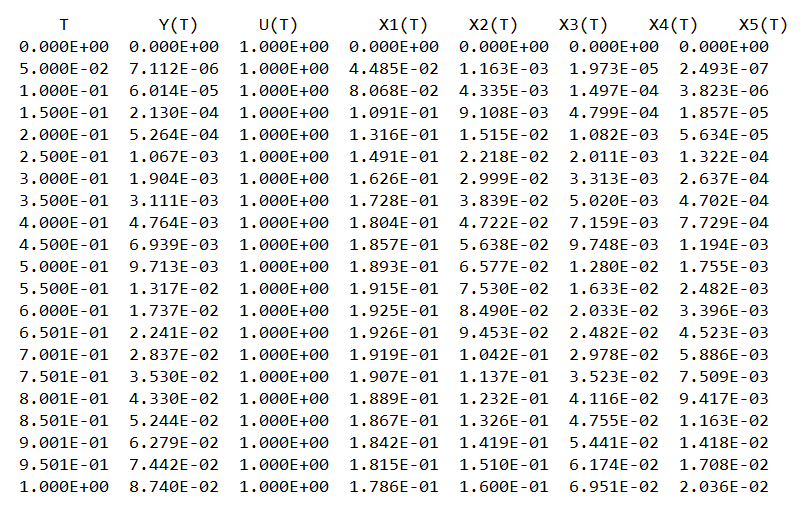 Результаты совпадают, следовательно, модели составлены правильно. 7 Формирование критерия качества Матричное уравнение Риккати предполагает использование квадратичной меры ошибки вида H = xTQx + uTLu. В данном варианте с матрицей С=[0 0 0 1] рекомендовано использовать весовую матрицу Q вида: 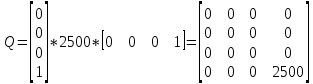 При этом L=1. Таким образом, критерий качества 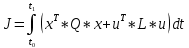 в скалярной форме запишется следующим образом 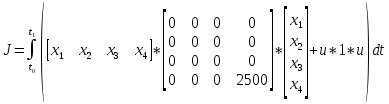 = 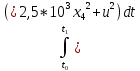 Теперь можно перейти к следующему этапу проектирования – расчету детерминированной оптимальной системы управления. 8 Анализ управляемости модели объектаАнализ управляемости предшествует процедуре расчета оптимального регулятора. Для этой цели используется специальная программа. 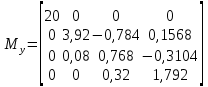 Вывод: Объект управляем. Ранг матрицы управляемости равен 4. 9 Расчет и моделирование оптимального регулятора Коэффициенты усиления регулятора: g11 = 16,67; g12 = 0,001796; g13 = 3,675* 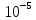 ; g14 = 5,368* ; g14 = 5,368*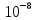 ; ; Следовательно, уравнение оптимального детерминированного управления: 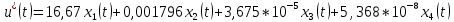 Результаты моделирования представлены в таблице 3 Таблица 3
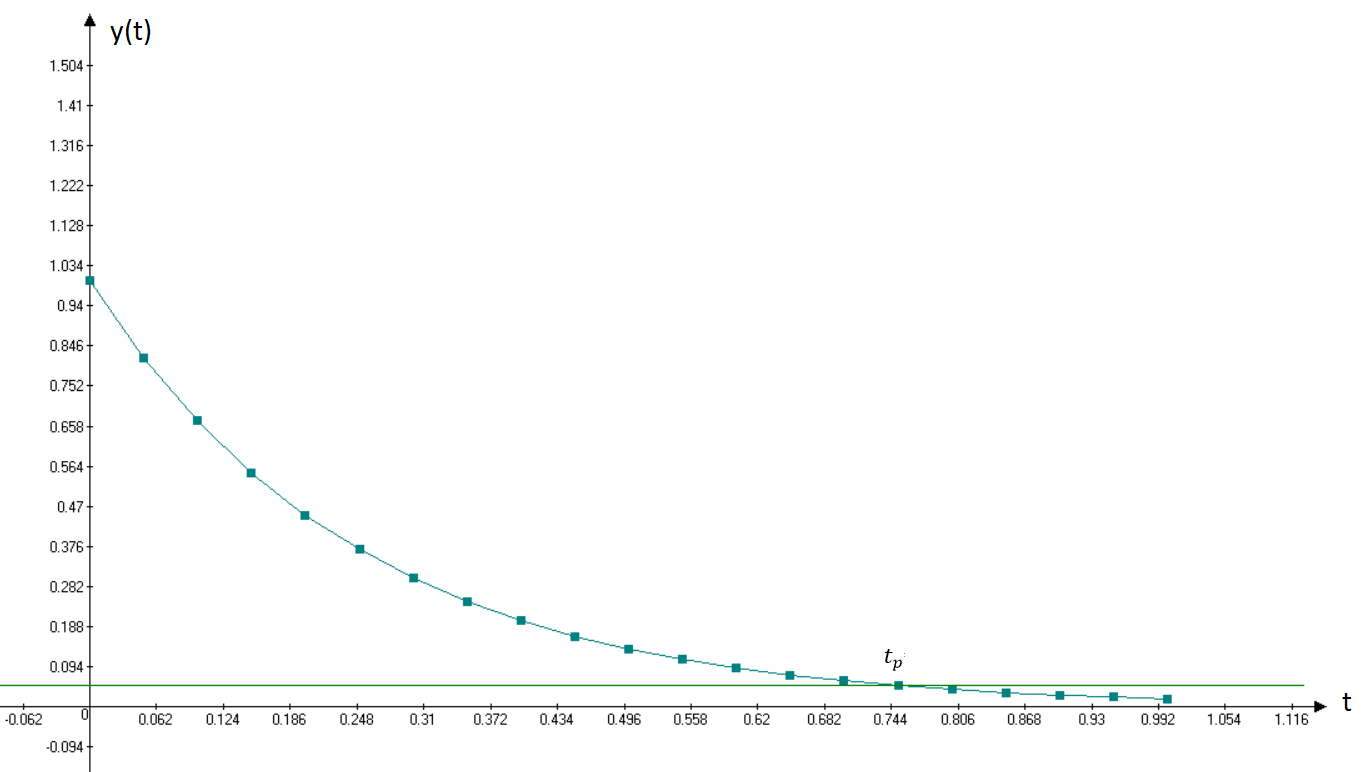 Рисунок 2 – График моделирования регулятора Время регулирования tр = 0.7491с 10 Анализ наблюдаемости модели объекта управления Для анализа наблюдаемости воспользуемся программой sapr2. На выходе получаем матрицу наблюдаемости. Вывод: Объект наблюдаем. Ранг матрицы наблюдаемости равен 4. 11 Расчет матрицы усиления оценивателя Для расчета коэффициентов усиления воспользуемся программой fil64. В результате получаем матрицу коэффициентов усиления фильтра Калмана: K = 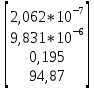 12 Моделирование оценивателя Для моделирования оценивателя воспользуемся программой simul. При вводе данных в качестве матрицы А записываем матрицу А-КС, а в качестве матрицы B матрицу K.  Результаты моделирования приведены в таблице 4, а график, построенный по данным таблицы, представлен на рисунке 3. Результаты моделирования приведены в таблице 4, а график, построенный по данным таблицы, представлен на рисунке 3.Таблица 4 – Результаты моделирования 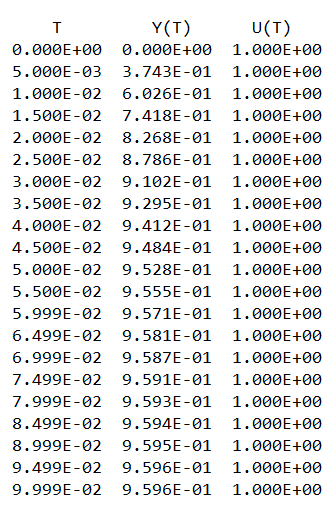 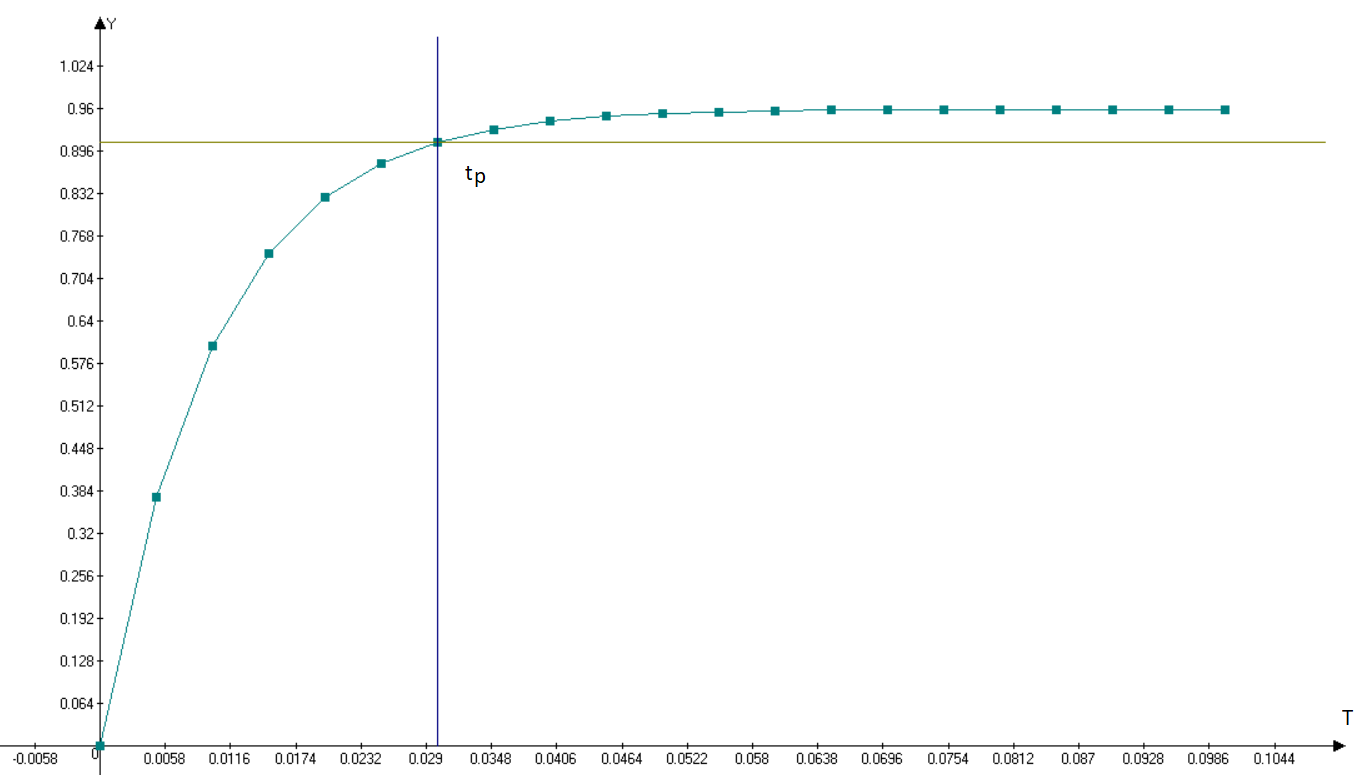 Рисунок 3 – График переходного процесса в оценивателе Время регулирования tр = 0.03 с. 13 Разработка аналоговой схемы оптимальной САУ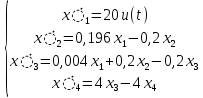 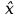 = =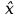 [A-KC]+Bu(t)+K(t)y(t); y(t)= [A-KC]+Bu(t)+K(t)y(t); y(t)=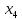 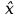 = =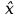 [A-KC]+Bu(t)+K(t) [A-KC]+Bu(t)+K(t)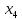 (t); (t);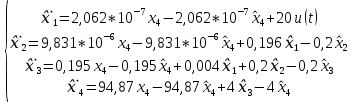 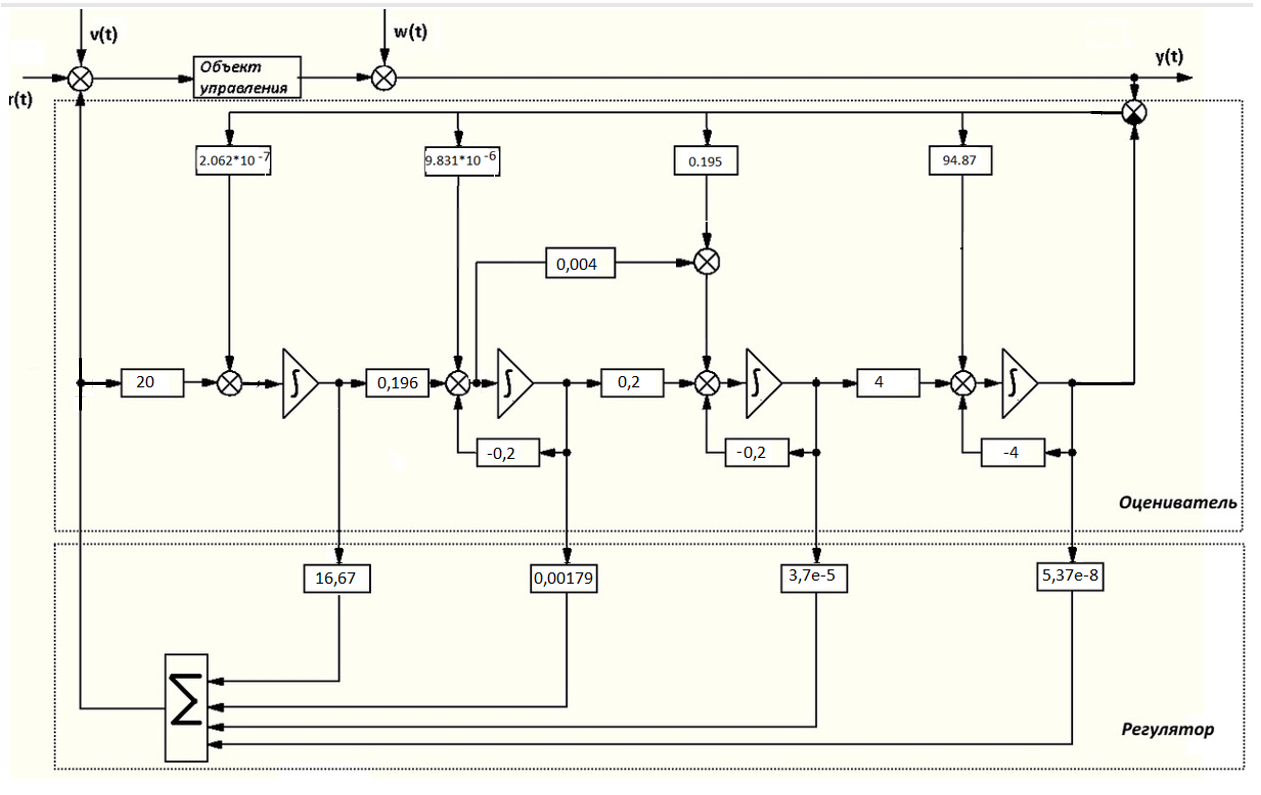 Рисунок 4 – Аналоговая схема оптимальной САУ Выводы В ходе работы выполнен расчет САУ по классической схеме и проектирование оптимальной системы управления. Анализ передаточной функции «заданной части» выявил потенциальные возможности классической схемы САУ. Анализ устойчивости по критерию Рауса-Гурвица показал неустойчивость замкнутой системы и позволил скорректировать коэффициент передачи с целью обеспечения устойчивости. Далее устойчивость скорректированной системы подтверждена с помощью критерия Михайлова. Вычислены коэффициенты ошибок по положению, скорости и ускорению, а также была рассчитана установившаяся ошибка при заданном входном сигнале. Выполнен расчет передаточной функции последовательного корректирующего устройства и даны рекомендации по его технической реализации. Во второй части работы выполнен расчет и моделирование оптимальной системы управления, включающей регулятор и оцениватель. Установлены и подтверждены управляемость и наблюдаемость объекта. Таким образом, достигнуты следующие результаты проектирования: Коэффициенты ошибок: S0=0 c; S1=5,3 c; S2=-2,396 c2 Установившаяся ошибка на заданном входном сигнале: е0=5,554 Время регулирования детерминированной САУ с обратной связью по состоянию tp=0.7491 c. Время регулирования оценивателя состояния tроц=0.03 с; Переходный процесс в регуляторе и оценивателе экспоненциальный. Время регулирования оценивателя существенно меньше регулируемой САУ, следовательно, оцениватель может быть использован в системе управления. |

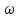
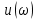
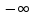
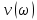
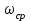 ж , , рад/с
ж , , рад/с