Курсовая работа химическая термодинамика Выполнила студентка группы х41(2) Кямякова Галия Ибрагимовна Пенза 2008 г
 Скачать 63.37 Kb. Скачать 63.37 Kb.
|
|
Федеральное агентство по образованию Пензенский государственный педагогический университет им. В.Г. Белинского КУРСОВАЯ РАБОТА Химическая термодинамика Выполнила студентка группы Х-41(2): Кямякова Галия Ибрагимовна Пенза 2008 г. Содержание Введение Глава 1. Первый закон термодинамики 1.1 Вопросы и задания 1.2 Примеры 1.3 Задачи Глава 2. Приложение первого закона термодинамики к химии. Термохимия 2.1 Вопросы и задания 2.2 Примеры 2.3 Задачи Глава 3. Второй закон термодинамики. Энтропия 3.1 Вопросы и задания 3.2 Примеры 3.3 Задачи Глава 4. Термодинамические потенциалы 4.1 Примеры 4.2 Задачи Литература Введение Физическая химия – наука, которая изучает общие закономерности физических процессов и является теоретической основой всей химической науки и технологии химических производств. Наиболее важным и в то же время одним из самых сложных разделов физической химии является химическая термодинамика. В данной курсовой работе приведен перечень вопросов и задач по химической термодинамике. Эти задачи носят комплексный характер и позволяют ученикам подготовиться к химическим олимпиадам. Целью настоящей работы явился подбор заданий по химической термодинамике, адаптация их к требованиям химических олимпиад для школьников, а так же разработка методики их решения с учетом межпредметных связей с математикой и физикой. Решение задач дает возможность применить теоретические знания на практике, расширить, углубить и систематизировать их, стимулируют мыслительную деятельность учеников, развивают последовательность в действиях, логику. Глава 1. Первый закон термодинамики Вопросы и упражнения Что такое термодинамика и какие явления она изучает? Приведите несколько формулировок первого закона термодинамики и покажите, что они не противоречат друг другу. Почему первый закон термодинамики называют первым началом? Что такое система? Какие ее виды различают? Дайте определение и приведите примеры термодинамических процессов: изотермического, изобарического, изохорического и адиабатического. Что такое внутренняя энергия системы и из чего она слагается? Дайте определение идеального газа. Что собой представляет внутренняя энергия идеального газа? Почему термодинамика рассматривает не абсолютное значение внутренней энергии, а только ее изменение? Что такое энтальпия и какова ее связь с внутренней энергией? Почему для конденсированных систем разница между энтальпией и внутренней энергией мала, а для систем газообразных значительна? Перечислите способы передачи энергии от одной системы к другой. Что такое теплота и работа? Дайте определение теплоемкости удельной, атомной, молярной (мольной)? Какая связь существует между мольными теплоемкостями при постоянном давлении и постоянном объеме? Работа определяется двумя величинами: фактором интенсивности и фактором емкости (экстенсивности). Что будут представлять собой эти факторы при совершении механической работы, электрической и работы по расширению газов? Что такое максимальная работа расширения идеального газа? Почему газ, расширяясь в вакууме, работы не совершает? Напишите уравнения, выражающие максимальную работу расширения идеального газа при изотермическом, изобарическом, изохорическом и адиабатическом процессах. Дайте определение обратимым и необратимым термодинамическим процессам. Приведите примеры. Можно ли реальные природные процессы считать полностью обратимыми? 1.2 Примеры Пример 1-1 Газ расширяясь от 10 до 16 л при постоянном давлении 101,3103 н/м2, поглощает 126 Дж теплоты. Определите изменение внутренней энергии газа. Решение: p1 = p2 = 101,3103 Па, V1 = 10 л = 1*10-2 м3 , V2 =16 л = 1610-3 м3, Qp = 126 Дж. Согласно первому закону термодинамики U = Qp – W. Работа, совершенная газом при изобарическом расширении, может быть вычислена по уравнению W= p (V2–V1); Отсюда U = Qp - p (V2–V1); U = 126 - 101,3103 (1* 10-2 – 1610-3) = 481,8Дж Ответ: 481,8Дж Пример 1-2Рассчитайте работу изотермического (27С) расширения 1 моль углекислого газа от 2,24 до 22,4 л. Решение: n = 1 моль, V1 = 2,24л = 2,2410-3 м3 , V2 = 22,410-3 м3 , Т = 27С = 300 K. Работа изотермического расширения системы может быть вычислена по уравнению: W = nRT 2,3 lg(V2 /V1); W = 18,3143002,3 lg (22,410-3 / 2,2410-3) = 5736,66 Дж Ответ: 5736,66 Дж Пример 1-3При 273 К и 1,0133105 Па нагревают 510-3 м3 криптона до873 К при постоянном объеме. Определите конечное давление газа и теплоту, затраченную на нагревание. Решение: V = 510-3 м3, T1 = 273 К, Т2 = 873 К, р1 = 1,0133105 Па. Теплоту, затраченную на нагревание можно найти по формуле: Qv = nCv(T2 – T1). Количество криптона вычисляется из уравнения состояния идеального газа: pV = nRT; n = p1V/RT1; n = 1,0133105 510-3 /8,314273 = 0,223 моль. Для одноатомных газов Сv = 3/2R ; Qv = 0,2233/28,314(873 – 273) = 1668,620 Дж Конечное давление при постоянном объеме и известной температуре можно найти по закону Шарля: p1/T1 = p2/T2; p2 = p1T2/ T1; p2 = 1,0133105873/273 = 3,2403105 Па Ответ: Qv = 1668,620 Дж, p2= 3,2403105 Па Пример 1-4 Один моль одноатомного газа, взятого при 25С и давлении 1,013105 Па, адиабатически расширился до 0,05 м3. Каковы будут конечные давление и температура? Решение: T1 = 25С = 298 K, P1 = 1,013105 Па, V2 = 0,05 м3. Исходный объем газа (n = 1): V1 = nRT1/р1 = 18,314298/1,013105 = 2,44510-2 м3. Конечные давление и температуру можно найти из уравнения адиабаты ( = Ср/Сv для одноатомных газов близко к 5/3): р1V15/3 = р2V25/3, р2 = р1(V1/ V2 )5/3, р2 = 1,013105(2,44510-2/5,00010-2)5/3 Па = 0,3105 Па Т1V1-1 = Т2V2-1, Т2 = Т1 (V1/ V2)-1, Т2 = 298(2,44510-2/5,00010-2)5/3 – 1К = 183 К Ответ: р2 =0,3105 Па, Т2 = 183 К. 1.3 Задачи Путем нагревания при постоянном давлении в 1,013105 Па газу сообщено 2093, 4 Дж теплоты. Определите работу, совершенную газом, и изменение внутренней энергии данного газа, если он при этом расширился от 1 до 2 л. Один моль дифторметана (идеальный газ), взятый при 0С и 1 атм, нагрет при постоянном давлении до утроения объема. Рассчитайте изменение энтальпии и внутренней энергии в этом процессе, если зависимость теплоемкость дифторметана от температуры имеет вид: Ср = 20,26 + 7,5910-2Т(Дж моль-1К-1) (∆H = 33,7 кДж; ∆U = 29,1 кДж) Определите изменение внутренней энергии при изобарическом (1,013105 н/м2) испарении 100 г воды при 150С, если объемом жидкой воды пренебречь. Теплота испарения воды при 150С равна 2112,66 Дж/г. Азот (5 моль) при 100С занимал объем 0,025 м3. При нагревании газа до 200С было затрачено 14650 Дж. Определите Ср и конечный объем, если давление газа при этом не изменилось. Определите работу, совершаемую азотом при изотермическом (20С) расширении его от 0, 015 до 0,1 м3, если начальное давление составляло 3,039105 Па. Каково будет конечное давление? (W = 657 Дж, р2 = 45600 н/м2) При 298 К одноатомный газ в идеальном состоянии изотермически и обратимо расширяется от 1,5103м3 до 10103 м3, при этом поглощается 966103 Дж теплоты. Рассчитайте число молей газа, участвующего в процессе.(205,51) Один моль идеального газа, взятого при 25С и 100 атм, расширяется обратимо и изотермически до 5 атм. Рассчитайте работу, поглощенную теплоту, изменение внутренней энергии и энтальпии в этом процессе. Сколько нужно затратить теплоты, чтобы изохорически нагреть 25 г кислорода от 0 до 50С? (811,85 Дж) Какое количество теплоты необходимо для изохорического нагревания 50 г углекислого газа в интервале температур от 300 до 400С, если Cv = 40,2 Дж/моль? (4,56 кДж) В резервуаре вместимостью 510-2 м3 при 200 К и 0,5105 Па содержится азот. Определите теплоту, которую необходимо передать газу, чтобы его давление стало равным 2105 Па. Считать азот в указанных условиях идеальным газом. (18,7498 кДж) Один моль ксенона, находящийся при 25С и 2 атм, расширяется адиабатически: а) обратно до 1 атм, б) против давления 1 атм. Какой будет конечная температура в каждом случае? ( а)225 К, б)238 К) Определите работу адиабатического обратимого расширения 3 моль аргона от 0,05 до 0,50 м3. Начальная температура газа 298 К. (8,745105Дж) При 298 К 110-2 кг кислорода сжимается адиабатически от 810-3 до 510-3 м3. Определите конечную температуру, работу процесса сжатия, изменение внутренней энергии и изменение энтальпии, если Сv = 5/2R. (359, 637 К; -400,37 Дж; 400,34 Дж; 1,335 кДж) Один моль фтороуглерода расширяется обратимо и адиабатически вдвое по объему, при этом температура падает от 298,15 до 248,44К. Чему равно значение СV?(31,6 Дж*моль-1*К-1) Глава 2. Приложение первого закона термодинамики к химии. Термохимия 2.1 Вопросы и задания Что называется тепловым эффектом химической реакции? Сформулируйте закон Гесса и следствия, вытекающие из него. Каково значение данного закона? Объясните, почему закон Гесса есть частный случай первого закона термодинамики? Применяя математическое выражение первого закона термодинамики, покажите, что тепловой эффект при постоянном давлении есть изменение энтальпии, а тепловой эффект при постоянном объеме – изменение внутренней энергии химической реакции. Какие химические реакции называются экзотермическими и эндотермическими? Приведите примеры. Почему для конденсированных систем разница между изменением энтропии и изменением внутренней энергии мала, а для газообразных значительна? Напишите уравнение, выражающее связь между тепловым эффектом при постоянном давлении и тепловым эффектом при постоянном объеме. Дайте определение понятиям: «теплота образования», «теплота разложения», «теплота растворения», «теплота сгорания», «теплота нейтрализации». Почему при определении теплот растворения на 1 моль различных растворенных веществ берется различное количество молей растворителя? Сформулируйте закономерности, установленные для теплот образования химических соединений. Чем объяснить постоянство теплот нейтрализации сильной кислоты сильным основанием? Одинаковый ли тепловой эффект будет при: а)нейтрализации серной кислоты едким натром, б) нейтрализации серной кислоты раствором аммиака? Дайте объяснение. Будет ли наблюдаться выделение или поглощение теплоты при сливании разбавленных растворов: а) хлорида калия и бромида натрия, б) хлорида калия и нитрата серебра, в) сульфата натрия и нитрата свинца, г) хлорида кальция и нитрата натрия? Как зависит тепловой эффект химической реакции от температуры? Напишите математическое выражение закона Кирхгофа. В каких случаях тепловой эффект химической реакции не зависит от температуры? Почему? 2.2 Примеры Пример 2-1Количество теплоты, выделенной при горении в стандартных условиях 2 г водорода в кислороде с образованием жидкой воды, равно 286 кДж. Чему равен тепловой эффект реакции при постоянном объеме? Решение: Находим количество водорода: n = m/М, n = 2/2 моль = 1 моль Записываем уравнение реакции: Н2(г) + 0,5О2(г) = Н2О(ж), Н = -286 кДж, Т = 298 К Тепловой эффект при постоянном объеме характеризуется изменением внутренней энергии (Qv = U). U в данной реакции можно рассчитать следующим образом: U = Н – рV = Н - nRT, U = -286103 -(-3)8,314298 Дж = 278567 Дж Ответ: 278,567103 кДж Пример 2-2Рассчитайте энтальпию образования сульфата цинка из простых веществ при Т = 298 К на основании следующих данных:ZnS = Zn + S, Н10 = 200,5 кДж моль-1,2ZnS + 3О2 = 2ZnO + 2SO2, Н20 = -893,5 кДж моль-1, 2SO2 + О2 = 2SO3, Н30 = -198,2 кДж моль-1, ZnSO4 = ZnO + SO3, Н40 = 235,0 кДж моль-1. Решение: Закон Гесса позволяет обращаться с термохимическими уравнениями как с алгебраическими Множитель ZnS = Zn + S, Н10=200,5 кДж моль-1 -12ZnS+3О2=2ZnO+2SO2, Н20=-893,5кДж моль-1 0,5 2SO2 + О2 = 2SO3, Н30=-198,2кДж моль-1 0,5 ZnSO4 = ZnO + SO3, Н40=235,0кДж моль-1 –1 Zn + S + ZnS + 1,5О2 + SO2 + 0,5О2 + ZnO + SO3 = ZnS + ZnO + + SO2 + SO3 + ZnSO4 Zn + S + 2О2 = ZnSO4 Нf0(ZnSO4) = -1Н10 + 0,5Н20 + 0,5Н30 - 1Н40, Нf0(ZnSO4)=-200,5+0,5(-893,5)+0,5(-198,2)–235,0 = = 981,35кДж моль-1 Ответ: 981,35 кДж моль-1 Пример 2-3 Пользуясь справочными данными, рассчитайте энтальпию реакции: 3Сu(ТВ)+8H(NO3)2(aq)=3Сu(NO3)2(aq)+2NO(г)+4H2O(ж) при 298 К. Решение: Сокращенное ионное уравнение реакции имеет вид: 3Cu(ТВ)+8H+(aq)+2NO3ˉ(aq)=3Сu2+(aq)+2NO(г)+4Н2О(ж), по закону Гесса, энтальпия реакции равна: rН0=4fН0(Н2О(ж))+2fН0(NO(г))+3fН0(Сu2+(aq))-2fН0(NO3ˉ(aq)) (энтальпии образования меди и иона Н+ равны, по определению, нулю). Подставляя значения энтальпии образования из справочника находим: rН0=(4(-285,8)+2·90,25+3·64,77–2(-205,0))кДж=-358,4кДж, (в расчете на три моля меди). Ответ: -358,4 кДж Пример 2-4 Рассчитайте энтальпию сгорания метана при 1000 К, если даны энтальпии образования при 298 К: fH(СН4) = -17,9 ккал/моль, fH(СО2) = -94,1 ккал/моль, fH(Н2О) = -57,8 ккал/моль. Теплоемкости газов (в калмоль-1К-1) в интервале от 298 до 1000 К равны: Ср(СН4)= 3,422 + 0,0178Т, Ср(О2) = 6,095 + 0,0033Т, Ср(СО2) = 6,369 +0,0102Т, Ср(Н2О(г)) =7,188 +0,0024Т Решение: Энтальпия реакции сгорания метана СН4(г) + 2О2(г) = СО2(г) + Н2О(г) при 298 К равна: rH298 = -94,1 + 2(-57,8) – (-17,9) = -191,8 ккал/моль. Найдем разность теплоемкостей как функцию температуры: Ср = Ср(СО2) + 2 Ср(Н2О(г)) - Ср(СН4) - 2Ср(О2), Ср = 5,16 – 0,0094Т (калмоль-1К-1). Энтальпию реакции при 1000 К рассчитаем по уравнению Кирхгофа: rH1000 = rH298 + 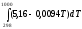 , , rH1000=(-191800+5,16(1000–298)–0,0094(10002– - 2982)/2) калмоль-1 = -192500 калмоль-1. Ответ: -192500 калмоль-1. 2.3 Задачи Определите тепловой эффект реакции: Al2Oкорунд + 3SO3 = Al2(SO4)3 кр +U, если реакция протекает при 298 К в автоклаве при постоянном объеме, а тепловой эффект реакции при р = const равен –573,4 кДж. (-566,0103кДж) Стандартная энтальпия реакции: СаСО3(тв) = СаО(тв) + СО2(г), протекающей в открытом сосуде при температуре 1000 К, равна 169 кДж моль-1. Чему равна теплота этой реакции, протекающей при той же температуре, но в закрытом сосуде? (160,7 кДжмоль-1) Рассчитайте энтальпию образования N2О5(г) приТ = 298 К на основании следующих данных:2 NО(г) + О2(г) = 2NО2(г), Н10 = -114,2 кДж моль-1,4NО2(г) + О2(г) = 2N2О5(г), Н20 = -110,2 кДж моль-1,N2(г) + О2(г) = 2NО(г), Н30 = 182,6 кДж моль-1.(13,3 кДжмоль-1) Реакция горения ацетилена при стандартных условиях выражается уравнением:С2Н2+2,5О2=2СО2+Н2Ож –1300кДж.Определите теплоту образования ацетилена при постоянном давлении (226,5 кДж).Стандартные энтальпии образования жидкой и газообразной воды при 298 К равны -285,8 и -241,8 кДж моль-1 соответственно. Рассчитайте энтальпию испарения воды при этой температуре. (44,0 кДж моль-1) Рассчитайте стандартный тепловой эффект реакции: CаSO4(ТВ) + Na2CO3(aq) = CaCO3(ТВ) + Na2CO3(aq) при 298 К, если fН0298 (CаSO4(ТВ)) = -1434 кДж моль-1(-5,0 кДж моль-1) Известны тепловые эффекты следующих реакций: СН3СООC2Н5(ж)+ОН¯(aq)=СН3СОО¯(aq)+C2Н5ОН(ж),rН0298=-54,7кДжмоль-1; Н3СООН(ж)+ОН¯(aq)=СН3СОО¯(aq)+Н2О(ж); rН0298=-57,3кДжмоль-1; СН3СООC2Н5(ж)+2Н2(г)=2C2Н5ОН(ж), rН0298=-76,4кДжмоль-1. Рассчитайте тепловой эффект реакции: C2Н5ОН(ж) + О2(г) = СН3СООН(ж) + Н2О(ж), если энтальпия образования жидкой воды равна -285,8 кДж моль-1.(-492,6 кДж моль-1) На сколько градусов повысится температура при растворении 0,5 моль серной кислоты в 400 г воды, если теплота растворения серной кислоты равна -74,94 кДж, а удельная теплоемкость раствора равна 3,77 Дж/г·град? (22,14С) Тепловой эффект растворения безводного сульфата лития равен –26,71 кДж моль-1. Тепловой эффект растворения кристаллогидрата Li2SO4H2O равен –14,31 кДж моль-1 при 298 К. Вычислите тепловой эффект образования Li2SO4H2O из безводной соли и воды. Определите процентное содержание воды в частично выветренном кристаллогидрате сульфата лития, если тепловой эффект растворения 1 кг этой соли равен –0,146103 кДж. (-12,40 кДж·моль-1) Рассчитайте изменение энтальпии при нагревании 2 кг -SiO2 от 298 до 800 К, если зависимость теплоемкости от температуры выражается уравнением: С0р = 46,94 +34,3110-3Т – 11,3105 /Т2. (1,0212·106 Дж) Зависимость теплового эффекта реакции Н2(г) + ½ О2(г) = Н2О(г) от температуры выражается уравнением: rHТ (Дж/моль) = -237,65103 – 13,01Т + 2,8810-3Т2 –1,71. Рассчитайте изменение теплоемкости Ср СV для этой реакции при 800 К. (Ср = -8,14 Дж моль-1К-1, СV = -3,98 Дж моль-1К-1) Определите тепловой эффект химической реакции СН3ОН(г) + 3/2О2 = СО2 + 2Н2О(г) при 500 К и стандартном давлении. При расчете воспользуйтесь средними теплоемкостями веществ в интервале температур от 298 до 500 К. (-673,29 кДж) Стандартная энтальпия образования формальдегида при 25С равна –108,6 кДж/моль. Рассчитайте стандартную энтальпию образования формальдегида при 150С, если известны теплоемкости: (-110,7 кДж моль-1)
Глава3. Второй закон термодинамики 3.1 Вопросы и упражнения Приведите несколько формулировок второго закона термодинамики и напишите его математическое выражение. Что такое к.п.д.? Почему его значение всегда меньше единицы? В чем состоит значение второго закона термодинамики для физической химии и химической технологии? В отличие от первого закона термодинамики второй закон носит статистический (вероятностный) характер. Что это означает? Что такое свободная и связанная энергия? Что такое энтропия? Как будет изменятся энтропия воды при ее переходе из твердого состояния в жидкое и из жидкого в газообразное? Почему энтропия системы всегда больше нуля? Напишите уравнение изменения энтропии для изотермических обратимых неизолированных, обратимых изолированных и изолированных необратимых процессов. В чем состоит физический смысл изобарно-изотермического и изохорно-изотермического потенциалов? Напишите уравнения, показывающие связь между термодинамическими потенциалами и другими термодинамическими функциями. Что показывает знак и величина изобарно-изотермического потенциала? Определите, какие из нижеприведенных реакций будут протекать в прямом, а какие – в обратном направлении. Какая из этих реакций будет ближе всего к равновесию в момент смешения эквимолярных количеств всех веществ, участвующих в реакции, а какая – дальше всего? Все вещества газообразные, температура и давление постоянны.
3.2 Примеры Пример 3-1 Рассчитайте изменение энтропии при нагревании 0,4 моль хлорида натрия от 20 до 850С. Мольная теплоемкость хлорида натрия равна: Ср(NaCl(тв)) = 45,94 +16,3210-3Т ДжК-1моль-1, Ср(NaCl(ж)) = 66,53 ДжК-1моль-1. Температура плавления хлорида натрия 800С, теплота плавления 31,0 кДжмоль-1. Решение: Общее изменение энтропии складывается из трех составляющих: нагревание твердого хлорида натрия от 20 до 800С, плавление, нагревание жидкого хлорида натрия от 800 до 850С. S1 = 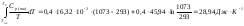 S2 = 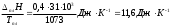 S3 = 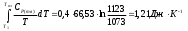 S = S1 + S2 + S3, S = (28,94 + 11,6 + 1,21) ДжК-1 = 41,75 ДжК-1 Ответ: 41,75 ДжК-1 Пример 3-2 Найдите изменение энтропии газа и окружающей среды, если n молей идеального газа расширяются от объема V1 до объема V2: А) обратимо, Б) против внешнего давления р. Решение: А) изменение энтропии газа при обратимом изотермическом расширении можно найти с помощью термодинамического определения энтропии с расчетом теплоты расширения по первому закону: Sr = Qобр/T = nRlnV2/V1. Т.к. расширение обратимое, то общее изменение энтропии Вселенной равно 0, поэтому изменение энтропии окружающей среды равно изменению энтропии газа с обратным знаком: Sокр = -Sr = -n RlnV2/V1. Б) Изменение энтропии газа при необратимом расширении против внешнего давления будет таким же, как и при обратимом расширении. Другое дело – энтропия окружающей среды, которую можно найти, рассчитав с помощью первого закона теплоту, переданную системе: Sокр = Qокр/T = - W/Т = р(V1 – V2)/Т. В этом выводе использован тот факт, что U = 0 (т.к.температура постоянна). Работа, совершаемая системой против постоянного давления, равна: W = р(V2 – V1), а теплота, принятая окружающей средой, равна работе, совершенной системой, с обратным знаком. Общее изменение энтропии газа и окружающей среды больше 0: S = n RlnV2/V2 + р(V1 – V2)/Т 0 как и полагается для необратимого процесса. Пример 3-3 Рассчитайте изменение энтропии 1000 г метанола в результате его замерзания при -105С. Теплота плавления твердого метанола при -98С равна 3160 Джмоль-1. Теплоемкость твердого и жидкого метанола равны 55,6 и 81,6 ДжК-1моль-1, соответственно. Решение: Необратимый процесс кристаллизации метанола при температуре -105С можно представить в виде последовательных обратимых процессов: А) нагревание метанола от –105С до температуры кристаллизации (-98С), Б) кристаллизация метанола при -98С, В) охлаждение метанола от -98С до -105С: 1 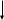  75 К ж 2 тв 75 К ж 2 тв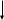 1 3 1 31  68 К ж ? тв 68 К ж ? твИзменение энтропии в первом и в третьем процессах (при изменении температуры) рассчитывается по формуле: S1 = nCр(Ж)lnT2/Т1, где n = m/М, S1 = (1000/32)81,6ln175/168 ДжК-1 = 104,10 ДжК-1, S3 = (m/М)Cр(тв)lnT2/Т1, S3 = (1000/32)55,6 ln168/175 ДжК-1 = -70,93 ДжК-1. Изменение энтропии во втором процессе рассчитывается как для обычного фазового перехода, учитывая, что теплота при кристаллизации выделяется: S2 = крН/Ткр, S2 = -(1000/32)3160/175 ДжК-1 = -564,29 ДжК-1. Общее изменение энтропии равно сумме по этим трем процессам: S = S1 + S2 + S3, S = (104,10 - 564,29 – 70,93) ДжК-1 = = -531,12 ДжК-1. Ответ: -531,12 ДжК-1. Пример 3-4Рассчитайте изменение энтропии при смешении моля водорода с 1 моль азота при давлении 1,013105 Па и постоянной температуре. Решение: При смешении газы будут диффундировать друг в друга. При данных условиях газы можно принять за идеальные. Поэтому общее изменение энтропии при смешении газов будет равно сумме изменений энтропий каждого газа при его расширении до объема смеси. Т.к. процесс изотермический, то для каждого газа: S = nRlnV2/V1. V = nRT/р, VH2 = VN2 SN2 = SH2 = nRln2 = 18,314ln2 Дж/К = 5,763 Дж/К S = SH2 + SN2, S = (5,763 + 5,763) Дж/К = 11,526 Дж/К. Ответ: 11,526 Дж/К. 3.3 Задачи 3-1. Рассчитайте изменение энтропии при нагревании 0,7 моль моноклинной серы от 25 до 200С при давлении 1 атм. Мольная теплоемкость серы равна: Ср(S(тв)) = 23,64 ДжК-1моль-1, Ср(S(ж)) = (35,73 + 1,1710-3Т) ДжК-1моль-1. Температура плавления моноклинной серы 119С, удельная теплота плавления 45,2 Джг-1. (11,88 ДжК-1) 3-2. Один килограмм воды, взятой при 0С, переведен в состояние перегретого пара с температурой 200С и давлении 1,013105Па. Вычислите изменение энтропии этого перехода, если удельная теплота испарения воды при 100С равна 2257 Дж/г, удельная теплоемкость водяного пара при давлении в 1,013105Па равна 1,968 ДжК-1моль-1. (7824,8 Дж) 3-3. Под давлением 19,6104 Па нагревают 210-3 м3 аргона до тех пор, пока объем его не увеличится до 1210-3 м3. Каково изменение энтропии, если начальная температура 373 К. (2,44 ДжК-1моль-1) 3-4. Вычислите изменение энтропии при нагревании 16 кг О2 от 273 до 373 К при постоянном объеме. Считайте кислород идеальным газом.(3242,46 ДжК-1) 3-5. 3,00 моль газообразного СО2 расширяются изотермически (в тепловом контакте с окружающей средой, имеющей температуру 15,0С) против постоянного внешнего давления 1,00 бар. Начальный и конечный объемы газа равны 10,0 л и 30,0 л, соответственно. Рассчитайте изменение энтропии: а) системы, считая СО2 идеальным газом, б) окружающей среды, в) Вселенной. (Sсист=27,4ДжК-1,Sокр = -6,94ДжК-1, Sвсел=20,46ДжК-1) 3-6. Найдите изменение энтропии газа газа и окружающей среды, если n молей идеального газа расширяются изотермически от давления р1 до давления р2: а) обратимо; б) против внешнего давления р р2. (а) Sгаз = nRln(p1/p2), Sокр = -nRln(p1/p2), б) Sгаз = nRln(p1/p2), Sокр = nRр(1/p1 - 1/p2)) 3-7. Рассчитайте изменение энтропии 1000 г воды в результате ее замерзания при -5С. Теплота плавления льда при 0С равна 6008 Джмоль-1. Теплоемкость льда и воды равны 34,7 и 75,3 ДжК-1моль-1, соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс самопроизвольный. (-1181Дж/К) 3-8. Вычислите изменение энтропии в процессе затвердения 1 моль переохлажденного бензола при 268 К, если при 278 К Нпл (бензола)=9956Джмоль-1,Ср бензола(ж)=127,3ДжК-1моль-1, Ср бензола(тв) = 123,6 ДжК-1моль-1, Р = cоnst = 1,01105 Па. (35,61 ДжК-1моль-1) 3-9. Определите изменение энтропии, если 10010-3 кг воды, взятой при 273 К, превращается в пар при390 К. Удельная теплота испарения воды при 373 К равна 2263,810-3 Джкг-1; удельная теплоемкость жидкой воды 4,2 Джкг-1К-1; удельная теплоемкость пара при постоянном давлении 2,010-3 Джкг-1К-1. (142 ДжК-1моль-1) 3-10. Азот (0,001 м3) смешан с 0,002 м3 кислорода при 27С и давлении 1,013105 Па. Найти общее изменение энтропии системы. (0,645 Дж) 3-11. В двух сообщающихся сосудах, разделенных перегородкой, находятся 1 моль азота и 2 моль кислорода. Перегородку вынимают, газы смешиваются. Рассчитайте общее изменение энтропии, если исходные температуры и давления одинаковы, а объемы различны; VN2 = 1 л, VO2 = 2 л. Конечное давление смеси равно исходному давлению газа. (15,876 ДжК-1моль-1) 3-12. В двух сосудах одинаковой емкости находится: в первом 2,8 г азота, во втором 4 г аргона. Определите изменение энтропии при диффузии, возникающей в результате соединения сосудов с газами. Температура и давление постоянны. (1,15 Дж) 3-13. Смешали 1 моль аргона, взятого при TAr = 293 К, с 2 моль азота, взятого при ТN2 = 323 К. Исходные давления компонентов и конечное давление смеси одинаковы. Вычислите температурную составляющую энтропии смешения. Теплоемкость аргона равна 20,8 ДжК-1моль-1 и азота 29,4 ДжК-1моль-1. (0,033 ДжК-1моль-1) Глава 4. Термодинамические потенциалы 4.1 Примеры Пример 4-1 Два моля гелия (идеальный газ, мольная теплоемкость Ср = 5/2R) нагревают от 100 до 200С при р = 1 атм. Вычислите изменение энергии Гиббса в этом процессе, если известно значение энтропии гелия, S373 = 131,7 ДжК-1моль-1. Можно ли считать этот процесс самопроизвольным? Решение: Изменение энергии Гиббса при нагревании от 373 до 473 К можно найти, проинтегрировав частную производную по температуре: 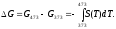 Зависимость энтропии от температуры при постоянном давлении определяется изобарной теплоемкостью: 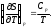 Интегрирование этого выражения от 373 К до Т дает: 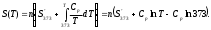 Подставляя это выражение в интеграл от энтропии, находим: 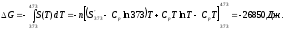 Процесс нагревания не обязан быть самопроизвольный, т.к. уменьшение энергии Гиббса служит критерием самопроизвольного протекания процесса только при Т = const и р = const. Ответ: -26850 Дж. Пример 4-2 Рассчитайте изменение энергии Гиббса в реакции: СО + 1/2О2 = СО2 при температуре 500 К и парциальных давлениях 3 бар. Будет ли эта реакция самопроизвольной при данных условиях? Газы считать идеальными. Необходимые данные возьмите из справочника. Решение: Термодинамические данные при температуре 298 К и стандартном давлении 1 бар сведем в таблицу:
Примем, что rСp = соnst. Изменения термодинамических функций в результате реакций рассчитаны как разность функций реагентов и продуктов: f = f(СО2) - f(СО) – 1/2 f(О2). Стандартный тепловой эффект реакции при 500 К можно рассчитать по уравнению Кирхгофа в интегральной форме: 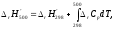 rН500 = -283000 + (-9,27)(500 – 298) = -284,9 кДжмоль-1 Стандартное изменение энтропии в реакции при 500 К можно рассчитать по формуле: 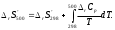 rS500=(-86,4+(-9,27)ln(500/298))ДжК-1моль-1= =-91,2ДжК-1моль-1 Стандартное изменение энергии Гиббса при 500 К: rG500 = rН500 - 500rS500, rG500 = (-284900 – 500(-91,2)) кДжмоль-1=-239,3кДжмоль-1. Рассчитаем изменение энергии Гиббса при парциальных давлениях 3 атм: 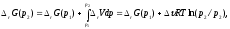 rG(р2) = - 240200 + (-0,5)8,31500ln(3) = -242,5 кДжмоль-1. Эта реакция может протекать самопроизвольно при данных условиях. Ответ: rG = -242,5 кДжмоль-1. 4.2 Задачи Вычислите изменение Н, U, F, G, S при одновременном охлаждении от 2000 К до 200 К и расширении от 0,5 м3 до 1,35 м3 0,7 молей азота (СV = 5/2R). Энтропия газа в исходном состоянии равна 213,4 ДжК-1моль-1, газ можно считать идеальным. (Н = -36,66 кДж, U = -26,19 кДж, F = 249,4 кДж, G = 238,9 кДж, S = -27,72 ДжК-1) Рассчитайте G при 25С для химической реакции: 4НСl(г) + О2(г) = 2Cl2 + 2Н2О(ж). Стандартные значения энтальпии образования и абсолютной энтропии при 25С равны: fН(НСl) = -22,1 ккалмоль-1, S(O2) = 49,0 калК-1моль-1, fН(Н2О(ж)) = -68,3 ккалмоль-1, S(Сl2) = 53,3 калК-1моль-1, S(НCl) = 44,6 калК-1моль-1, S(Н2O(ж)) = 49,0 калК-1моль-1. (G = -22,2 ккалмоль-1) Вычислите изменение энергии Гиббса при сжатии 0,710-2 кг N2 при 300 К и давлении от 5,05104 до 3,031105 Па (считать азот идеальным газом). Вычислите G298 для реакции С(графит) + 2Н2(г) = СН4(г). Определите Н298 из следующих термохимических уравнений: СН4(г) + 2О2(г) = СО2(г) + 2Н2О(ж) + Н298, СО2(г) = С(графит) + О2(г) - Н298, 2Н2О(ж) = 2Н2(г) + О2(г) - 2Н298. Значение S298 вычислите с помощью постулата Планка. Рассчитайте стандартные энергии Гиббса и Гельмгольца при 700С для химической реакции: СаСО3(тв) = СаО(тв) + СО2(г). Теплоемкости веществ считать постоянными. (rG973 = 24,4 кДжмоль-1, rF973 = 16,3 кДжмоль-1) Вычислите изменение G для 1 моль NН3 в процессе изобарического нагревания (Р = 1,013105 Па) от Т1 = 300 до Т2 = 400 К, если Ср = соnst. (-17,467 кДжК-1моль-1) Найдите энергию Гиббса образования NН3 при температурах 298 и 400 К, если известны следующие данные: fН298(NН3) = -46,2 кДжмоль-1,
Считать, что теплоемкости в указанном интервале температур постоянны. (fG298(NH3) = -16,7 кДжмоль-1, rG400(NH3) = -6,19 кДжмоль-1) Литература 1) Г.С. Каретников, И.В. Кудряшов. Сборник примеров и задач по физической химии. - М: Высшая школа, 1991 г. 2) И.И. Климов, А.И. Филько. Сборник примеров и задач по физической и коллоидной химии. – М: Просвещение, 1975 г. 3) В.В. Еремин, С.И. Каргов, И.А. Успенская, Н.Е. Кузьменко, В.В. Лунин. Основы физической химии. Теории и задачи. – М: Экзамен, 2005. |
