Физическая химия (1-15 вопросы). Дисциплина Физическая химия

• Название: Дисциплина Физическая химия
• Анкор: Физическая химия (1-15 вопросы).docx
• Дата: 08.04.2017
• Размер: 1.46 Mb.
• Имя файла: Физическая химия (1-15 вопросы).docx
• Тип: Закон; #4617
• страница: 1 из 5

Дисциплина: Физическая химия

1. Первой закон термодинамики, основные формулировки и математическое выражение первого закона термодинамики. Применение его к термодинамическим процессам. Работа расширения идеального газа в изохорном, изобарном, изотермическом и адиабатном процессах.

2. Теплоемкость. Виды теплоемкости. Связь между средней и истинной теплоемкостью. Теплоемкость при постоянном давлении и объеме и связь между ними. Температурная зависимость теплоемкости от температуры.

3. Закон Гесса и следствия из него. Применение первого закона термодинамики к химическим процессам. Связь между q_p и q_v. Расчет тепловых эффектов химических реакций по теплотам образования и теплотам сгорания веществ (на примере реакции).

4. Зависимость теплового эффекта от температуры. Уравнение Кирхгоффа в дифференциальной и интегральной форме.

5. Обратимые и необратимые, самопроизвольные и несамопроизвольные процессы. Второй закон термодинамики, его формулировки и математическое выражение. Цикл Карно.

6. Энтропия как мера неупорядоченности системы. Свободная и связанная энергия. Расчет изменения энтропии при различных термодинамических процессах и при протекании химических реакций.

7. Основные соотношения между термодинамическими функциями. Уравнение Гиббса-Гельмгольца.

8. Применение второго закона термодинамики к фазовым превращениям. Вывод дифференциальной формы уравнения Клаузиуса - Клапейрона для процесса кипения. Интегрирование уравнения Клаузиуса - Клапейрона и его анализ.

9. Химическое равновесие. Классификация равновесных состояний. Признаки равновесных состояний. Закон действующих масс. Вывод константы равновесия для гомогенной реакции. Связь между различными формами выражения констант равновесия.

10. Химическое равновесие в гетерогенных системах. Расчет константы равновесия. Химическое сродство как мера реакционноспособности системы. Изотерма Вант-Гоффа. Нормальное химическое сродство.

11. Зависимость константы равновесия от температуры. Уравнение изобары Вант-Гоффа в дифференциальной и интегральной формах. Зависимость константы равновесия от температуры. Уравнение изохоры Вант-Гоффа в дифференциальной и интегральной формах.

12. Расчет равновесных состояний с помощью таблиц стандартных термодинамических величин и по методу Тёмкина-Шварцмана

13. Термодинамика и законы разбавленных растворов. Понижение давления пара растворителя над раствором. Закон Рауля.

14. Растворимость газов в жидкостях. Закон Генри. Зависимость растворимости газов от различных факторов.

15. Замерзание и кипение растворов. Криоскопия и эбуллиоскопия.

16. Закон распределения. Экстракция.

17. Химический потенциал и общие условия равновесия системы.

18. Термодинамика и законы реальных растворов. Положительные и отрицательные отклонения от закона Рауля. Перегонка. Законы Коновалова.

19. Диаграмма состояния однокомпонентных систем Диаграммы состояния воды .

20. Термический анализ. Построение диаграмм состояния по кривым охлаждения. Анализ диаграмм состояния по конноде и по правилу фаз Гиббса. Анализ диаграмм состояния двухкомпонентных систем с неограниченной растворимостью в твердом и жидком состоянии.

21. Анализ трехкомпонентных систем. Объемные и плоские диаграммы состояния трехкомпонентных систем. Треугольники концентраций. Определение концентраций по методам Гиббса и Розебома.

22. Теория электролитической диссоциация. Степень диссоциации. Изотонический коэффициент. Закон Оствальда.

23. Электролиты. Электролитическая проводимость растворов электролитов: удельная и эквивалентная. Зависимость этих электропроводностей от концентрации.

24. Гальванические элементы. Механизм возникновения электродного потенциала. Строение двойного электрического слоя. Вывод уравнения Нернста. Элемент Якоби-Даниэля.

25. Измерение электродвижущие силы гальванического элемента. Классификация электродов. Типы электродов. Электроды первого, второго и третьего рода. Электроды сравнения.

26. Кинетика химических реакций. Задачи кинетики. Понятие о скорости. Виды скорости. Молекулярность и порядок реакций.

27. Кинетика простых реакций. Вывод кинетического уравнения для реакции первого, второго и третьего порядка. Период полураспада.

28. Порядок реакции. Методы определения порядка реакции.

29. Зависимость скорости реакции от температуры. Правило Вант-Гоффа. Энергия активации и методы её определения.

30. Теория активных столкновений Аррениуса.

1. Первой закон термодинамики, основные формулировки и математическое выражение первого закона термодинамики. Применение его к термодинамическим процессам. Работа расширения идеального газа в изохорном, изобарном, изотермическом и адиабатном процессах.

Содержание и формулировки первого закона термодинамики

Первый закон («первое начало») термодинамики есть частный случай закона сохранения и превращения энергии применительно к процессам, которые сопровождаются выделением, поглощением или преобразованием теплоты. Первый закон был обоснован работами Гесса (1836), Джоуля (1840), Майера (1842), Гельмгольца (1847) и др. Наиболее обычными формулировками первого закона термодинамики являются следующие:

• 
  энергия, полученная системой в форме теплоты, может превращаться в работу и, наоборот, полученная в форме работы - в теплоту; если по окончании превращений система возвращается в исходное состояние, то теплота и работа равны друг другу, независимо от характера процесса (Гельмгольц): W= Q;
  
• 
  вечный двигатель первого рода невозможен, т. е. невозможно построить машину, которая совершала бы механическую работу, не затрачивая на это соответствующего количества энергии (Оствальд);
  
• 
  в любой изолированной системе запас энергии остается постоянным (Джоуль):U= const,dU= 0.
  

Математическое выражение первого закона термодинамики

Взаимосвязь между внутренней энергией, работой и теплотой устанавливается на основе первого закона термодинамики.

Изменение внутренней энергии системы ΔUможет происходить за счет обмена теплотой Q и работой А с окружающей средой. В термодинамике условились считать положительными величинами теплоту, полученную системой, и работу, совершенную системой.

Тогда из формулировки первого закона термодинамики следует, что теплота, полученная системой извне, расходуется на приращение внутренней энергии и работу, совершенную системой, т. е.

_{Q = ΔU+W.}

Если эти количества бесконечно малы, то закон записывается в дифференциальной форме: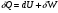

,

где dU- полный дифференциал внутренней энергии системы; δQи δW- бесконечно малые количества теплоты и работы.
Применение закона к термодинамическим процессам

Изотермический процесс (Т=соnst) в идеальном газе силы межмолекулярного взаимодействия равны нулю. Внутренняя энергия идеального газа зависит от температуры, количества вещества и не зависит от давления и объема, поэтому для данных условий U=соnst; dU=0, dQ_Т=р·dV ; QТ=W теплота, сообщенная системе, в изотермическом процессе полностью расходуется на совершение работы расширения. используя р=RТ/V и проинтегрировав получим W= RТln(V₂/V₁) = RТln(Р₁/Р₂), т.к. по закону Бойля-Мариотта (РV)Т = соnst

Изохорный процесс (V= соnst) при постоянном объеме dV=0, значит работа расширения газа dW= рdV=0 и dQ V = dU или Q = U₂- U₁ =dd U

В изохорном процессе теплота, сообщенная системе, полностью расходуется на увеличение ее внутренней энергии и характеризует изменение состояния системы.

Изобарный процесс (р= соnst) постоянную величину р можно внести под знак дифференциала, поэтому работа расширения dW = рdV =dW = d(рV) и dQр=dU+d(рV) = d(U +рV)= ΔН

Работа расширения идеальных газов

Идеальный газ – это газ для идеализированной системы, состоящей из частиц, собственный объем которых мал по сравнению со всем объемом системы, и которые находятся в непрерывном хаотическом движении.

Работу принято считать положительной (А > 0), если система производит её над окружающей средой. Различают работу: механическую, поверхностных сил, электрическую и т. п. Механическую работу под действием сил давления называют работой расширения.

Выясним, какое количество работы совершит газ при расширении.

Рассмотрим обратимое расширение газа в цилиндре постоянного сечения S.

Обозначим: р- внешнее давление; dh- бесконечно малое смещение поршня.

dh

S р^